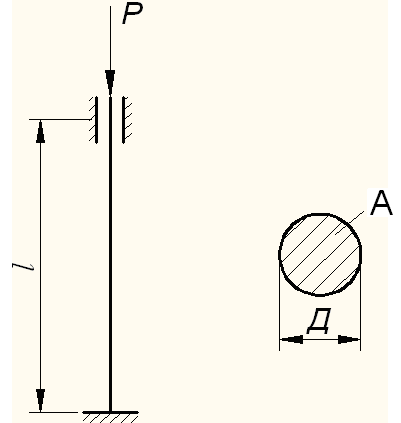
8. Сығылған түзу стержендерді орнықтылыққа есептеу

Тапсырма шарты: Берілген Р күшінің әсерінен центрлік сығылған болат стерженнің көлденең қимасының өлшемдерін анықтау.

Есептің схемасын 24 суреттен, ал сандық мәндерін 6 кестеден алу керек.

Кесте 6 - №7 есептеп-жобалау жұмысының сандық мәндері

Нұсқалар
		м
1-18	10	1	0,90	1,10	1,10	0,9
19-36	11	1,1	0,35	1,15	1,15	0,85
37-54	12	1,2	0,80	1,20	1,20	0,8
55-72	13	1,3	0,75	1,25	1,25	0,75
73-90	14	1,4	0,70	1,30	1,30	0,70
91-108	15	1,5	0,65	1,35	1,35	0,65
109-126	16	1,6	0,60	1,40	1,40	0,60
127-144	17	1,7	0,55	1,50	1,50	0,55
145-162	18	1,8	0,50	1,55	1,55	0,50
163-180	19	1,9	0,45	1,55	1,60	0,45
181-198	20	2,0	0,40	1,60	1,70	0,40
199-216	21	2,1	0,35	1,65	1,75	0,35
217-234	22	2,2	0,30	1,70	1,80	0,30

Талап етіледі:

1. Бірінші жақындау кезінде негізгі мүмкіндік кернеуді кемітуші коэффициенті φ_1б = 0,5 тең деп қабылдаймыз.

2. Стерженнің иілгіштігін анықтау және соған сәйкес φ_1к кестелік мәнін таңдау.

3. Кемітуші коэффициенттің берілген мәнін φ_1б кестелік мәнімен φ_1к салыстыру.

4. Кемітуші коэффициенттің берілген мәні φ_1б мен кестелік мәнінің φ_1к арасындағы айырмашылық 4-5 % болғанша қайталау.

Сурет 24 – №7 есептеп-жобалау жұмысының есептеу сұлбалары

24 суреттің жалғасы

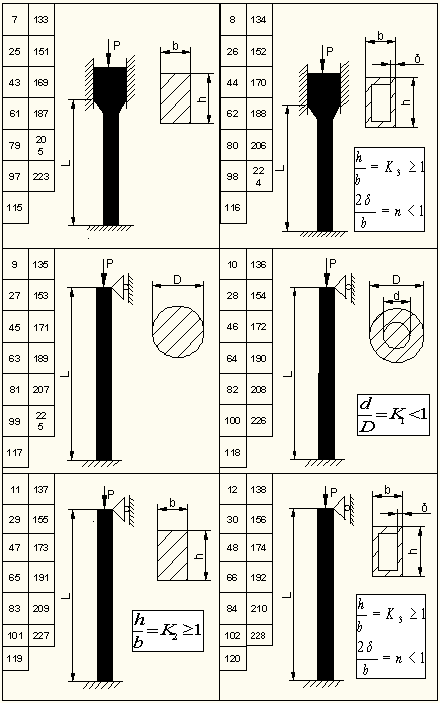
24 суреттің жалғасы

8.1 Есеп шығаруға арналған әдістемелік нұсқаулар

Сығылған түзу стержендерді орнықтылыққа тексергенде есептің екі түрі кездеседі: тура және кері. Егер стерженнің қимасының кескіні, ауданы, ұзындығы, материалы және оның бекітілу шарты берілсе, онда есеп тура деп аталады. Есептеу барысында күштің мүмкіндік мәні анықталады.

Егер есептеу кезінде қиманың ауданы белгісіз болса, онда есеп кері деп аталады.

Кері есепті шешу үшін графо-аналитикалық әдіс қолданылады.

Есепті шешу тәртібі:

1. Негізгі мүмкіндік кернеуді кемітуші коэффициентті тең деп қабылдаймыз

2. Стерженнің орнықтылық шартынан

(8.1)

Дөңгелек қима үшін , ал тік төртбұрыш немесе үшбұрыш үшін аудан шамалары қималардың қабырғаларының ұзындығы арқылы өрнектеледі.

Сондықтан (8.2)

Осыдан

(тік төртбұрыш және үшбұрыш үшін – анықталады )

3. Қиманың диаметрі (әлде ) арқылы оның инерция моментінің ең кіші мәні анықталады

(8.3)

4. Ең кіші инерция радиусы

(8.4)

(Тік төртбұрыш пен үшбұрыш үшін арқылы өрнектеу керек)

5. Стерженнің иілгіштігі

(8.5)

Мұндағы – тіректердің түрлеріне байланысты қабылданатын келтірілген ұзындық коэффициенті:

Кесте 7 - коэффициентінің мәндері

Тірек
	1
	2
	0,7
	0,5

6. Анықталған мәніне сәйкес кестеден мәні қабылданады. Болаттың маркалары сәйкес келетін коэффициентінің мәндері 8 кестеде келтірілген.

Кесте 8 - коэффициентінің мәндері

	0	10	20	30	40	50	60	70	80	90	100
	1,00	0,99	0,96	0,94	0,92	0,89	0,86	0,81	0,75	0,69	0,60

8 кестенің жаалғасы

	110	120	130	140	150	160	170	180	190	200
	0,52	0,45	0,40	0,36	0,32	0,29	0,26	0,23	0,21	0,19

Егер кестеден алынған мәні бастапқы қабылданған ден өзгеше болса,

(8.6)

деп қабылдап, есептеу жолын алынған және қабылданған мәндерінің теңескене дейін қайталаймыз.

Графо-аналитикалық әдіспен есептеуді келесі формулалардың көмегімен жүргіземіз:

Дөңгелек қима үшін

(8.7)

егер

(8.8)

егер

Өлшемдері в және h болатын тік төртбұрышты қима үшін, болғанда

(8.9)

егер

(8.10)

егер

2. Мысал

Тапсырма шарты. Екі ұшы қатаң бекітілген, P∙ =10кН күшпен сығылған болат стерженнің көлденен қима өлшемдерін анықтаңыз (25 сурет). Стержень ұзындығы ℓ=1м, негізгі мүмкіндік кернеу =160МПа=1600 кг/ , келтірілген ұзындық коэффициенті φ=0,5. P= кг,

Шешуі:

1. Алдымен деп қабылдаймыз, сонда

;

Осыдан

Дөңгелектің инерция моменті

Инерция радиусы

Стерженнің иілгіштігі

8 кестеден . Алынған бастапқы қабылданған φ=0,5- ке қарағанда айтарлықтай өзгеше.

Олай болса,

3. Есептеу жолын үшінші рет қайталаймыз

4. Есептеу жолын төртінші рет қайталаймыз

5. Есептеу жолын бесінші рет қайталаймыз

6. Есептеу жолын алтыншы рет қайталаймыз

болғанда , яғни . Сондықтан, стерженнің қимасының диаметрі ретінде мәнін қабылдаймыз.

8.7 формула бойынша стерженнің диаметрін анықтаймыз:

Осыдан, графо-аналитикалық әдістің аналитикалық бірте-бірте жақындау әдісіне қарағанда тиімді екенін көруге болады, өйткені есептеуге аз уақыт жұмсалады.