Предельные теоремы теории вероятностей

Есть две группы предельных теорем, объединяемых названиями: законы больших чисел (ЗБЧ) и центральная предельная теорема (ЦПТ). ЗБЧ устанавливают факт приближения среднего арифметического СВ к некоторой неслучайной величине (константе). ЦПТ устанавливает факт приближения ЗР суммы СВ к нормальному ЗР.

Прежде, чем переходить к рассмотрению предельных теорем, приведем ряд понятий и фактов,необходимых для их формулировки и доказательства.

Неравенство Чебышева

Получим вначале некоторые оценки для распределений СВ.

Лемма. Если неотрицательная СВ имеет конечное математическое ожидание , то для любого справедливо неравенство:

.

▲ Докажем лемму для НСВ (для ДСВ доказать самостоятельно). По определению математического ожидания НСВ

■.

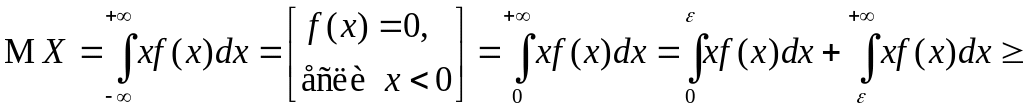
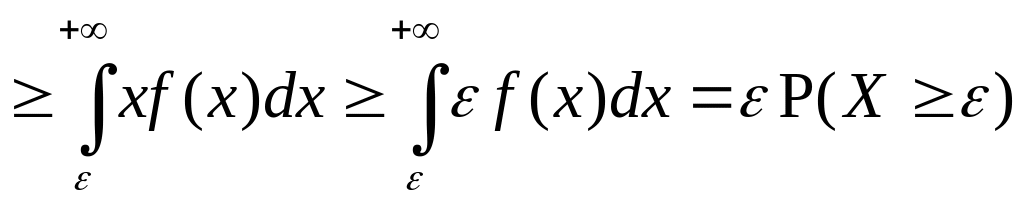Следствие (неравенство Чебышева). Если СВ имеет конечную дисперсию , то для любого справедливы следующие неравенства:

;(4.15)

.

▲В соответствии с леммой

,

что доказывает неравенство (4.15). Неравенство следует из (4.15) путем перехода к противоположному событию ■.

Неравенство Чебышева имеет большое теоретическое и практическое значение. Оно дает простую оценку для вероятности отклонения СВ с произвольным ЗР от ее математического ожидания. Причем, если о СВ, кроме ее математического ожидания и дисперсии ничего не известно, то эту оценку улучшить нельзя (существует пример СВ, для которой в (4.15) достигается равенство). Если же есть дополнительная информация о СВ (например, известен ее ЗР), то оценки (4.15) и могут быть существенно улучшены.

Пример. Пусть СВ имеет нормальный ЗР: . Тогда:

- на основании неравенства Чебышева

;

- в соответствии с «правилом »

,

где - функция Лапласа.

Виды сходимости последовательностей случайных величин и связь между ними

Определение. Говорят, что последовательность СВ сходится по вероятности к величине (случайной или нет), если для любого

или, что эквивалентно,

Краткое обозначение сходимости по вероятности: .

Определение. Говорят, что последовательность СВ сходится в среднем квадратическом к величине (случайной или нет), если

.

Краткое обозначение сходимости в среднем квадратическом: или (limitinthemean).

Лемма. Если последовательность СВ сходится к величине в среднем квадратическом, то она сходится к этой величине и по вероятности:

.

▲ В силу неравенства Чебышева

.

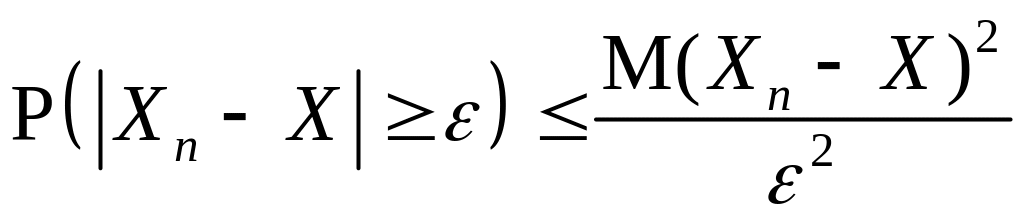Поэтому, если , то и, следовательно, для любого , поскольку вероятность не может быть отрицательной (лемма о двух милиционерах)■.

Смысл леммы: сходимость в среднем квадратическом является более сильной, чем сходимость по вероятности. Обратное неверно: из сходимости по вероятности сходимость в среднем квадратическом не следует.

Смысл введенных видов сходимостей последовательностей СВ: понятие предела определено только для числовой последовательности, поэтому случайность под знаком предела должна быть ликвидирована. Это делается либо с помощью вероятности, либо с помощью математического ожидания со своим понятием близости между и .