
- •010400 Информационные технологии
- •Часть 4
- •Функции случайных аргументов
- •Функции от случайных величин
- •Функции от случайных векторов
- •Композиция (свертка) законов распределения
- •Предельные теоремы теории вероятностей
- •Неравенство Чебышева
- •Виды сходимости последовательностей случайных величин и связь между ними
- •Законы больших чисел
- •Центральная предельная теорема
Самарский государственный аэрокосмический
университетимени академика С.П. Королева
Кафедра «Техническая кибернетика»
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Курс лекций
для студентов, обучающихся по направлению
010400 Информационные технологии
Часть 4
Функции случайныхаргументов.
Предельные теоремы
Лектор: к.ф.-м.н., доцент
Коломиец Э.И.
САМАРА 2012
Функции случайных аргументов
Пусть
![]() -
-
![]() ,
ЗР которого известен, и
,
ЗР которого известен, и
![]() - неслучайная функция (для простоты,
скалярная), область определения которой
содержит множество возможных значений
вектора
- неслучайная функция (для простоты,
скалярная), область определения которой
содержит множество возможных значений
вектора
![]() .
Рассмотрим СВ
.
Рассмотрим СВ
![]() .
Известно, что для нахождения числовых
характеристик СВ
достаточно знать только ЗР
.
Однако, во многих приложениях, особенно
в математической статистике, необходимо
уметь находить в явном виде ЗР СВ Y,
являющейся функцией случайных
аргументов.Рассмотрим вначале задачу
нахождения ЗР СВ Y
в одномерном случае (
.
Известно, что для нахождения числовых
характеристик СВ
достаточно знать только ЗР
.
Однако, во многих приложениях, особенно
в математической статистике, необходимо
уметь находить в явном виде ЗР СВ Y,
являющейся функцией случайных
аргументов.Рассмотрим вначале задачу
нахождения ЗР СВ Y
в одномерном случае (![]() ).
).
Функции от случайных величин
Дискретный
случай. Пусть
![]() – ДСВ, принимающая значения
– ДСВ, принимающая значения
![]() с вероятностями
с вероятностями
![]() (случай счетного числа значений СВ
рассмотреть
самостоятельно). Тогда для произвольной
неслучайной функции
(случай счетного числа значений СВ
рассмотреть
самостоятельно). Тогда для произвольной
неслучайной функции
![]() ,
область определения которой содержит
множество возможных значений СВ
,
СВ
,
область определения которой содержит
множество возможных значений СВ
,
СВ![]() является дискретной и задача состоит
в нахождении ее ЗР.
является дискретной и задача состоит
в нахождении ее ЗР.
а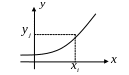 )
Предположим вначале, что все значения
)
Предположим вначале, что все значения
![]() различны (так, в частности, может быть,
если функция
различны (так, в частности, может быть,
если функция
![]() является монотонной в области возможных
значений случайной величины
).
Тогда случайная величина
будет иметь столько же возможных значений
является монотонной в области возможных
значений случайной величины
).
Тогда случайная величина
будет иметь столько же возможных значений
![]() ,
как и случайная величина
,
с
,
как и случайная величина
,
с
![]() и при этом
и при этом
![]() .
(4.1)
.
(4.1)
Таким образом, ЗР
СВ
![]() имеет вид:
имеет вид:
|
|
|
|
|
|
|
|
|
|
где в соответствии
с (4.1) вероятность
![]() .
.
б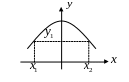 )
Предположим теперь, что среди значений
есть совпадающие (это может быть, в
частности, если функция
не является монотонной в области
в
)
Предположим теперь, что среди значений
есть совпадающие (это может быть, в
частности, если функция
не является монотонной в области
в озможных
значений случайной величины
).
Тогда случайная величина
будет иметь меньше возможных значений,
чем случайная величина
,
и ими являются
,
озможных
значений случайной величины
).
Тогда случайная величина
будет иметь меньше возможных значений,
чем случайная величина
,
и ими являются
,
![]() ,
различные среди
,
различные среди
![]() .
При этом вероятности
.
При этом вероятности
![]() значений
определяются по формуле:
значений
определяются по формуле:
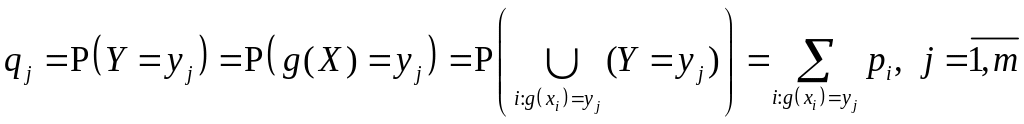 ,
(4.2)
,
(4.2)
ЗР СВ в данном случае имеет вид:
|
|
|
|
|
|
|
|
|
|
где в соответствии
с (4.2) вероятности
являются
суммой вероятностей![]() тех
значений
,
для которых
тех
значений
,
для которых
![]() .
.![]() ,
,
![]() .
.
Пример. Найти
ЗР СВ
![]() ,
если СВ Х является дискретной и
имеет ЗР
,
если СВ Х является дискретной и
имеет ЗР
|
-2 |
-1 |
0 |
1 |
2 |
|
0.2 |
0.2 |
0.2 |
0.2 |
0.2 |
Решение. В соответствии с (4.2) ЗР СВ имеет вид:
|
0 |
1 |
2 |
|
|
0.2 |
0.4 |
0.4 |
|
Непрерывный
случай. Если
– НСВ с ПВ
![]() ,
а
– дифференцируемая функция в области
возможных значений случайной величины
Х.Тогда
величина
является непрерывной СВ и задача состоит
в нахождение ПВ
,
а
– дифференцируемая функция в области
возможных значений случайной величины
Х.Тогда
величина
является непрерывной СВ и задача состоит
в нахождение ПВ![]() .
.
Предположим
вначале, что
- монотонно
возрастающая
функция в области возможных значений
СВХ.
Тогда у функции
существует однозначная обратная функция
![]() и
ФР СВ
можно записать в виде:
и
ФР СВ
можно записать в виде:
![]() .
.
Дифференцируя обе
части полученного равенства по
![]() ,
получаем:
,
получаем:
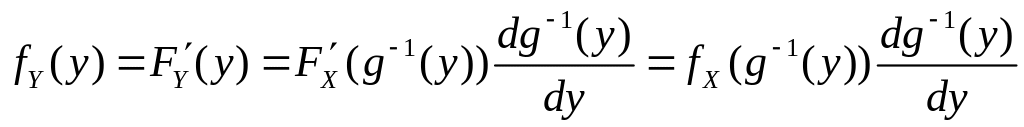 .
(4.3)
.
(4.3)
Для монотонно убывающейв области возможных значений СВ Хфункции
![]() ,
,
а после дифференцирования по обеих частей этого равенства
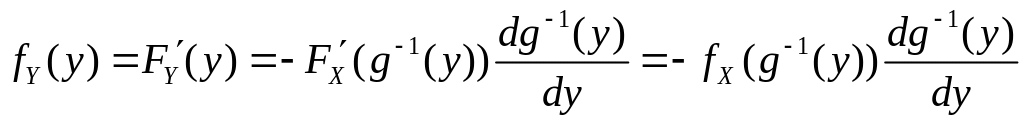 .
(4.4)
.
(4.4)
Объединяя полученные в (4.3) и (4.4) результаты, получаем:
Если – НСВ с ПВ , а – монотонная дифференцируемая функция, то СВ является непрерывной и ееПВ определяется через по формуле:
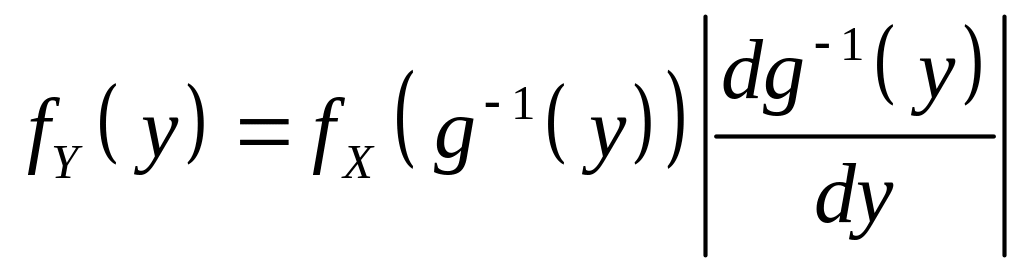 ,
(4.5)
,
(4.5)
где
![]() – функция, обратная к функции
– функция, обратная к функции
![]() (отметим, что равенство (4.5) имеет место
в точках непрерывности ПВ
и
).
(отметим, что равенство (4.5) имеет место
в точках непрерывности ПВ
и
).
Е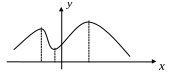 сли
дифференцируемая функция
не
является монотонной
в области
сли
дифференцируемая функция
не
является монотонной
в области
возможных значений
случайной величины
,
то ее область определения можно разбить
на
![]() непересекающихся интервалов, на каждом
из которых она монотонной будет и будет
иметь однозначную обратную функцию
непересекающихся интервалов, на каждом
из которых она монотонной будет и будет
иметь однозначную обратную функцию
![]() .
Применяя формулу (4.5) на каждом интервале
монотонности, получаем:
.
Применяя формулу (4.5) на каждом интервале
монотонности, получаем:
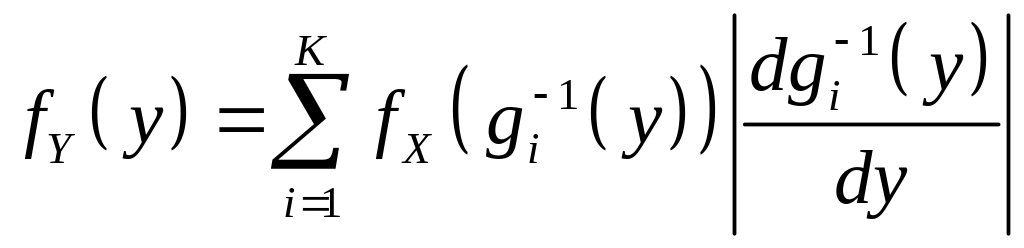 .
(4.6)
.
(4.6)
Пример 1.
Пусть
– НСВ с ПВ
,
а
![]() .
Найти ПВ
.
.
Найти ПВ
.
Решение.
В данном случае функция
![]() является монотонной при любых значениях
является монотонной при любых значениях
![]() (при
(при
![]() функция
возрастает, при
функция
возрастает, при
![]() - убывает). Функция, обратная к
,
имеет вид:
- убывает). Функция, обратная к
,
имеет вид:
![]() ,
а ее производная
,
а ее производная
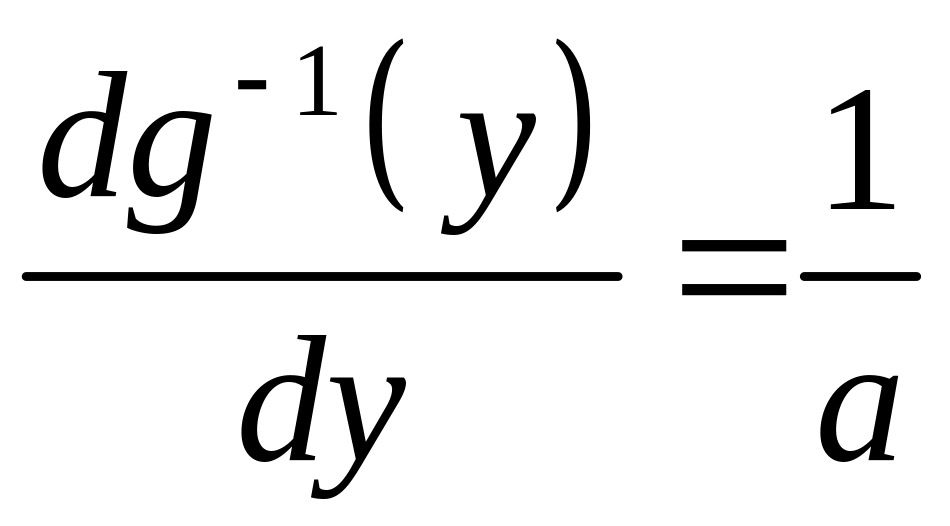 .
Поэтому в соответствии с (4.5)
.
Поэтому в соответствии с (4.5)
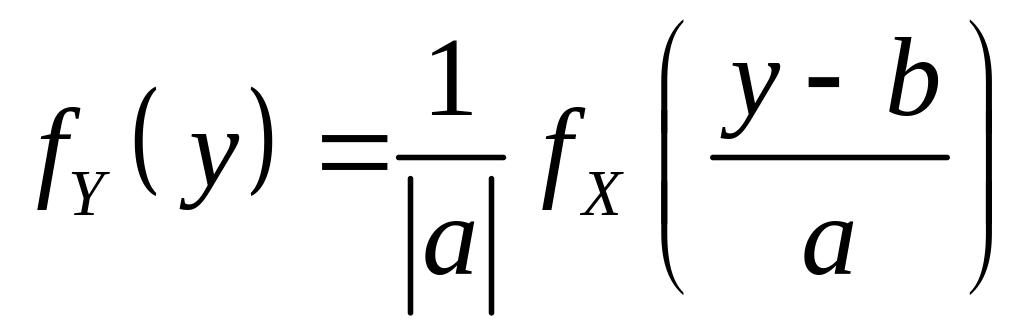 .
(4.7)
.
(4.7)
а) Рассмотрим
линейное преобразование вида
![]() над СВ
над СВ
![]() .
.
В соответствии с
(4.7) в этом случае
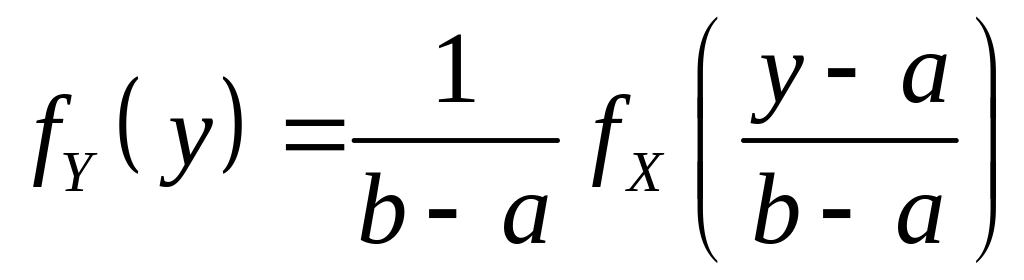 ,
а с учетом того, что
,
а с учетом того, что
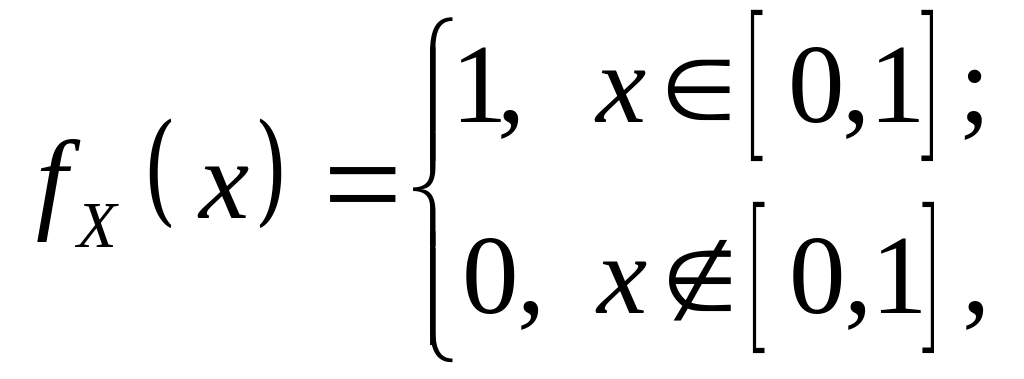
для ПВ СВ имеем выражение:
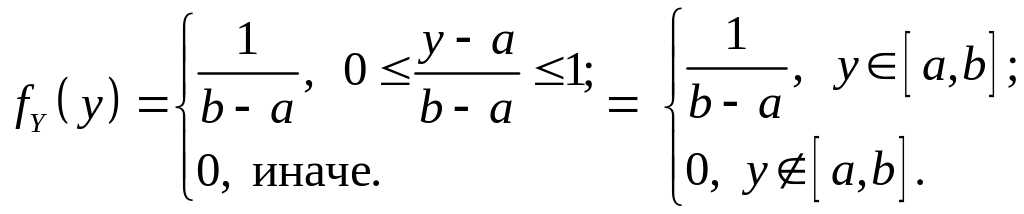
Полученный результат схематично можно записать
![]() .
.
и он означает, что
из равномерного распределения на отрезке
![]() можно получить равномерное распределение
на любом отрезке
можно получить равномерное распределение
на любом отрезке
![]() путем линейного преобразования.
путем линейного преобразования.
б) Рассмотрим
линейное преобразование вида
![]() над СВ
над СВ
![]() .
.
В соответствии с
(4.7) в этом случае
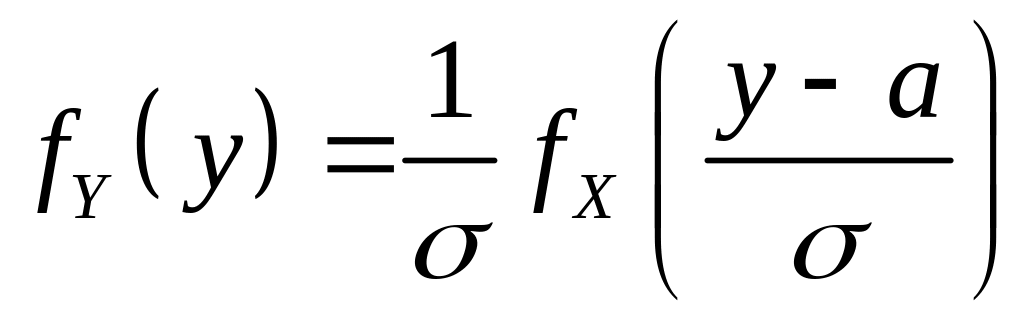 ,
а с учетом того, что
,
а с учетом того, что
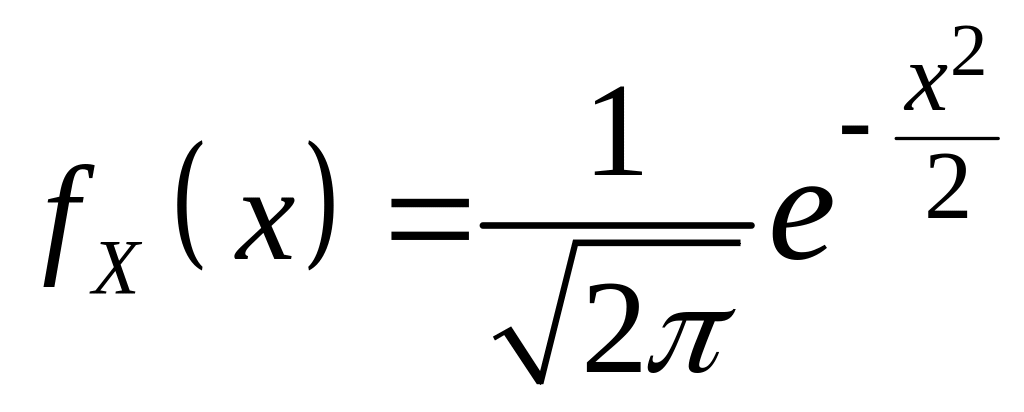
для ПВ СВ имеем выражение:
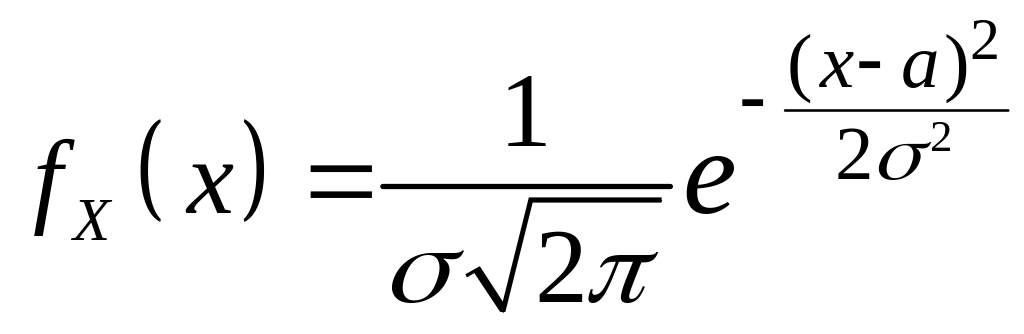 .
.
Полученный результат схематично можно записать
![]() .
.
и он означает, что
из стандартного нормального распределения
можно получить нормальное распределение
с любыми параметрами
![]() путем линейного преобразования.
путем линейного преобразования.
П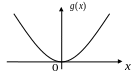 ример
2. Пусть
,
а
ример
2. Пусть
,
а
![]() .
Найти плотность вероятностей
.
.
Найти плотность вероятностей
.
Решение.
В данном случае функция
![]() не является монотонной в области
возможных значений случайной величины
и имеет два интервала монотонности
не является монотонной в области
возможных значений случайной величины
и имеет два интервала монотонности
![]() и
и
![]() .
На каждом из интервалов функция
имеет однозначную обратную функцию:
.
На каждом из интервалов функция
имеет однозначную обратную функцию:
![]() на первом интервале
и
на первом интервале
и
![]() - на втором
.
Поскольку модуль производной
- на втором
.
Поскольку модуль производной
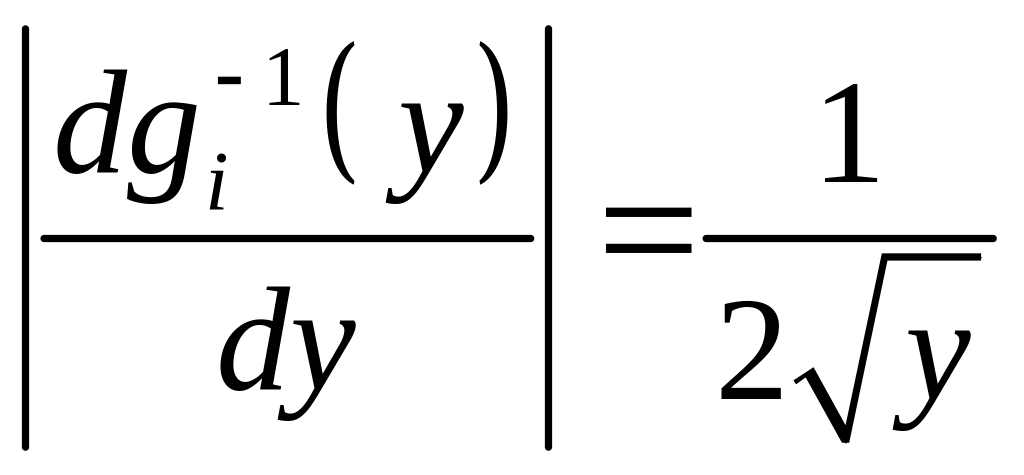 ,
,
![]() ,
то в соответствии с (4.6)
,
то в соответствии с (4.6)
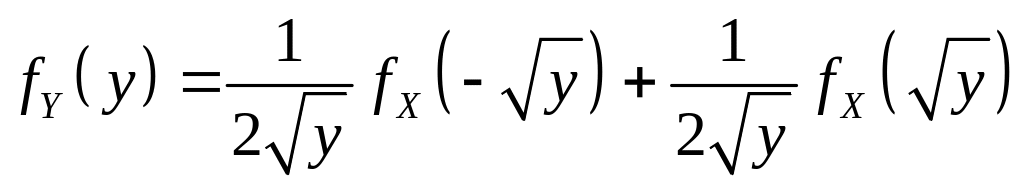 ,
,
а с учетом того,
что
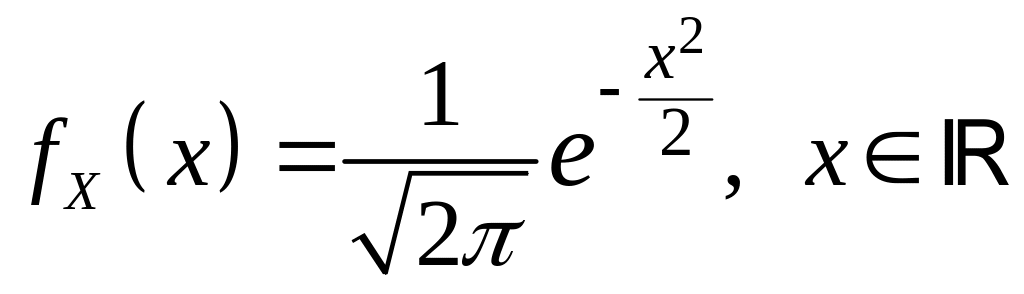 ,
получаем:
,
получаем:
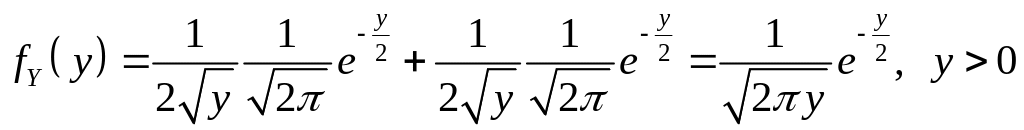 ,
,
![]() при
при
![]() .
.
Пример 3.
Пусть
![]() - строго монотонная ФР, а СВ
- строго монотонная ФР, а СВ
![]() .
Тогда СВ
.
Тогда СВ
![]() имеет заданную ФР
.
имеет заданную ФР
.
Решение. Действительно,
![]() .
.
Последнее равенство следует из того, что ФР СВ имеет вид:
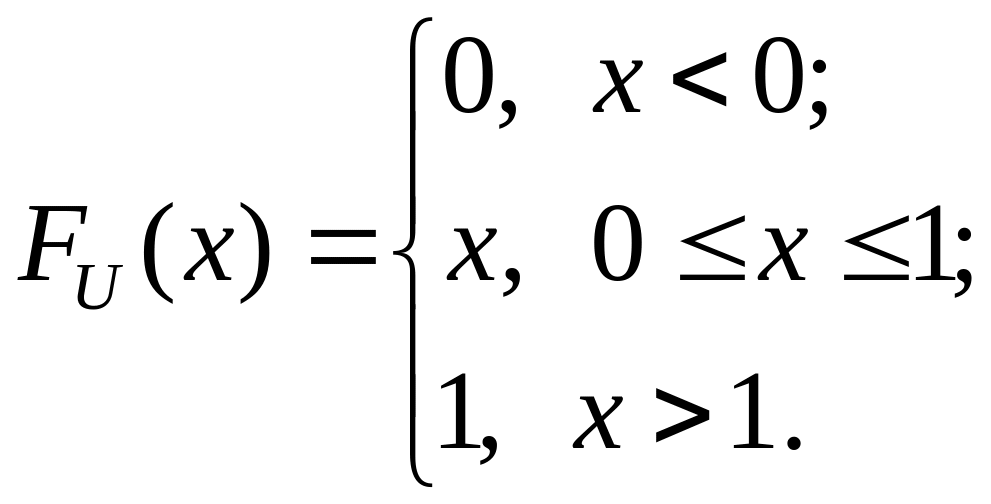 .
.
Смысл примера
3. Предположим,
что требуется получить
![]() значений
значений
![]() СВ
с заданным ЗР (смоделировать СВ
).
Для этого в соответствии с примером 3
необходимо найти ФР
СВ
с заданным ЗР (смоделировать СВ
).
Для этого в соответствии с примером 3
необходимо найти ФР
![]() СВ
и, если она имеет однозначную обратную
функцию, то положить
СВ
и, если она имеет однозначную обратную
функцию, то положить
![]() ,
,
,
,
где
![]() - значения СВ, имеющей равномерное
распределение на отрезке
(значения
можно
получитьпутем обращения к датчику
случайных чисел, входящему в стандартное
математическое обеспечение любого
персонального компьютера).
- значения СВ, имеющей равномерное
распределение на отрезке
(значения
можно
получитьпутем обращения к датчику
случайных чисел, входящему в стандартное
математическое обеспечение любого
персонального компьютера).
