Некоррелированность случайных величин и ее связь с независимостью

Определение. СВ и , для которых корреляционный момент , называются некоррелированными.

Учитывая, что

,

получаем: СВ и являются некоррелированными тогда и только тогда, когда .

Отсюда и из теоремы 2 вытекает, что из независимости СВ всегда следует их некоррелированность. Обратное, вообще говоря, неверно. Можно только сказать, что если СВ являются коррелированными, так, что , то они являются зависимыми.

Пример.

Равномерное распределение в круге .

Ранее были найдены одномерные ПВ координат вектора :

и установлено, что СВ и являются зависимыми, так как .

Найдем корреляционный момент СВ и .

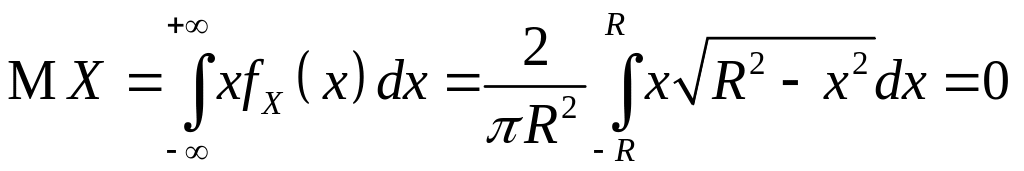
в силу нечетности подинтегральной функции и симметричности относительно нуля пределов интегрирования.

По аналогичным соображениям Найдем .

также в силу нечетности подинтегральной функции.

Таким образом, и, следовательно, СВ и являются зависимыми, но некоррелированными.

Понятие некоррелированности СВ играет важную роль в теории вероятностей. Подтверждением тому является следующая теорема.

Теорема 3 (теорема сложения дисперсий).

Для любых действительных чисел и любых СВ и , имеющих конечную дисперсию

.

В частности, если и СВ и являются некоррелированными, то имеет место свойство аддитивности дисперсии:

.

▲ Доказательство теоремы основано только на свойствах МО и определении корреляционного момента :

.■.

По индукции утверждение теоремы 3 обобщается на линейную комбинацию любого конечного числа СВ следующим образом.

Для любых действительных чисел и СВ , имеющих конечную дисперсию

.

В частности, если все , а СВ являются попарно некоррелированными ( ), то имеет место свойство аддитивности дисперсии:

.

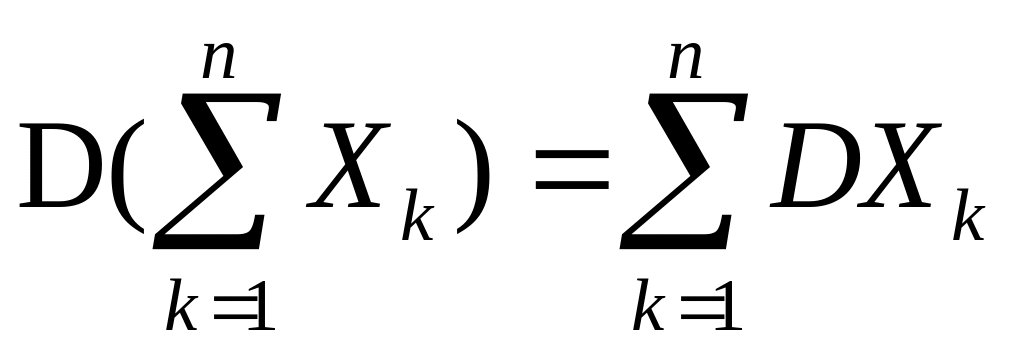Коэффициент корреляции его свойства

Значение корреляционного момента зависит от единиц измерения СВ и . Безразмерным аналогом является коэффициент корреляции, определяемый формулой:

,

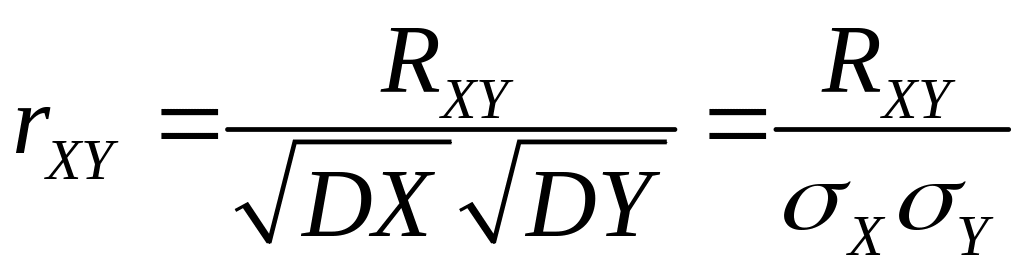где - средние квадратические отклонения СВ и .

Свойства коэффициента корреляции.

1. , если СВ и являются независимыми.

(Свойство очевидно, так как в этом случае ).

2. Коэффициент корреляции по модулю не превосходит 1: .

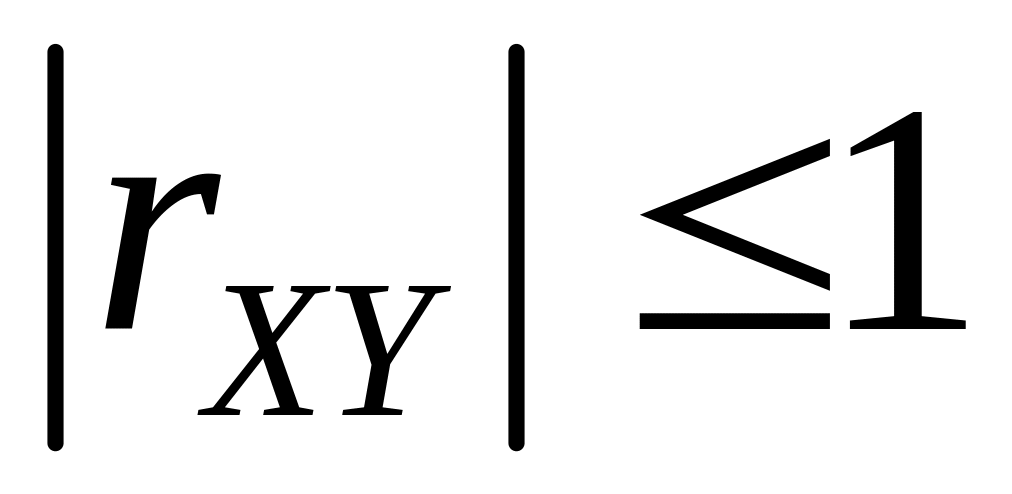▲ В соответствии со свойством 1 дисперсии

.

Положим . Тогда

,

откуда

.

Следовательно,

, или, эквивалентно, .■.

3. тогда и только тогда, когда СВ и связаны линейной зависимостью, то есть существуют действительные числа А и В такие, что .

▲ Необходимость. Предположим, что . Тогда и из доказательства свойства 2 коэффициента корреляции следует, что при . В соответствии со свойством 1 дисперсии это означает, что , откуда 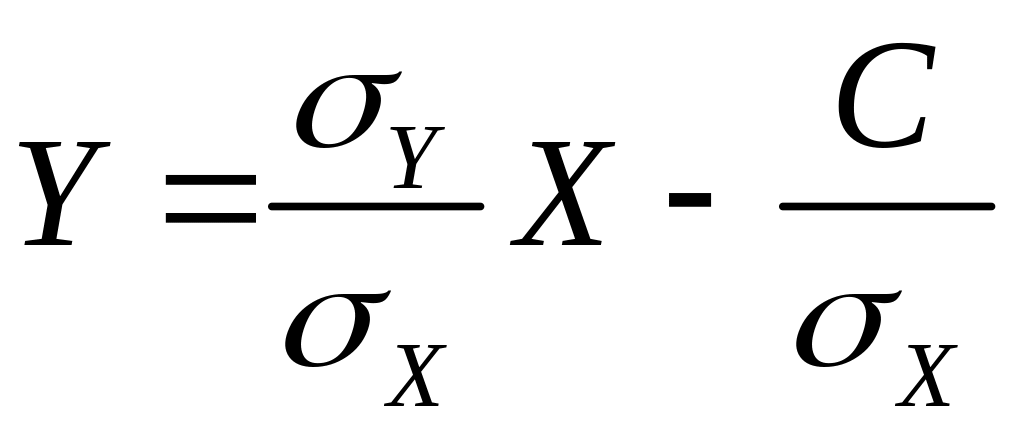и значит .

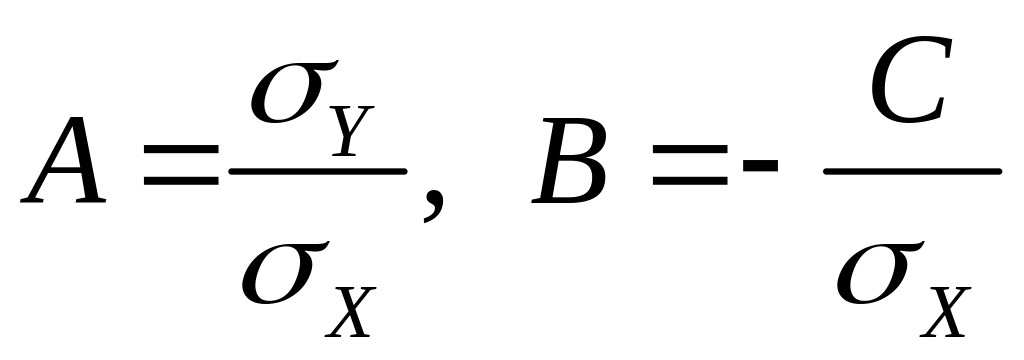Достаточность. Пусть . Тогда , а корреляционный момент СВ и равен

.

Поэтому ■.

Итак, для независимых СВ и достигает максимального по модулю значения для сильно (линейно) зависимых СВ. Поэтому значение коэффициента корреляции можно интерпретировать как степень линейной зависимости между СВ.

Г еометрическая иллюстрация: чем больше по модулю , тем плотнее значения располагаются вдоль некоторой прямой.

Многомерный случай.

Основными числовыми характеристики -мерного являются:

• математическое ожидание ;

• корреляционная матрица 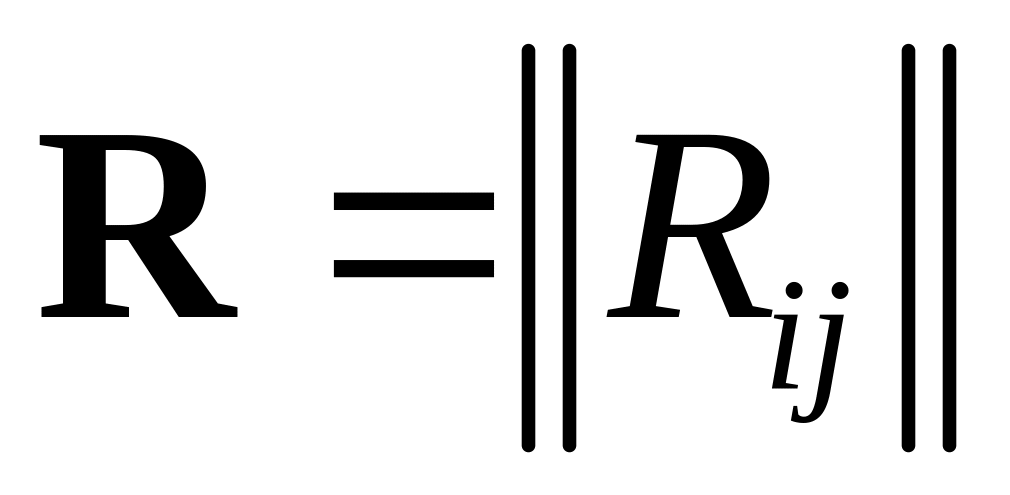, элементами которой являются всевозможные попарные корреляционные моменты координат: .

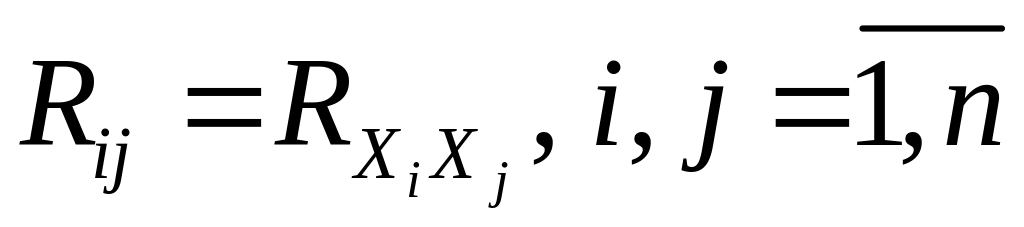Свойства корреляционной матрицы.

1. Матрица является симметрической размера : , .

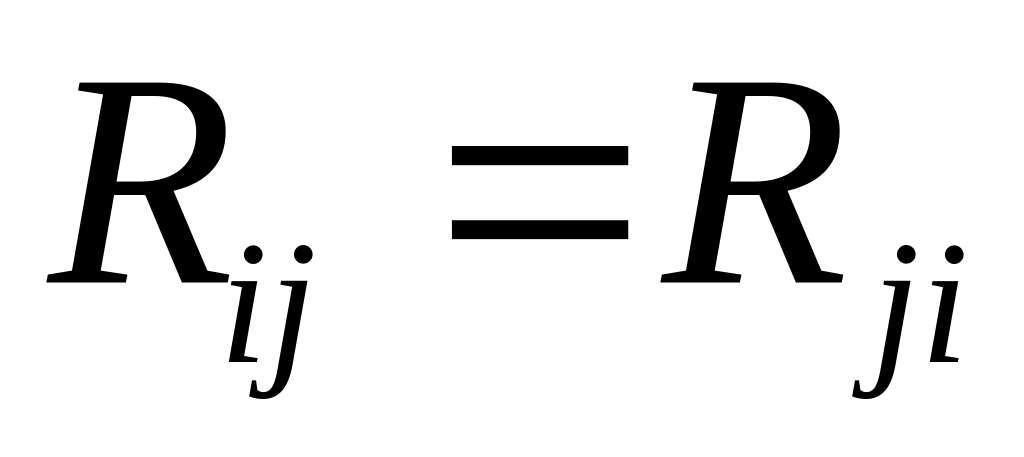2. На диагонали матрицы расположены дисперсии координат : , .

3. Матрица является неотрицательно определенной матрицей, то есть для любого и для любых действительных чисел

.

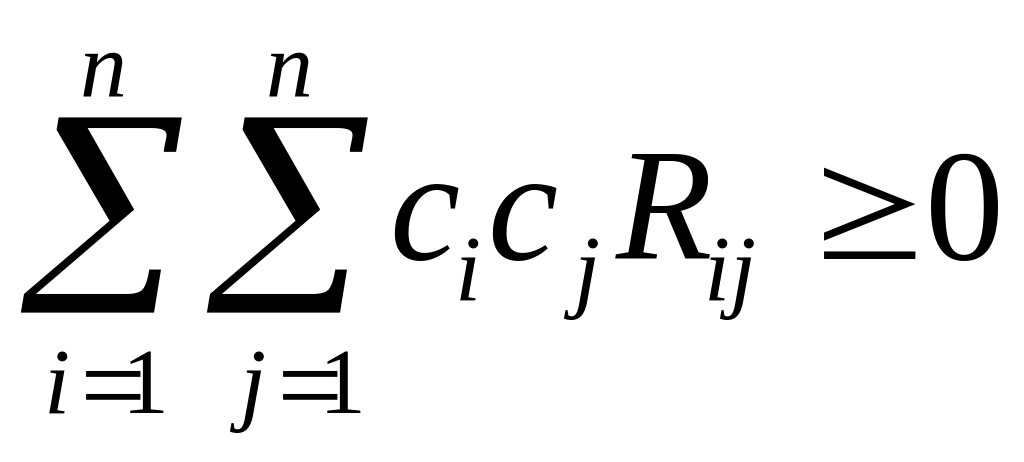▲ Обозначим - центрированную СВ, . Тогда и для произвольных чисел имеем:

■.

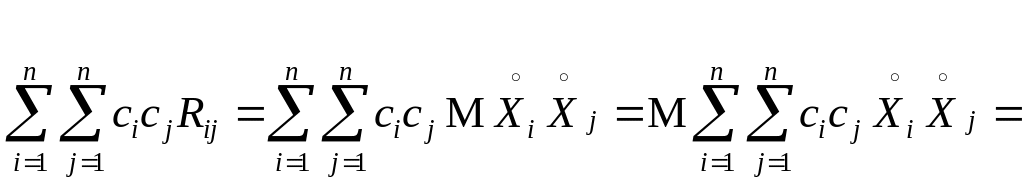
Наряду с корреляционной матрицей , иногда рассматривают нормированную корреляционную матрицу , элементами которой являются всевозможные попарные коэффициенты корреляции координат: . Отличие ее от просто корреляционной матрицы состоит в том, что у нормированной корреляционной матрицы все диагональные элементы равны 1: .