2.6 Котельников теоремасы

Шектелген жиілік жолағы бар сигналдарды Котельников қатары түрінде көрсету. Өзінің спектрі бойынша сигналды қайта қалпына келтіру үшін нөлден шексіздікке дейінгі аралықта жатқан жиіліктері бар құрастырушылардың барлығын ескеру қажет. Бірақ бұл процедура физикалық көзқарас жағынан тіпті мүмкін емес. Сонымен қатар спектралдық құрастырушылардың  -дағы үлесі сигналдардың энергиясының шектелгендігінен тіптен де кішкентай. Және де сигналдарды таратуға және өңдеуге арналған қандай да болмасын іс жүзіндегі құрылғының өткізу жолағының шекті ені бар.

Сондықтан, сигналдың мынандай қасиеті бар математикалық моделі шындыққа жанасатындай болады: тербелістің спектралдық тығыздығы шекті ұзақтылығы бар тек әлдебір жиіліктер жолағы шегінде нөлден өзгешеленеді. Радиотехникада осындай сигналды шектелген спектрі бар сигнал деп атайды.

Аналогтық (үздіксіз) сигналдан цифрлық сигналға көшкенде үш арнайы түрлендірулер іске асырылады: уақыт бойынша дискреттеу, амплитуда деңгейі бойынша кванттау және кодалау (цифрлау). Сигналдарды осылай түрлендіріп көрсету аналогты-цифрлық түрлендіру деп аталады.

Дискретизация деп үздіксіз сигналды уақыт бойынша дискретті есептемелер тізбегімен (әлдебір t = T уақыттық интервалымен жүретін таңдаулары бар) бейнелеуді (ауыстыруды) айтады және де олар бойынша белгілі бір дәлдікпен бастапқы сигналды қалпына келтіруге болады. Қарапайым түрде үздіксіз сигналды дискреттегенде оның белгілі уақыт аралығы t арқылы алынған сәйкесті амплитудадағы (шексіз қысқа импульстер түріндегі) есептемелік мәндерінің жиынтығы қалыптасады. Бұл жағдайда k- шы есептеменің амплитудасы үзіліссіз сигналдың t = k t уақыт сәтіндегі мәніне тең. Дискреттік есептемелерді цифрлық сигналдар түрінде бейнелеу (кодалау) үшін оларды алдын - ала кернеу деңгейі бойынша квантайды. Кванттау кезінде аналогтық сигналдың мүмкін болатын бүкіл амплитудалар өзгерістері диапазоны 0 ден Umax дейін (немесе әртүрлі полярлы сигнал жағдайында Umin-нан Umax –ға дейін) кернеудің бірдей немесе әртүрлі бекітіл-ген , кванттау адымы Δ деп аталатын, деңгейлеріне бөлшектенеді. Бірқалыпты

(Δ – тұрақты шама) және бірқалыпты емес (Δ-айнымалы шама) кванттау деп айырады. Бірқалыпты емес кванттау сирек қолданылады. Жалпы түрде кванттау процесі мына теңдеумен сипатталады

(2.27)

мұнда -квантталған сигнал; - кванттар саны, -бірлік функция.

Біркелкі кванттағанда U_k(t) сигналдың әрбір бекітілген деңгейіне

шартты сан, цифрлық кода түрінде анықталған мән беріледі. Техникалық жағынан іске асыру мен өңдеу ыңғайлылығы жағынан қарағанда әдетте N (N — бүтін нақты сан ) разрядтардан тұратын, әрқайсысы «1» - импульстан немесе «0» -паузадан тұратын екілік цифрлық кодаларды пайдаланады. Кванттау деңгейлерінің жалпы саны болатыны айдан анық. Кванттаудың бір адымы шамасы екілік коданың разрядтар санымен келесі өрнекпен байланысқан:

(2.28)

Цифрлық техникада, разрядтық импульстары мен паузалары уақыттық аралықсыз дискреттеудің Δt бір интервалында жүретін, үздіксіз сигналдың есептемелерін осындай кодалау әдістерінің біреуі пайдаланылады. Бұл жағдайда бірнеше кезекті импульстар уақыт өсі бойынша қосындылық, бір өте енді импульске ұласып кетуі мүмкін.

Ескеретін нәрсе, кванттау оперциясы процесінде әрбір есептеме үзіліссіз сигналдың бекітілген мәндерінің біреуімен әрқашанда дәл бірдей болуы мүмкін емес. Сондықтан оны ең жақын берілген деңгейге дейін дөңгелектейді. Осының нәтижесінде дискреттіктен аналогтық сигналды қайта қалпына келтіргенде, бастапқы сигналдан алынған сигналдың ауытқу дәрежесін сипаттайтын жүйелік қателіктер туындайды. Осы кванттау қателіктері дискреттік және цифрлық сигналдар теориясында маңызды рөл атқарады.

Дискреттелген сигналдан бастапқы үздіксіз сигналды кішкене бұрмаланулармен (қателіктермен) қайта қалпына келтіру үшін, дискреттеу адымын рационалды таңдау керек. Сондықтан, аналогтық сигналды дискреттікке түрлендіргенде міндетті түрде дискреттеу адымы Δt шамасы туралы мәселе туындайды. Келесі көңілге қонымды идеяны түсіну қиын емес. Егер аналогтық сигналдың әлдебір жоғарғы жиілік F_в-пен шектелген төменгі жиілікті спектрі бар болса (яғни u(t) функциясының , амплитудасының шұғыл өзгерісі жоқ, жәйлап өзгеретін қисығы болса), онда кішкентай уақыттық дискреттеу Δt интервалында осы функция амплитуда бойынша айтарлықтай өзгеруі мүмкін емес.

Аналогтық сигналды оның есептемелерінің тізбегі бойынша қайта қалпына келтіру дәлдігі дискреттеу интервалы Δt шамасына тәуелді екені айдан анық. Қаншама ол кішкене болған сайын u(t) функциясы есептемелер нүктесінен өтетін бірқалыпты қисықтан соншама аз айырмашылығы болады. Бірақ дискреттеу интервалы Δt кішірейген сайын ақпаратты өңдейтін аппаратура күрделілігі мен көлемі ұлғая түседі. Жеткілікті үлкен Δt дискреттеу интервалында бұрмалану ықтималдығы арта түседі немесе аналогтық сигналды қайта қалпына келтіргенде ақпаратты жоғалтып алуымыз мүмкін.

Дискреттеу интервалының оптималды шамасы Котельников теоремасымен (басқа атаулары – есептемелер теоремасы, Шеннон теоремасы, Х.Найквист теоремасы) анықталады. В.А.Котельников теоремасының маңызды теориялық және іс жүзіндегі маңызы бар: аналогтық сигналды дұрыс дискреттеуге мүмкіндік береді және осы сигналды қабылдағыш аяғында есептемелер мәндері бойынша қайта қалпына келтірудің оптималды әдісін анықтайды.

Котельников теоремасының ең белгілі және қарапайым түсіндірмелерінің біріне сәйкес, спектрі әлдебір F_в жиілікпен шектелген кезкелген (произвольный)? сигнал u(t), t = 1/2 F_в уақыт интервалымен жүретін есептемелер мәндерімен толық қайта қалпына келтірілуі мүмкін.

В.В.Котельниковтың тұжырымдамасында ( 1933 ж.) мынандай сөздер бар: «үздіксіз сигналдарды қандай да болмасын дәлдікпен бірінен кейін бірі 0,5/F_в секундтен соң жүретін сандар көмегімен таратуға болады», яғни негізінде алғашқы рет сигналдарды таратудың цифрлық тәсілі туралы мәселе қойылған.

Дискреттеу интервалы Δt мен F_в жиілікті радиотехникада кейде сәйкесті түрде Котельников интервалы және Найквист жиілігі деп атайды. Аналитикалық түрде Котельников теоремасы қатармен көрсетіледі:

(2.29)

Мұнда k – есептеме нөмірі; u(kt)— есептеме нүктелеріндегі үздіксіз сигналдың мәні ; - сигналдың спектрі орташа жиілігі.

Котельников теоремасын дәлелдеу үшін S() спектральдық тығыздығы

жиілік жолағында орналасқан кезкелген үздіксіз сигналды қарайық ( 2.10 –суреттегі үзілісті сызық).

2.10- сурет. Периодты функцияның спектралдық тығыздығын бейнелеу

Ойша S() спектралдық тығыздықтың графигін периодты қайталанатын мәндеріне симметриялы түрде қосымшалайық (2.10 –суреттегі үзікті сызықтар).

Осылайша алынған периодты функцияны аргументі t- ны - ға , жиілігін 1 = B - ды t –ға және формалды n -ды k -ға ауыстырып; Фурье қатарына жіктейміз.

Сонда

(2.30)

Период — екенін, ал дискреттеу интервал ескеріп, жазамыз

(2.31)

Фурье кері түрлендіруін пайдаланып, бастапқы үзіліссіз сигналды келесі түрде көрсетеміз:

(2.32)

Осылайша уақыттың әлдебір k – есептемесі үшін дискреттелген сигналдың мәнін жазамыз. Уақыт болғандықтан , онда

Осыны (3.5) өрнекпен салыстырып, екенін көреміз. Осы қатынасты ескерсек, спектралдық функция (3.4) бірнеше қиын емес түрлендірулерден кейін, келесі қалыпқа келеді:

(2.33)

Енді былай жасайық: (2.33) өрнегін (2.32) қатынасына апарып қоямыз, интегралдау және қосындылау ретін өзгертейік, деп алып, интегралды есептейміз. Нәтижесінде мынандай өрнекті аламыз:

(2.34)

Осы қатынастан көрініп тұр, үздіксіз функция шынында да уақыттың есептемелік сәттеріндегі оның амплитудасының дискреттік мәндерінің жиынтығымен анықталатыны, ал бұл Котельников теоремасын дәлелдейді.

уақыт аралығында бір-біріне ортогональ

(2.35)

түріндегі сигналдар, есептемелер функциялары, базистік функциялар немесе Котельников функциялары деп аталады. Котельников базистік функциясының графигі 2.11 – суретте берілген. Базистік функциялардың әрбіреуі өзіне ұқсас жақын функцияға немесе қарағанда дискреттеу интервалы -ға жылжыған. (2.35) формуланың және графиктің талдауынан көрініп тұр, сигналы, тік бұрышты импульстің төмендейтін спектралдық тығыздығының ол да сипаттайтын сигналымен де бейнеленеді.

2.11 – сурет. Котельников базистік функциясы графигі

Берілген u(t) үздіксіз сигналды Котельников қатарымен (дәлірек айтқанда, аппроксимациялау) бейнелеу 2.12 – суреттегі диаграммалармен көрсетілген.

Радиотехникада сигналдар теориясы мен техникасында Котельников теоремасы (есептемелер теоремасы) негізінен қолданылады: егер s (t) функциясы спектрінде ең жоғары жиілік f_m -нен кіші болса, онда s (t) функциясы бір-бірінен секундтан аспайтын уақыт сәттеріндегі өзінің мәндерінің тізбегімен толық анықталады.

Яғни Котельников теоремасы бірдей уақыт аралықтарында алынған есептемелік мәндерін (іріктеулерін) ескере отырып шектелген спектрі бар сигналдың лездік мәндерін өте дәл қайта қалпына келтіру мүмкіндігін қарастырады.

Cонымен осы теоремаға сәйкес спектрі бойынша ең жоғары жиілікпенен _{m =} 2 f_m шектелген s(t) сигналын катар түрінде көрсетуге болады:

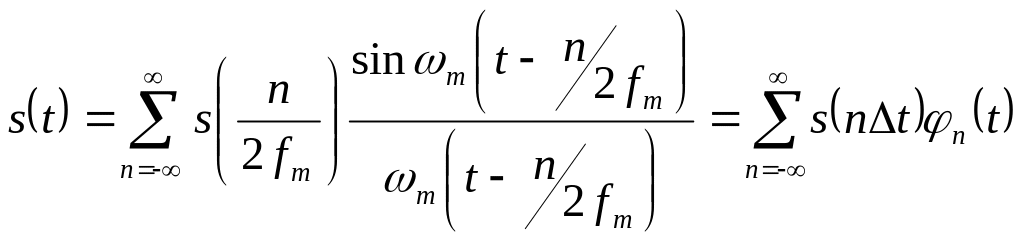. (2.36)

Осы өрнекте мәні уақыт осіндегі екі есептемелік нүкте арасындағы интервалды анықтайды, ал - t = nt уақыт сәттеріндегі s(t) функциясының іріктеулері.

Осы (2.36) қатарда тұрған

функциясының мынандай қасиеттері бар:

а) t = nt нүктесінде _n (nt ) = 1, ал t =k t нүктелерінде _n(kt ) = 0, мұнда k -кезкелген бүтін оң сан, немесе n -нен бөлек теріс сан;

ә) _n (t) функциясының спектралдық тығыздығы    _m жиіліктер жолағында бірқалыпты және .

_n (t) функциясының ₀ (t) -дан уақыт осі бойынша nt -ға жылжу айырмашылығы болатындықтан, _n (t) функциясы спектралдық тығыздығы

 -_n _m және

Ф = 

 0 ,  - _m және _m болғанда.

2.12 – сурет. Котельников қатарымен үздіксіз сигналды аппроксимациялау

Котельников қатарымен берілген бейнеленген сигналды аппаратуралық түрде синтездеуге болады. Котельников теоремасының маңызды ерекшелігі оның конструктивтік сипатында: ол сигналды сәйкесті қатарға жіктеу мүмкіндігін көрсетумен бірге, өзінің берілген есептік мәндері бойынша үздіксіз сигналды қайта қалпына келтіру әдісін де анықтайды (2.13 – сурет).

Шығыс қысқыштарында есептік функцияларды Sс_k(t;₀) шығаратын генераторлар жиынтығы бар дейік. Генераторлар басқарыла алады – олардың сигналдарының амплитудалары s_k есептік мәндеріне пропорционал. Егер шығыстарындағы тербелістерді біріктіріп, оларды сумматорға берсек, онда сумматордың шығысында (2.35) формуласына сәйкес s(t) синтезделетін сигналдың ілездік мәндерін алуға болады.

s_-1 s₀ s₁

. .... .....

Sc_-1 Sc₀ Sc₁

+

2.13-сурет. Котельников қатары бойынша сигнал синтезін аппаратуралық түрде

іске асыру

Мысал 2.1. Тік бұрышты, амплитудасы А, аралығында анықталған

импульс үшін (2.14-сурет) функциялар жүйесі

бойынша жалпыланған Фурье қатарын жазып беріңдер. Импульс ұзақтылығы

_и =Т/2. S(t) функциясын Фурье қатарының екі, үш және төрт қосындыларымен аппроксимация жасағанда салыстырмалы орташаквадратикалық қатені анықтаңдар.

Функциялардың нормалары квадраттарын табайық.

s(t) ₀² _n² = T/2.

A

Жалпыланған Фурье қатары коэффициенттерін

анықтайық

t

-T/4 0 T/4

2.14-сурет. Тік бұрышты импульс

= .

Сонымен берілген функциялар жүйесі бойынша жалпыланған Фурье қатары

.

Салыстырмалы орташа квадратикалық қателік келесі өрнекпен анықталады

.

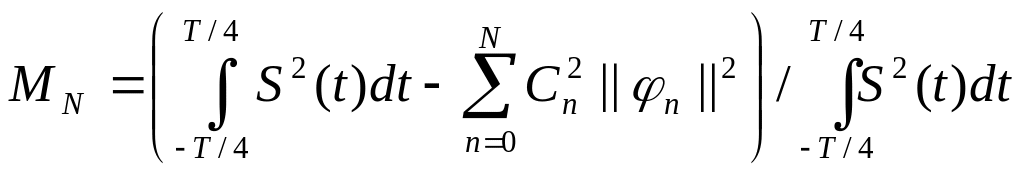Табылған C_n және ||_n||² мәндерін қойып, аламыз

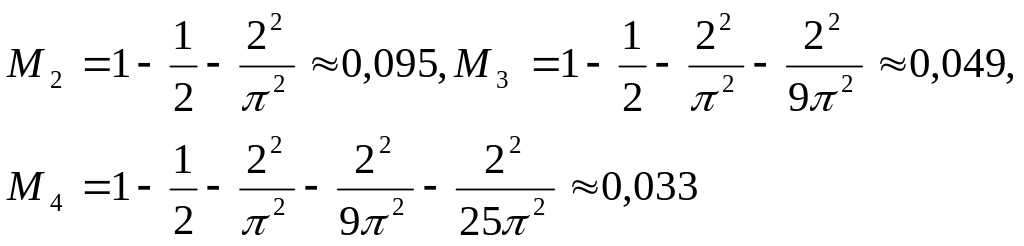
Мысал 2.2. s(t) = cos (₀t + ₀) сигналы берілген.

Есептемелер t₀ арасында әлдебір бекітілген интервалды таңдап алып, спектрі шектік жиілік _ж = /t₀ - дан жоғары жиіліктерде құрастырушылары болмайтын кезкелген сигналды есептемелері бойынша бірмәнді түрде қайта қалпына келтіру мүмкіндігін аламыз.

Егер ₀  _ж болса, онда қарастырылып отырған гармоникалық сигналға (2.15-сурет) Котельников теоремасын қолдануға болады; осы сигналдың есептемелік мәндері (таңдаулықтары)

s_k = cos (k₀/_ж  ₀).

Солдан ₀ –жиілігі _ж –ға ұмтылатын шектік жағдайда, яғни

- да,

гармоникалық сигналдың әрбір периодына дәл екі таңдаулық келуі тиіс. Сөйтіп сигналды бірмәнді қайта қалпына келтіруге болады (2.15 – сурет).

2.15 – сурет. Сигналды бірмәнді қайта қалпына келтіру

мүмкін болатын жағдай

Егер Котельников теоремасы шарттары бұзылса және уақыт бойынша есептемелер жеткілікті жиі аралықта алынбаса, онда бастапқы сигналды нақты түрде қайта қалпына келтіру мүмкін емес.

Бақылау сұрақтары

1. Қандай белгілері бойынша радиотехникалық сигналдарды жіктейді?

2. Қандай сигналдар аналогтыққа, дискреттікке және цифрлікке жатады?

3. Детерминацияланған және кездейсоқ сигналдардың қандай айырмашы-лықтары бар?

4. Қандай сигналдар кванталған деп аталады?

5. Шуылдар мен бөгеуліктер деген қандай сигналдар?

6. Сигналдың спектрі дегеніміз не?

7. Қандай мақсатпен сигналдарды спектралдық бейнелеумен береді?

8. Сигналдарды неге динамикалық түрде көрсетеді?

9. Дельта-функция дегеніміз не?

10. Қосылу функциясы қайда қолданылады?

11. Қандай сигналдар шектелген деп аталады?

12. Котельников теоремасы анықтамасын айтып бер.

13. мәні нені көрсетеді?

14. Бастапқы үзіліссіз сигналды дискреттіктен қалай қайта қалпына келтіруге болады?

15. _n (t) функциясының қандай қасиеттері бар?

16. Дискреттеу адымы шамасы қалай тандап алынады?

17. Дискреттеу деген қандай процес?

ІІІ- тарау