2.4 Периодты емес сигналдардың

спектралдық бейнеленуі.

Периодты емес (импульстік) сигналдарды спектралдық бейнелеу теориясында жасанды әдіс пайдаланады, осындай сигналдарды шексіз үлкен жүру интервалы (периодты)   бар периодты сигналдармен формалды алмастыру арқылы.

Әлдебір берілген функция u(t) шекті ұзақтылығы бар дара импульстік сигналды аналитикалық түрде сипаттайды дейік (2.10, а – сурет). Ойша оны осындай әлдебір Т интервалмен жүретін импульстық сигналдармен толықтырып , (2.9, ә - сурет) сондай импульстардың периодты тізбегін u(t) = u(t + nT ) аламыз.

2.9 –сурет. Периодты емес сигналдар:

а –дара импульс; ә - шартты периодтық бейнелеу

Жасанды енгізілген 0, Т интервалы сыртында бастапқы сигнал нөлге тең болуы үшін, импульстар қайталау периодын шексіз ұлғайту керек. Шегінде периодты ұлғайтқанда, және   барлық импульстар оңға және солға шексіздікке кетеді де, u(t) переиодты тізбегі қайтадан дара импульске u(t) айналады. Бұл жағдайда (2.10) және (2.11) өрнектері орын алады. (2.11) формуласын (2.10) -ға қойып , периодты функцияны жазамыз:

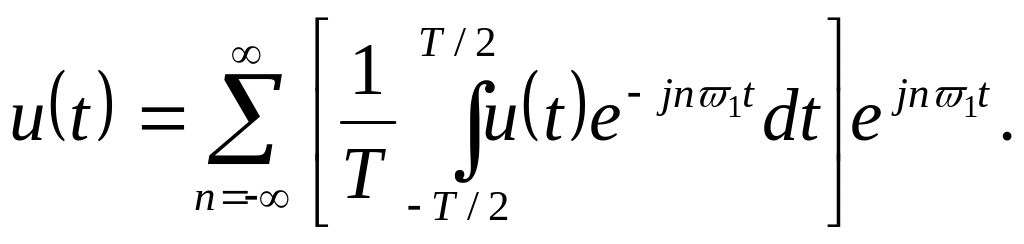
Жүру периоды Т = 2/₁ болғандықтан

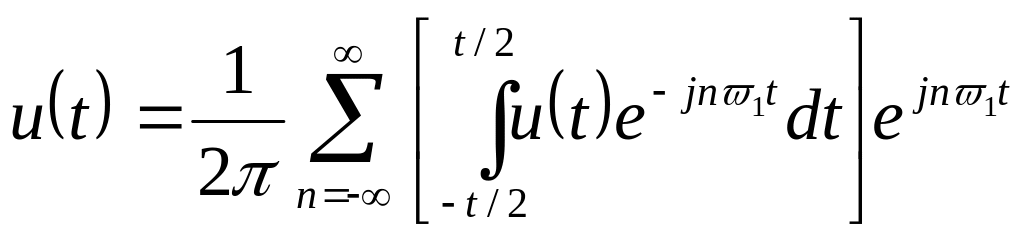(2.21)

Импульстер жүру периоды Т ұлғайғанда тіке сызықтылықты спектр тұтаса бастайды. Шекті жағдайда, яғни Т , спектралдық сызықтар арасында бірдей қашықтықтар соншама кішірейіп, спектр тұтасып кетеді, ал жеке спектралдық құрастырушылар амплитудалары шексіз кішкентай болады. Бұл жағдайда импульстер жүру жиілігі ₁= 2  0 -да d –ге айналады, ал дискретті айнымалы n₁ – ілездік (ағымдық) жиілікке , ал қосынды интегралға айналады. u_n (t) импульстардың периодты тізбегі u(t) дара импульс болып, (2.21) өрнек былай жазылады:

(2.22)

мұнда жақша ішіндегі интеграл жиіліктің комплексті функциясы. Оны былай белгілеп

(2.23)

табамыз

(2.24)

(2.21) және (2.22) өрнектері сигналдар теориясында фундаменталды орын алады да, сәйкесті түрде Фурьенің тіке және кері түрлендірулері деп аталады. Олар өзара нақты уақыт функциясын (сигналды) u(t) және жиіліктің комплекстік функциясын S() байланыстырады. Сонымен, Фурье интегралы (2.21) сигналдың шексіз кішкене амплитудалары бар үздіксіз (тұтас) спектралдық құрастырушылар тізбегінен тұрады. S() функциясын спектралдық тығыздық деп атайды. Ол периодты емес сигналдың гармоникалары амплитудаларының жиіліктер  өсі бойымен тұтастай таралу қарқындылығын сипаттайды. Осы жәйт периодты емес сигналдың спектралдық тығыздығының, әрбір гармоникалық құрастырушысының нақты белгілі жиілігі бар және көрші жиілігінен ₁ =2/T – шамасына әрі орналасқан периодты сигналдың дискретті спектрінен негізгі айырмашылығы болып табылады.

Периодтық сигналдың дискреттік спектрі мен периодты емес сигналдың спектралдық тығыздықтары өлшемдері әртүрлі. Дискреттік спектрдің амплитуда өлшем бірлігі В немесе А. Ал спектралдық тығыздық өлшем бірлігі В/Г_Ц немесе А/Г_Ц.

Периодты емес сигнал u(t) және оның спектралдық тығыздығы S () Фурье түрлендіруі қосағымен бір мәнді өзара байланыста болғандықтан, Фурье түрлендіруі берілген сигнал пішіні бойынша спектралдық тығыздықты және керісінше спектралдық тығыздық бойынша оның пішінін табуға мүмкіндік береді.

Фурье түрлендіруінің негізгі қасиеттері.

Қолданбалы мақсаттар үшін сигналдың әртүрлі түрлендірулері мен осы түрлендірулерге сәйкесті оның спектралдық тығыздығы өзгерістері арасындағы байланыс маңызды. Осындай негізгі радиотехникалық түрлендірулерді қарастырайық.

Сигналдың уақыт бойынша жылжуы (кешігу теоремасы)

S₁() спектралдық тығыздығы бар u₁(t) сигналы t_с әлдебір уақытқа кідіртілді дейік. Бұл жағдайда u₂(t) = u₁(t –t_c ), және де кешіктірілген сигналдың спектралдық тығыздығы тіке Фурье түрлендіруіне (2.17) сәйкес мынадай түрге келеді:

.

Интегралдың жаңа айнымалысы - ны енгізіп, табамыз

(2.25)

Сөйтіп, сигналдың уақыт бойынша әлдебір t_c интервалға жылжуы тек қана спектралдық тығыздықтың аргументінің t_c шамаға өзгеруіне әкеледі, ал оның модулы өзгеріссіз қалады. Іс жүзінде уақыт бойынша сигнал жылжуы әртүрлі тасымалдаушыларға аудио – және видеожазуда іске асырылады. Қаншама ұзақ (теориялық жағынан) жазба сақталса да, сигнал спектрі (және пішіні) ешқандай өзгеріссіз қалады.

Сигнал спектрін жылжыту(жылжыту теоремасы). Осы теореманың мәні мынада: егер S₁() – u₁(t) сигналының спектралдық тығыздығы болса, онда бастапқы спектрді жиіліктер өсі бойынша  шамасына жылжыту арқылы алынған

S₂(+) спектралдық тығыздығы -сигналына сәйкес келеді. Шындығында:

(2.26)

Мұндай сигналды түрлендіруді байланыс жүйелерінде немесе сигнал спектрін бір жиіліктер жолағынан екіншісіне тасымалдағанда, немесе модуляцияда қолданады. (2.26) қатынасынан көрініп тұр, осындай түрлендірулер нәтижесінде сигнал спектрі жылжыту жиілігіне тең  шамасына ығысады.