2.3. Периодты сигналдың спектральдық көрсетілуі

Көп жағдайда құрылымы бойынша күрделі емес детерминдалған сигналдарды математикалық түрде бейнелеуде қиындықтар туындайды. Сондықтан радиоэлектроника мен байланыс техникасында өте ыңғайлы әдісті қолданады, мұнда құрылымы және қалпы бойынша күрделі сигналдарды элементар функциялармен сипатталатын идеалданған математикалық моделдер жиынтығымен бейнелейді (жуықтап көрсетеді).

Зерттелетін сигналды сипаттаудың ең қолайлы әдісі оны базистік деп алатын әлдебір өзара байланысқан уақыттың элементарлық жүйесі көмегімен аналитикалық түрде көрсету:

 _o(t) , ₁(t) , ₂ (t) , … _i _i (t) …. , (2.7)

мұндағы i = 1 ,2 , 3 , ....

u(t)-сигналды элементар моделдермен көрсету әлдеқайда қарапайымдалады , егер ортонормаланған қасиеті (ортогоналдық және нормаланғандық) бар базистік функциялар V_i (t) жүйесі таңдап алынса. Математикада базистік функциялардың осындай жүйесін ортонормаланған базис деп атайды.

u(t) және (t) екі функциясы t₁ , t₂ уақыт аралығында ортогоналды , егер олардың скалярлық көбейтіндісі (көбейтінді интеграл)

^t ₂

 u(t)  (t) dt   ( 2.8)

t₁

осы функциялардың ешқайсысы да нөлге тепе-тең болмаған жағдайда .

Функциялардың (сигналдардың) ортогоналдығы қасиеті олардың анықталу аралығымен міндетті түрде байланысты (2.6 – сурет)

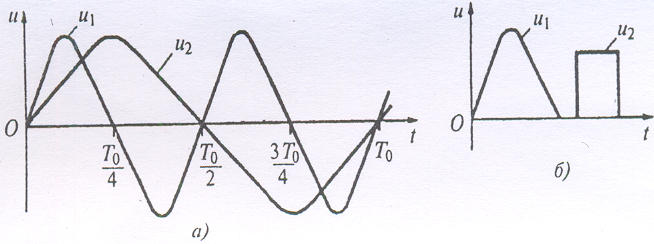
2.6 – сурет. Сигналдар ортогоналдығы:

а –аралықта; б - әртүрлі уақытта пайда болуынан

Мысалы , u₁(t)  sin (2 t /T_o ) мен u₂(t)  sin (2t /T_o ) гармоникалық сигналдары , ұзақтылығы T_o жартылай периодтардың бүтін санына тең кезкелген уақыт интервалында ортогоналды. (2.6,а –сурет).

Сондықтан, бірінші периодта u₁(t) мен u₂(t) сигналдары 0 ... Т₁ /2 интервалында ортогоналды емес. 2.6, б - суретте сигналдар ортогоналды, олардың туындау түрінен.

Математикадан белгілі, егер ортогоналды жүйедегі (2.1) кезкелген қос функция үшін

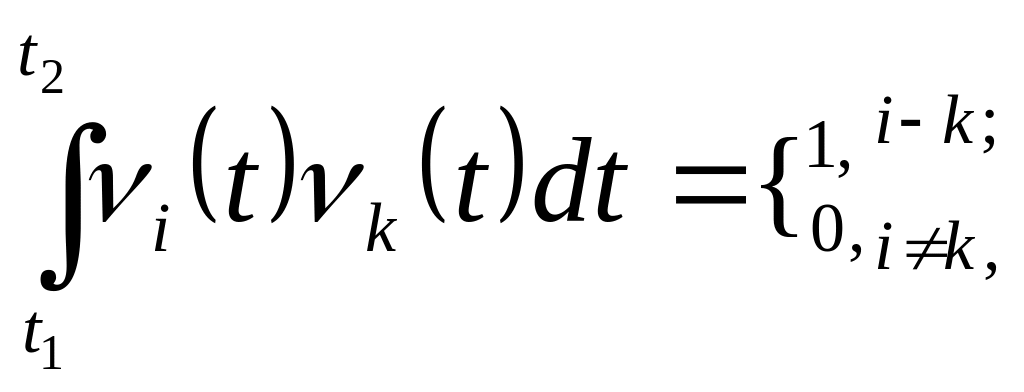(2.9)

шарты орындалса, онда осы функциялар жүйесі ортонормаланған (1 –ге нормаланған).

Белгілі француз математигі Ж. Фурье әлдебір функцияның уақыт бойынша кезкелген өзгерісін әртүрлі амплитудалары , жиіліктері және бастапқы фазалары бар гармоникалық тербелістердің шекті немесе шексіз қатары қосындысы түрінде бейнелеуге болатынын көрсеткен. t₁, t ₂ уақыт аралығында еркін (произвольный) үздіксіз сигнал u(t) әрекет етеді дейік және оны жуықтап көрсету үшін, ортоноαрмаланған идеалды функциялар жүйесі (2.7) пайдаланылсын. Сонда берілген сигнал Фурьенің жалпылаған қатарымен көрсетілуі мүмкін

, (2.10)

мұнда с_i - әлдебір тұрақты коэффициенттер.

Осы қатардың коэффициенттерін анықтау үшін базистік функциялардың біреуін к ерікті нөмерімен _k(t ) таңдап алайық. (2.8) өрнегінің екі жағын да осы функцияға көбейтіп , нәтижесінен уақыт бойынша интеграл алайық

Таңдап алынған функциялардың базисы ортонормаланғандықтан осы теңдіктің оң жағындағы қосынды мүшелері t  k болғанда нөлге тең болады, қосындының тек нөмері i  k мүшесі ғана нөлге тең болмайды, сондықтан

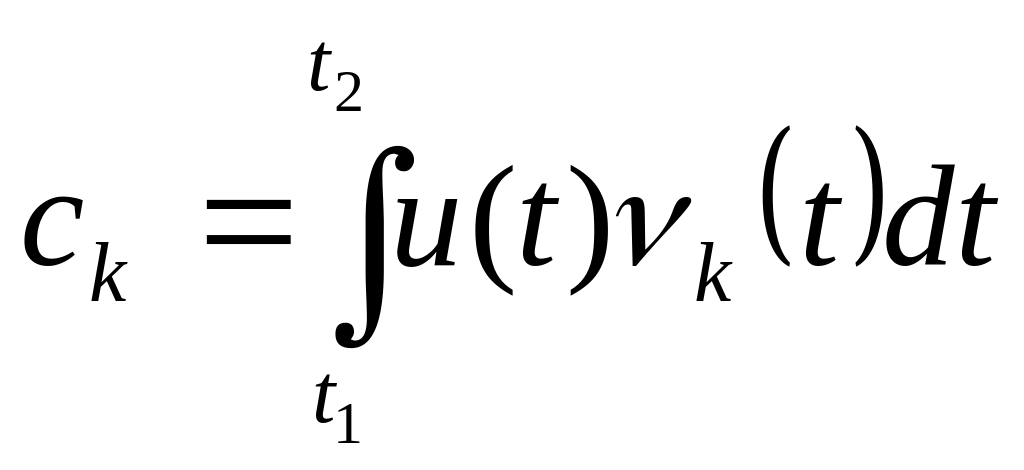(2.11)

с_к коэффициенттер жиынтығы талданатын u(t) сигналды толығымен анықтайды да, оның спектрі деп аталады. Басқаша айтқанда, сигналдың жеке гармоникалық құастырушылары (компоненттері) оның спектрін құрады.

Радиотехникада және байланыс теориясында тригонометриялық (синусоидалдық және косинусоидалдық) функциялардың ортонормаланған базистері кеңінен қолданыс тапты. Бұл мына жағдайға байланысты: гармоникалық тербелістерді өте жеңіл қоздыруға (генерация жасауға) болады; гармоникалық тербеліс тұрақты көрсеткіштері бар кезкелген сызықты тізбек арқылы өткенде теориялық жағынан толығынан өзінің пішінін (формасын) сақтап қалады, оның тек амплитудасы мен бастапқы фазасы өзгереді. Үздіксіз детерминалданған сигналдарды әртүрлі еселі жиіліктері бар гармоникалық тербелістердің тұрақты құрастырушысы мен қосындысы жиынтығы түрінде көрсету амалын спектралдық жіктелуі (бейнеленуі) немесе гармоникалық талданылуы деп атайды.

Детерминалданған сигналдардың қарапайым түрі – периодтық сигналдың спектралдық жіктелуін қарайық. Периодтық деп ретті уақыт аралықтары арқылы қайталанатын (2.7-сурет) және

u(t) = u(t + nT ),

мұнда Т – импульстардың қайталану немесе жүруі периоды, n – 0,1,2,... ; шартын қанағаттандыратын кезкелген сигналды (функцияны) айтады.

u

E

-T -T/2 0 T/2 T/2 _и t

2.7 – сурет. Периодты сигнал

Жалпы түрде импульстердің периодты тізбегі

u(t) = (2.12)

өрнегімен сипатталады.

Мұнда u₀ (t) жеке импульс пішіні , ол келесі көрсеткіштермен сипатталады: амплитудасы (биіктігі) h=Е; ұзақтылығы (ені) _u ; жүру периоды Т=1/Ғ ( Ғ – жүру жиілігі); тактылық нүктелерге қарағандағы импульстер орнымен. Периодтық сигналдарды спектралдық түрде көрсеткенде гармоникалық функциялардың ортонормалды базисы өте ыңғайлы:

(2.13)

мұнда ₁= - импульстердің жүру жиілігі.

(2.8) бойынша интегралдарды есептеп, -Т/2, Т/2 аралығында берілген функциялардың ортонормаланған екеніне жеңіл көз жеткізуге болады. Осы функциялардың кезкелгені периодтылық шартын (2.12) қанағаттандырады , өйткені олардың жиеліктері еселі.

Перодтық сигналды ең көп тараған Фурье қатарының тригонометриялық пішінімен (формасымен) көрсетейік:

u(t) = (2.14)

Осы қатынаста сигналдың келесі компоненттері бар:

- тұрақты құрастырушысы:

(2.15)

-косинусоидал құрастырушылардың амплитудалары:

(2.16)

-синусоидал құрастырушылардың амплитудалары:

(2.17)

Жиілігі ₁ спектралдық құрастырушыны радиотехникада бірінші (негізгі) гармоника деп, ал жиліктері n₁ (n1) құрастырушыларды – периодтық сигналдың жоғары гармоникалары деп атайды.

Математика курсынан белгілі, егер сигнал жұп уақыт функциясы u(t) = u(-t) болса, онда Фурье қатарының тригонометриялық жазбасында (2.14) синусоидалық коэффициенттер b_n болмайды, өйткені (2.16) өрнекке сәйкес олар нөлге тең болады. Уақыттың тақ функциясымен анықталатын u(t) сигналы үшін, керісінше косинусоидалық коэффициенттер α_n– нөлге тең де, қатар тек b_n құрастырушылардан тұрады.

Математикалық жағынан, берілген сигналды сипаттайтын (2.14) өрнегін , басқа Фурье қатарына эквивлент пішінде берген қолайлы:

(2.18)

мұнда - амплитуда, ал _n =arctg(b_n/α_n) - сигналдың n – гармоникасы бастапқы фазасы.

Радиоэлектроникада және байланыс теориясында Фурьенің комплексті қатары пайдаланылады

(2.19)

мұнда

(2.20)

-n – ші гармоника комплексті амплитудасы.

(2.18) қатынасынан периодты сигналды Фурье қатары комплексті пішінмен спектралдық бейнелеуі оң және де теріс жиіліктерден тұратынын анықтауға болады. Бірақ табиғатта теріс жиілік болмайды, бұл математикалық абстракциядан туындаған түсінік.

Радиотехникалық сигнал спектрі туралы көрнекті түрде оның графикалық бейнесі – спектралдық диаграмма бойынша айтуға болады. Сигналдар теориясында амплитудалы – жиіліктік және фазалы - жиіліктік спектрлер деп бөледі. Гармоникалық құрастырушылар амплитудалар жиынтығы A_n амплитудалар спектрі деген атаумен белгілі, _n - фазалар спектрі , C_n - комплекстік спектр деп аталады (2.8 – сурет)

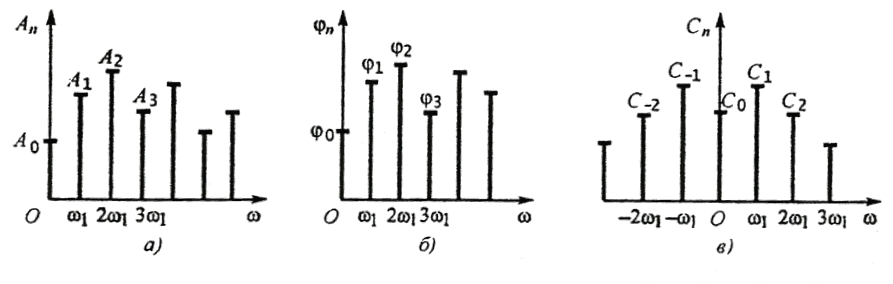
2.8 – сурет. Периодтық сигнал спектрлері:

а) – амплитудалық; ә) – фазалық ; б) – комплекстік

Спектралдық диаграммаларда абцисса өсі бойымен ағымдық жиілікті , ал ордината өсы бойымен - нақты немесе комплексті талданатын сигналдың гармоникалық құрастырушыларының амплитудасын немесе фазасын салады.

Периодтық сигналдың спектрін тіке сызықтылықты немесе дискретті деп атау қабылданған, өйткені ол биіктігі A_n амплитудаға тең сәйкесті гармоникалардың жеке сызықтарынан тұрады. Барлық спектрлер түрінің ішінде ең ақпаратқа байы амплитудалық, өйткені оның көмегімен талданатын сигналдың жиіліктік құрамында сол және басқа гармоникалардың сандық болмысын бағалауға болады.