3.2. Жиілікті және фазалы модуляцияланған сигналдар және

олардың спектрі

Басқарушы сигналдарды амплитудасы өзгермейтін жоғары жиілікті тасымалдаушы сигналдың жиілігі немесе фазасы өзгерістері арқылы түрлендіруге болады. Мұндай модуляция бұрыштық деп аталады өйткені негізінде басқарушы сигналдың заңы бойынша өте жоғары жиілікті тербелістің фазалық бұрышы (t) өзгеруі іске асырылады.

Бұрыштық модуляциясы бар тербелістер келесі өрнекпен беріледі;

u(t) = U_тsin  (t), (3.14)

мұнда (t) =_тt + (t) - уақыт бойынша өзгеретін фазалық бұрыштың ілездік мәні.

Басқарушы сигналдың функциясы ретінде _т(t) , немесе  (t) алынуына қарай сәйкесті түрде бұрыштық модуляция жиіліктік (ЖМ) немесе фазалық (ФМ) деп аталады.

Жиіліктік модуляция. Жиіліктік модуляцияда

 t = _т + ke(t),

мұнда k –пропорционалдық коэффициенті , е(t) – модуляциялайтын сигнал амплитудасы.

Фазалық жиілік (t) фазалық бұрыштың уақыт бойынша өзгеру жылдамдығы болғандықтан , яғни

_т (t)=d (t)/dt, онда

t

(t)=   (t)dt+₀ ,

0

Мұнда ₀ –бастапқы фаза . Осы өрнекті (3.14)-ға қойып, табамыз

t

u(t) = U_m sin   _т (t) dt + ₀  . (3.15)

0

Бұл жиілікті модуляцияланған сигналдың жалпы өрнегі.

Бір тоналды модуляцияны қарайық

е(t)=E cos t

сонда тасымалдаушы сигналдың ілездік жиілігі мына түрде беріледі

 t = _т + ke(t) _т +k E cos t  _т + _т cos t (3.16)

мұнда _т =kE –модуляциялайтын кернеу амплитудасына пропорционал

жиіліктің максималды аутқуы, девиация деп аталады.

Бұл жағдайда (3.15) бойынша аламыз

t

u(t) = U_msin [ (_т + _т cos t) dt + ₀] = U_msin(_тt +_т/  sint +₀) =

0

= U_msin(_тt + msint +₀), (3.17)

мұнда m = _т/ = kE/ модуляция индексі, ол фазаның максималды өзгерісін көрсетеді, яғни m =_max.

Сөйтіп, жиіліктік модуляцияда (ЖМ) жиілік девиациясы модуляциялайтын кернеу амплитудасына пропорционал да, модуляция жиілігіне тәуелді емес; фазаның максималды өзгерісін сипаттайтын модуляция индексі амплитудаға тіке пропорционал да модуляциялайтын кернеу жиілігіне кері пропорционал. Және де жиіліктік модуляцияда модуляция индексі модуляциялайтын жиілікке кері пропорционал да, ал жиілік девиациясы  - жиілігіне тәуелді емес. Сондықтан жиілік өскен сайын модуляция индексі кішірейеді, бұл жиілікті - модуляцияланған сигналдың спектрінде оның тұрақты енінде гармоникалық құрастырушылардың санының азаюына әкеледі, яғни көрші бүйірлік гармоникалар арасындағы аралықтар (интервалдар) ұлғаяды.

Жиіліктік біртоналды модуляциядағы тербелістер түрі 3.7 –суретте көрсетілген.

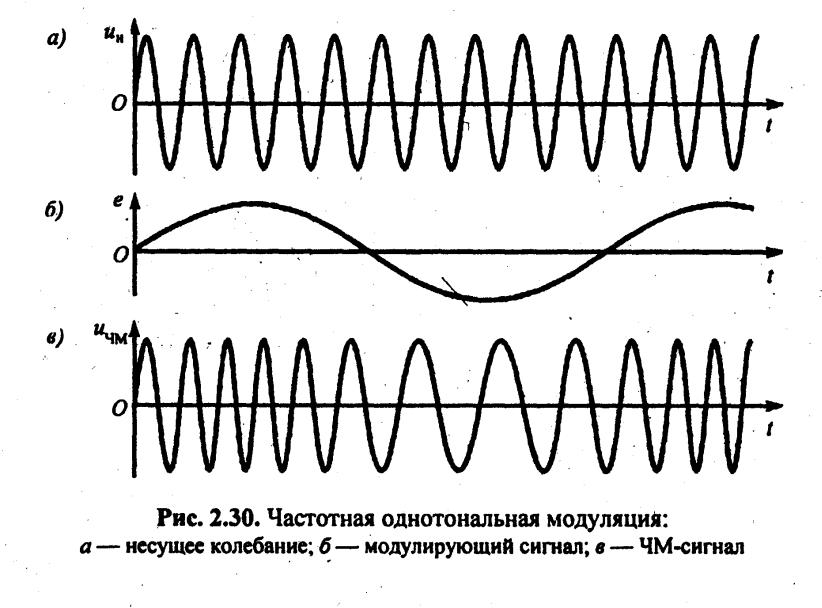
3.7 –сурет. Жиіліктік бір тоналды модуляция: а – тасымалдаушы тербеліс;

б-модуляциялайтын сигнал; в – ЖМ -сигнал

Фазалық модуляция.

Фазалық модуляцияда  модуляциялайтын сигнал амплитудасы функциясы болып табылады , яғни

t = ₀ + ket

Фазалы модуляцияланған сигнал жалпы жағдайда келесі өрнекпен сипатталады

u(t) = U_т sin [_т t + t] . (3.18)

Бір тоналды модуляцияда

t = ₀ + kE sint = ₀ + _max sint.

(3.18) –ге t мәнін қойғаннан кейін табамыз:

u(t) = U_m sin (_т t + ₀ + _max sint), ( 3.19)

мұнда _max - модуляциялайтын кернеу амплитудасына пропорционал фазаның максималды өзгерісі. _max –ді басқаша бұрыштық модуляция индексі деп атайды да, m_б – деп белгілейді. Сонымен фазалық модуляцияда

m_б = _max = kE ( 3.20)

уақыт бойынша өзгеретін (t) фазалық бұрыштың ілездік мәні тең болады:

(t) = _т t + ₀ + m  sint, (3.21)

Осыдан

 = d(t)/dt = _т + m sint,

мұнда m  = _max = _т = kE модуляциялайтын тербелістің амплитудасы мен жиілігіне тура пропорционал фазалық модуляциядағы _т- дан жиіліктің максималды ауытқуы.

Сөйтіп фазалық модуляцияда фазаның максималды өзгерісін сипаттайтын модуляция индексі модуляциялайтын кернеу амплитудасына пропорционал да, модуляция жиілігіне тәуелсіз болады; жиілік девиациясы және модуляциялайтын кернеу амплитудасына және жиілігіне тіке пропорционал өзгереді. Жиіліктік және фазалық модуляцияны қарастырғаннан көрініп тұр: жиіліктік модуляцияны жүргізгенде бір уақытта фазалық модуляцияны алады, сосын керісінше, сөйтіп олар бұрыштық модуляция түрлері болып табылады.

Бұрыштық модуляциядағы жиіліктер спектрі

Модуляцияның жоғары индекстерінде ( m1) бұрыштық модуляцияда модуляцияланған сигнал спектрі үшін былай жазамыз:

u (t) = U_тJ₀(m) sin _тt + U_т

+U_т ,

Мұнда J_n(m) - гамма функция. Осыдан көрініп тұр, бір тоналды бұрыштық модуляцияда сигнал спектрі , бүйірлік жиіліктердің жоғарғы және төменгі жасақтарын құратын көптеген гармоникалардан тұрады, жолақта олардың саны m индексі өскен сайын көбейе түседі, ал осы жиіліктердің амплитудасы берілген модуляция индексінде J_n(m)- пропорционал. n_max m+ 1 ден бастап J_n(m)- Бессель функциясының осыған сәйкес гармония амплитудаларының мәндері өте кішкентай болатындықтан қатарда оларды ескермей-ақ қоюға болады.

Сонда бұрыштық модуляцияда спектр ені

 = 2n_max = 2 (m + 1) (3.22)

жиіліктік модуляция жағдайында, мысалы m = _T/ болғандықтан

табамыз:   (   ) болғандықтан m1 өте үлкен мәндерінде (3.22) –ден табамыз

  2 m  = 2_T,

яғни жиілікті модуляцияланған сигнал спектрі ені екі еселенген жиілік девиациясына тең болады.

m 1 кішкене мәндерінде, яғни спектр ені 2 - ға жақын , бұл бір тоналды модуляциядағы амплитудалы – модуляцияланған тербелістердікіндей.

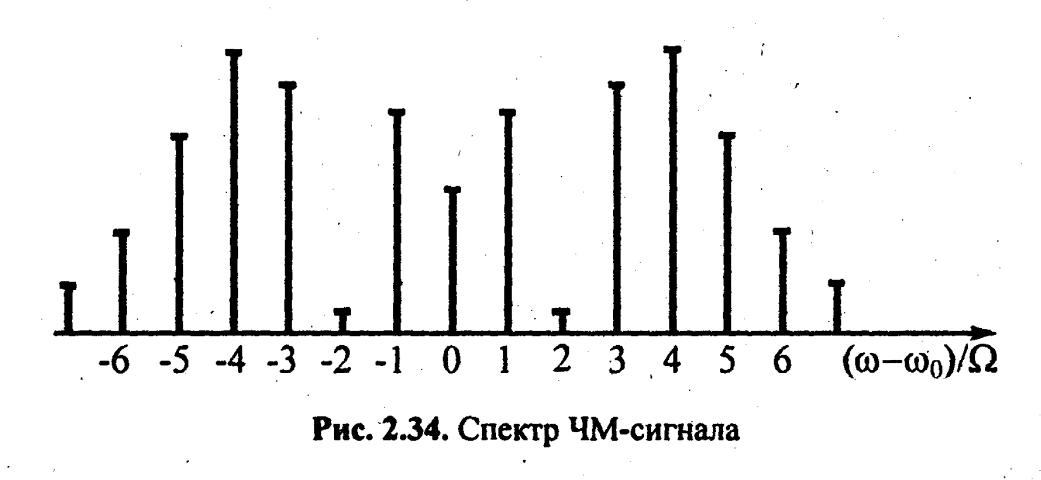
3.8 – сурет. Модуляция индексі m = 3 болғандағы жиіліктік

модуляция спектрі