Амплитудалы модуляцияланған сигналдың энергетикалық сипаттамалары.

Бір тоналды амплитудалы модуляцияланған сигнал көзі гармоникалық тербелістердің үш тізбекті қосылған көздеріне пара-пар:

, негізгі тасымалдаушы тербеліс;

, жоғарғы бүйірлік тербеліс;

, төменгі бүйірлік тербеліс.

Анық болуы үшін тізбекті қосылған ЭҚК көздері бір ОМдық резисторға жүктемеленген дейік. Сонда амплитудалы модуляцияланған сигналдың ілездік қуаты қосынды кернеулердің квадратына тең болады.

.

Мұнда, u_тас - тасымалданушы сигнал амплитудасы, u_жб -жоғарғы бүйірлік жиілікті сигнал құрастырушысы амплитудасы, u_тб - төменгі бүйірлік жиілікті сигнал құрастырушысы амплитудасы. Бұл өрнекте сигнал көздерінің өзіндік қуаттарымен қатар, ілездік кернеулердің қосталған көбейтіндісіне тең өзара қуаттар да бар. Сигналдың орташа қуатын табу үшін р(t) шамасын жеткілікті үлкен уақыт аралығы Т бойынша орташалау керек:

р_амп  = р_тас  + [р_жб +р_тб ] = .

осыдан табамыз

[p_жб + p_тб]/p_тас = М²/2.

Сөйтіп, тіпті 100% модуляция кезінде де (М=1), екі бүйірлік тербелістердің қуаттары үлесі модуляцияланбаған тасымалдаушы тербелістің қуатының бар болғаны 50% - тін құрайды. Хабар туралы ақпарат бүйірлік тербелістерде екенін ескерсек, амплитудалы модуляцияланған сигналды таратқанда қуаттың тиімсіз пайдаланылуын көреміз.

Күрделі модуляцияланған сигналдағы амплитудалық модуляция.

Іс жүзінде бір тоналды амплитудалы модуляцияланған сигналдар сирек қолданылады. Көбінесе модуляциялайтын төменгі жиілікті сигналдың күрделі спектралдық құрамы бар. Осындай сигналдың математикалық моделі тригонометриялық қосынды қатар табылады.

(3.10)

мұнда жиіліктер реттелген өсіп отыратын қатарды құрайды, ал бұл жағдайда _і амплитудалар мен Ф_і фазалар ерікті түрде өзгереді (3.7) формуласын (3.5) –ке қойып табамыз

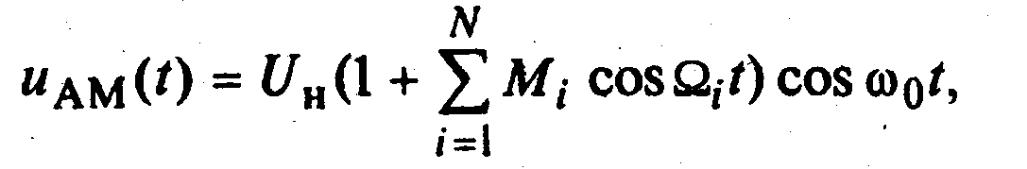(3.11)

мұнда M_i = k_AE_i/U_н - парциальды (бөлінді) модуляция коэффициенттері жиынтығы.

Бұл коэффициенттер күрделі модуляциялайтын сигналдың жеке гармоникалық құрастырушыларының алынған жоғары жиілікті модуляцияланған тербелістің амплитудасының жалпы өзгерісіне әсерін сипаттайды.

Екі косинустың көбейтіндісінің тригонометриялық формуласын пайдалана отырып, күрделі емес түрлендірулер жасап, (3.8) өрнегін келесі түрде жазамыз:

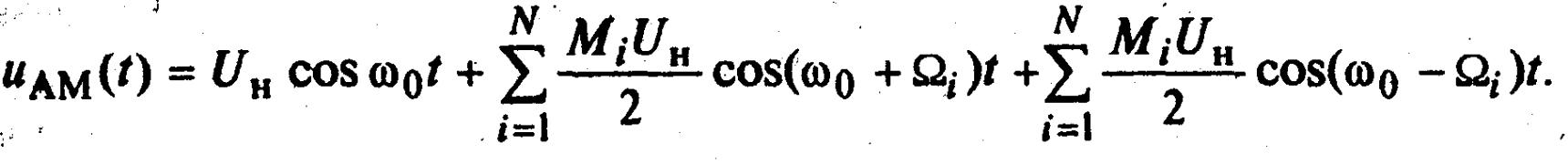(3.12)

(3.12) –ден көрініп тұр, күрделі амплитудалы – модуляцияланған сигналдың спектрінде, тасымалдаушы тербеліспен қатар, модуляциялайтын сигналдың масштабты көшірмелері болып табылатын және ₀ тасымалдаушы жиілікке қарағанда симметриялы орналасқан жоғарғы және төменгі бүйірлік құрастырушылар тобы бар. Осыдан маңызды қорытынды шығып тұр: күрделі амплитудалы модуляцияланған сигналдың спектрі ені модуляциялайтын сигналдың спектрінің ең жоғары жиілігі _N –мәніне тең.

Мысал ретінде 3.4 -суретте үш тоналды (үш әртүрлі гармоникадан тұратын) модуляциялайтын сигналдың S_е() және оған сәйкесті амплитудалы модуляцияланған сигналдың S_АМП() спектралдық диаграммалары (3.5- сурет) көрсетілген.

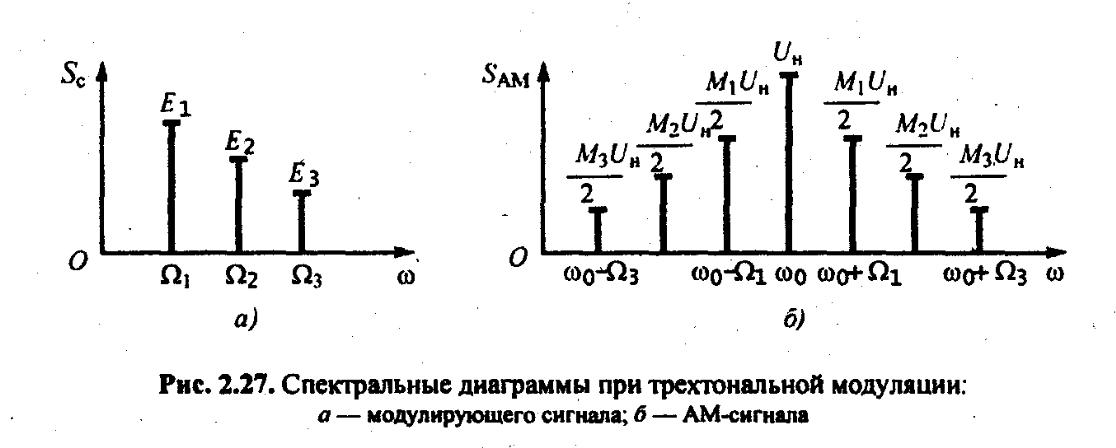
3.4 - сурет. 3.5 - сурет

(3.12) формуласына сәйкес Осы модуляциялайтын сигналға сәйкесті S(t) модуляциялайтын сигнал көптоналды амплитудалы модуляцияланған

спектралдық диаграммасы сигнал спектралдық диаграммасы

Сонымен, күрделі модуляцияланған амплитудалы модуляцияланған сигнал спектрінде тасымалдаушы тербелістен басқа жоғарғы және төменгі бүйірлік тербелістер топтары бар. Жоғарғы бүйірлік жиіліктер облысына ₀ шамасына ығысқан модуляциялайтын сигнал спектрінің масштабы копиясы болып табылады. Төменгі бүйірлік тербелістер спектрі де S(t) сигналдың спектралдық диаграммасын қайталайды, бірақ тасымалдаушы жиілік ₀ –ға қарағанда айнадан шағылысқандай орналасады.

Амплитудалы манипуляцияланған сигналдар.

Көптоналды амплитудалы-модуляцияланған сигналдардың маңызды бір түрі болып манипуляцияланған сигналдар есептелінеді. Қарапайым жағдайда бұлар бір-бірінен үзілісті бөлінген радиоимпульстардың тізбегі болып табылады(3.6 - сурет).

Мұндай сигналдар радиотелеграфияда және радиоарналар бойымен дискреттік ақпаратты тарату жүйелерінде пайдаланылады.

Егер s(t) сәтінде не 0, немесе 1 мәнін қабылдайтын функция болса, онда

3.6 –сурет. Амплитудалы манипуляцияланған сигналдың

осциллограммасы

амплитудалы – манипуляцияланған сигнал мына түрде беріледі

u_ман (t) = U_m s(t) cos (₀t + ₀). (3.13)

Мысалы s(t) функциясы видеоимпульстардың периодты тізбегін бейнелейді дейік. Осы импульстардың амплитудасы А =1 (3.10) негізінде ₀ = 0 болғанда аламыз:

,

мұнда q- импульстер қуыстылығы.