5. Транспортна задача

Транспортна задача — це специфічна задача лінійного про­грамування, застосовувана для визначення найекономічнішого плану перевезення однорідної продукції від постачальників до споживачів.

Математична модель транспортної задачі має такий вигляд:

(5.1)

за обмежень

(5.2)

(5.3)

, (5.4)

де х_ij — кількість продукції, що перевозиться від i-го постачаль­ника до j-го споживача;

с_ij — вартість перевезення одиниці про­дукції від i-го постачальника до j-го споживача;

а_i — запаси про­дукції i-го постачальника;

b_j — попит на продукцію j-го споживача.

Алгоритм розв’язання транспортної задачі представлено на рис.5.1.

Рисунок 5.1 – Розв’язок транспортної задачі

Методи пошуку початкових опорних планів транспортної задачі представлені на рис.5.2.

Рисунок 5.2. - Методи пошуку початкових опорних планів транспортної задачі

Метод північно-західного кута

Побудову опорного плану задачі починають із заповнення лівої верхньої клітинки таблиці х11, в яку записують менше з двох чисел а1 та b1.

Далі переходять до наступної клітинки в рядку або в стовпчику і заповнюють її, і т.д. Закінчують заповнювати таблицю у правій нижній клітинці.

Метод потенціалів

При розв’язанні транспортної задачі побудований опорний план може бути досить далеким до оптимального. Тому необхідно:

по-перше, перевірити його на оптимальність,

по-друге, мати механізм його поліпшення, якщо план не є оптимальним.

Одним з методів, який дозволяє вирішити наведені завдання, є метод потенціалів.

Поставимо у відповідність кожному постачальнику A_i деяку величину u_i, а кожному споживачеві B_j – величину v_j . Ці величини називаються потенціалами постачальників та споживачів. Перевірка оптимальності базується на наступному твердженні:

Якщо план X*=(x*_ij) є оптимальним, то йому відповідає така система потенціалів (u*_i, v*_j), для якої виконуються умови:

u*_i + v*_j =с_ij для всіх x*_ij >0, (5.5)

u*_i + v*_j ≤с_ij для всіх x*_ij =0, (5.6)

i=1..m, j=1..n.

Перша умова дозволяє відшукати систему потенціалів, а друга - перевірити план на оптимальність. Якщо план не є оптимальним (тобто, хоча б одна з умов порушується), то його поліпшення можна здійснити за рахунок однієї з тих вільних клітин, для якої має місце порушення.

Розглянемо алгоритм методу потенціалів.

1) складається система рівнянь для знаходження потенціалів. Для цього для кожної зайнятої клітини записується рівняння

u_i + v_j =с_ij . (5.7)

В отриманій системі маємо m+n–1 рівнянь і m+n невідомих змінних (потенціалів) . Тому така система має нескінчену кількість розв’язків. Нас задовольнить будь-який з них. Для цього оберемо одне зі значень одного з потенціалів довільним (вільна змінна). Як правило, для спрощення розрахунків, його обирають рівним нулю. Вибір змінної ніякого впливу на кінцевий результат не має, однак її обирають виходячи зі зручності подальших обчислень. Наприклад, в ролі вільної змінної обирають таку змінну, яка входить в найбільшу кількість рівнянь.

2) для кожної вільної клітини знаходяться величини

_ij = c_ij – (u_i + v_j). (5.8)

Якщо серед отриманих величин є від’ємні, план не є оптимальним, і його можна поліпшити.

Це здійснюється за рахунок включення у план тих клітин, (перевезень), для яких отримані від’ємні значення. Якщо всі значення оцінок _ij невід’ємні, то отриманий план є оптимальним. При цьому нульове значення величини _ij свідчить про те, що дану клітину також можна включити у план з відповідними перерахунками, однак загальна вартість перевезень при цьому не зміниться. Тобто, ми будемо мати ще один (або декілька) оптимальний план. Цей висновок важливий для практичної реалізації, коли з декількох отриманих оптимальних планів потрібно обрати той, який буде задовольняти деяким додатковим умовам.

Приклад 5.1 У двох виробників А1 і A2 є однорідний товар. У виробника А1 — 200 т, у виробника А2 — 160 т. Вказаний товар слідує відвантажити трьом споживачам Bl, B2, В3, потреба яких складає відповідно 140, 90 і 130 т. Відстані від виробника до споживача складають: від виробника А1 — 6, 4 і 2 км, від виробника A2 — 5, 3 і 2 км.

Потрібно скласти план відвантаження товару, за якого транспортні витрати були б мінімальними.

Рішення. У приведеній задачі число пунктів відправлення товару або число постачальників рівне двом, а число споживачів — трьом, тобто m = 2, а n = 3.

Очевидно, що транспортні витрати будуть якнайменшими у тому випадку, коли загальна кількість тонно-километрів буде якнайменшою.

Розташуємо всі дані в табл. 5.1.1.

Таблиця 5.1.1 - Вихідні дані

Виробники	Наявність товару, т	Споживачі та їх потреба у товарі
		В1 =140т	В2 =90т	В3 =130 т
А1	200	6	4	2
А2	160	5	3	2

Табл. 1 дозволяє нам відразу скласти першу програму. Для її отримання ми cкористуємося так званим правилом «північно-західного кута». Суть цього методу полягає в наступному: ми починаємо з відвантаження товару виробником А1 споживачу В1 тобто із заповнення клітинки А1В1, що стоїть в північно-західному кутку нашої таблиці.1. Оскільки наявність товару у виробника А1 більше потреби споживача В1 {а1>bj}, то ми віддаємо споживачу В1 всі необхідні йому 140 т, що залишилися 60 т товару — споживачу В2. Вичерпавши всі можливості виробника A1, переходимо до розподілу товару, що знаходиться у виробника A2. Оскільки попит В1 повністю задоволений, то ми переходимо до споживача В2. Йому відвантажуємо не дістаючих 30 т товару. Що залишилися в A2 130 т віддаємо споживачу В3.

Ми одержуємо першу програму або перший опорний план. При цій програмі транспортні витрати, виражені в тонно-километрах, складуть:

f1= 140x6 + 60x4 + 30x3+ 130x2= 1430 ткм.

Замітимо, що чотири клітинки виявилися заповненими. У нашій задачі число виробників m = 2, а число споживачів n = 3. Число заповнених кліток рівне, таким чином, m + n — 1 = 2 + 3 — 1 = 4.

При побудові будь-якої програми число завантажених кліток повинне бути рівне т + п— 1. Крім того, заповнені клітинки не повинні утворити циклу. Іншими словами, не повинно бути жодного прямокутника, всі вершини якого є заповненими клітинками.

Таблиця 5.1.2 – Застосування методу «північно-західного кута»

Виробники	Наявність товару, т	Споживачі та їх потреба у товарі
		В1 =140т	В2 =90т	В3 =130 т
А1	200	6	4	2
		140	60
А2	160	5	3	2
			30	130

Останню вимогу формулюють іноді ще і так: завантажені клітинки повинні утворити викреслювану комбінацію. Це означає, що ми повинні мати нагоду викреслити всі стовпці і всі рядки, викреслюючи при цьому кожного разу не більш одну завантажену клітинку

Приклад 5.2. На складах А1, А2,А3 міститься однорідна продукція у кількостях відповідно 300, 150, 180т. Споживачі В1, В2, В3, В4 повинні отримати цю продукцію у кількостях 190, 210, 260 і 220 т відповідно.

Визначити такий варіант закріплення постачальників за споживачами, за яким загальні витрати на перевезення будуть мінімальними. Витрати на перевезення 1т продукції задаються матрицею (табл..5.2.1). Знайти план перевезень даної транспортної задачі методом північно-західного кута, що мінімізує їх загальну вартість. Нехай транспортна задача задана наступною таблицею

Таблиця 5.2.1- Вихідні дані

	B1 190	B2 210	B3 260	B4 220
A1 300	9	6	5	4
A2 150	7	6	4	6
A3 180	6	7	6	5

Розв’язок.

Знайдемо сумарні значення запасів вантажу та потреб у ньому.

Отже, розраховані величини не співпадають, тому дана задача є задачею відкритого типу. Щоб звести її до завдання закритого типу, уведемо фіктивного постачальника A₄ з обсягом вантажу, рівного 880– 630= 250 (од). Вартості перевезень від нього до споживачів покладемо рівними нулю в результаті отримаємо наступну таблицю.

Таблиця 5.2.2 – Введення фіктивного виробника А4

В А	B1 190	B2 210	B3 260	B4 220
A1 300	9	6	5	4
A2 150	7	6	4	6
A3 180	6	7	6	5
A4 250	0	0	0	0

Побудуємо опорний план, скориставшись методом мінімального елемента. Заповнення таблиці розпочинаємо з комірок з найменшим значенням вартості. В даному випадку це одна з комірок останнього рядка таблиці 5.2.2. Оберемо комірку (4.1). Оскільки при цьому запаси фіктивного споживача повністю не вичерпані, також буде заповнена ще одна комірка цього рядка, в даному випадку (4.2). Остаточно результати відображені у таблиці 3.3.

Таблиця 5.2.3– Застосування методу мінімального елемента

В А	B1 190	B2 210	B3 260	B4 220
A1 300	9 0	6 0	5 80	4 220
A2 150	7 0	6 0	4 150	6 0
A3 180	6 0	7 150	6 30	5 0
A4 250	0 190	0 60	0 0	0 0

Як видно з цієї таблиці, заповненими є сім клітин, тобто, отриманий план є не виродженим. Загальна величина витрат на перевезення складає W₀=3110 (г.о.)

Перевіримо отриманий план на оптимальність. Для цього скористаємось методом потенціалів.

u₁=0,u₂= –1,u₃= 1,u₄= –6,v₁=6, v₂=6 v₃=5, v₄=4.

D₁₁ = 3; D₁₂ = 0; D₂₁ = 2; D₂₂ = 1; D₂₄ = 3; D₃₁ = –1; D₃₄ = 0; D₄₃ = 1, D₄₄ = 2.

Отже, серед отриманих величин D_ij є від’ємні, отже отриманий план можна поліпшити за рахунок клітини (3.1). Цикл перерахунку в даному випадку має вигляд (3,1) – (3,2) – (4,2) – (4,1). Новий план відображений в таблиці 5.2.4.

Таблиця 5.2.4 – Застосування методу потенціалів

В А	B1 190	B2 210	B3 260	B4 220
A1 300	9 0	6 0	5 80	4 220
A2 150	7 0	6 0	4 150	6 0
A3 180	6 150	7 0	6 30	5 0
A4 250	0 40	0 210	0 0	0 0

Загальні витрати на перевезення зменшаться на 150 г.о. і становитимуть W₁=2960 (г.о.).

Не відображаючи значення потенціалів цього плану, запишемо величини D_ij .

D₁₁ = 4; D₁₂ = 1; D₂₁ = 3; D₂₂ = 2; D₂₄ = 3; D₃₂ = 1; D₃₄ = 0; D₄₃ = 0, D₄₄ = 1.

Отже, отриманий в таблиці 5.2.4 план є оптимальним. Аналізуючи його, можна зробити такі висновки. Споживач B₁ отримує від фіктивного споживача 40 од. вантажу. Тобто, насправді його потреби не будуть задоволені на цю ж кількість одиниць. Аналогічний висновок можна зробити стосовно споживача B₂. В даному випадку його потреби не будуть задовільне ні повністю. Це є недоліком розв’язання завдання, оскільки реальні умови господарювання можуть виключати такий розв’язок. Тоді потрібно обрати інший план, який завідомо буде менш оптимальним.

Наявність нульових значень величин D_ij свідчить про те, що можна побудувати ще один план, який буде рівносильний за сумарною вартістю перевезень побудованому. В даному випадку це можна зробити, включивши у план або клітину (3,4) , або клітину (4,3).

В першому випадку цикл перерахунку має вигляд (3,4) – (3.3) – (1,3) – (1,4), а в другому – (4,3) – (4.10 – (3,1) – (3,3). Як видно, жоден з нових планів не включає в себе комірки другого стовпчика (тобто, інтереси споживача B₂), а тому на описаний вище недолік впливу не здійснюють. Їх можна розглядати лише як альтернативу побудованому плану.

Приклад 5.3. Побудуємо за методом північно-західного кута опорний план задачі. Неважко переконатись, що дана задача є задачею закритого типу.

Перший та другий кроки наведені в таблицях 5.3.1 та 5.3.2, а опорний план – в таблиці 5.3.3.

Значення обсягів перевезень xij запишемо у нижньому правому кутку клітин таблиці. При цьому в останній стовпчик та останній рядок таблиць записуватимемо нові значення запасів та потреб.

Таблиця 5.3.1 – Перший крок методу північно-західного кута

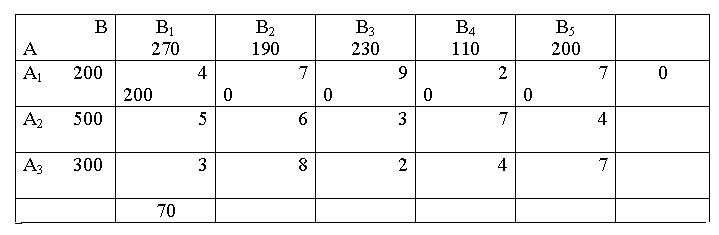
Таблиця 5.3.2 – Другий крок методу північно-західного кута

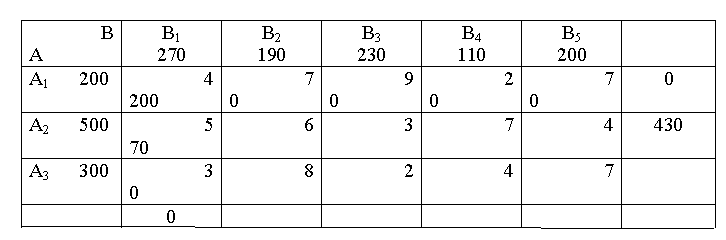
Таблиця 5.3.3 – Опорний план, отриманий за методом північно-західного кута

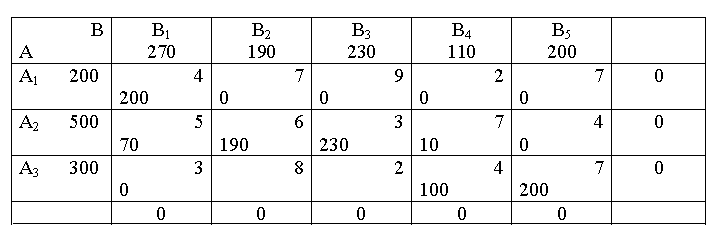
Сумарні витрати на перевезення в даному випадку становлять 4∙200 + 5∙70+6∙190+…+7∙200= 4850(од)

Кількість зайнятих клітин N=7, що свідчить про те, що отриманий план є не виродженим.

Метод мінімальної вартості:

• При включенні до базису пріоритет мають змінні, яким відповідають меншим значенням cij.

• Такий підхід в загальному випадку зменшить сумарну вартість перевезень в опорному плані, а отже, він буде ближчим до оптимального.

• Серед клітин, що залишились, знову знаходиться та, якій відповідає найменша вартість перевезень, і процедура перетворення таблиці повторюється.

• Процес продовжується, доки не буде заповнена вся таблиця, тобто, не вичерпані всі запаси і не задовільнені всі потреби.

Приклад 5.4. Побудуємо за методом мінімальної вартості опорний план задачі, поданої в таблиці 5.1.1. Результати після першого та другого кроків методу а також отриманий опорний план занесемо до таблиць 5.4.1-5.4.3.

Таблиця 5.4.1 – Перший крок методу мінімальної вартості

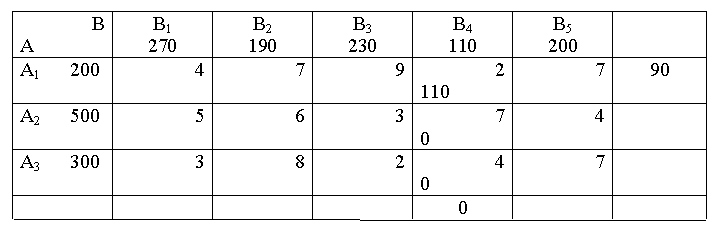
Таблиця 5.4.2 – Другий крок методу мінімальної вартості

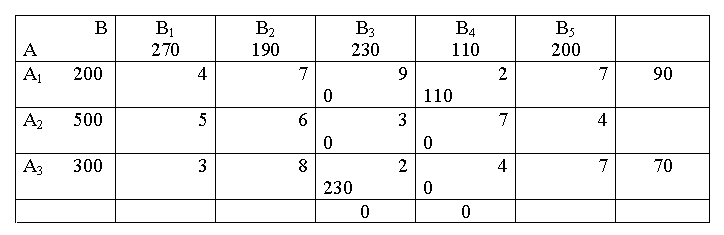
Таблиця 5.4.3 – Опорний план, отриманий за методом мінімальної вартості

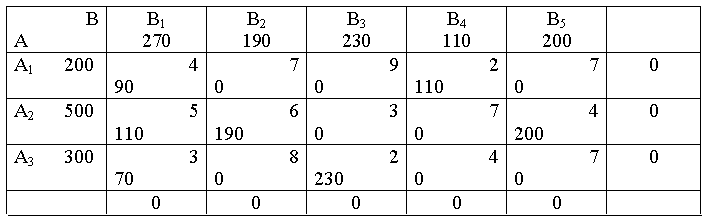
Сумарні витрати на перевезення в даному випадку становлять 4∙90+2∙110+5∙110+…+2∙230 = 3740 (од)

Як бачимо, нами отриманий принципово інший план перевезень. І, виходячи з початкового значення W0 загальної вартості перевезень, він є кращим.

Перевіримо отриманий за методом мінімальної вартості в прикладі 5.4 опорний план на оптимальність за методом потенціалів (таблиця 5.4.3).

Перевіримо отриманий за методом мінімальної вартості опорний план на оптимальність за методом потенціалів.

Для кожної зайнятої клітини запишемо рівняння потенціалів. Отримаємо наступну систему:

В ролі вільної змінної оберемо змінну u₁=0. Тоді з першого рівняння v₁=4, а з другого v₄=2. З третього рівняння знаходимо u₂=5–4=1. Продовжуючи цей процес, знайдемо значення всіх потенціалів.

u₁=0, u₂=1, u₃= –1 v₁=4, v₂=5, v₃=3, v₄=2, v₅=3.

Далі для кожної вільної клітини розрахуємо значення оцінок _ij за формулою (5.8).

₁₂ = 7 – (0+5) = 2; Аналогічно ₁₃ = 6; ₁₅ =4; ₂₃ = –1; ₂₄ = 4; ₃₂ = 4; ₃₄ = 3; ₃₅ = 5.

Як бачимо, серед обчислених величин є від’ємні, отже отриманий план не є оптимальним. Його можна поліпшити за рахунок включення до нього змінної x₂₃. Відповідно, одна зі змінних повинна вийти з опорного плану.

Включення змінної до опорного плану відбувається за таким правилом:

1. Позначимо знаком «+» клітину, яка буде відповідати новій змінній.

2. Далі побудуємо замкнений цикл, який розпочинається і закінчується у цій клітині і проходить лише через зайняті клітини. При цьому зміна маршруту в кожній новій клітині відбувається завжди під кутом 90.

3. Побудова циклу фактично означає, яким чином зміниться обсяг вантажу, який буде перевозитись (зайняті клітини).

4. На кожному кроці включення нової клітини до циклу перерахунку будемо послідовно міняти знак з «+» на «–» і навпаки.

5. Фактично, знак «+» означає, що у відповідних клітинах збільшиться обсяг вантажу, а знак «–» – що зменшиться. Розмір вантажу, що буде переміщуватись, визначається як мінімальне значення величин x_ij для клітин, помічених знаком «–».

6. Такий цикл завжди існує, причому він буде єдиним. Якщо на якомусь кроці далі неможливо обрати зайняту клітину для продовження побудови циклу перерахунку, то потрібно повернутись до попереднього кроку і обрати іншу зайняту клітину.

7. Новий план знову перевіряється на оптимальність за методом потенціалів. При цьому будується нова система потенціалів.

8. Процес завершується, коли серед обчислених оцінок _ij не буде від’ємних.

Таблиця 5.4.4 – Цикл перерахунку для побудови нового плану

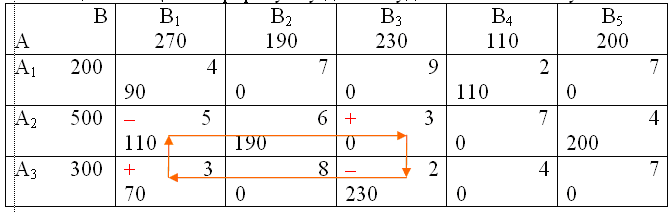
Початковий напрямок визначення маршруту перерахунку ролі не грає, оскільки маршрут завжди буде містити парну кількість клітин.

Таблиця 5.4.5 – Новий план перевезень

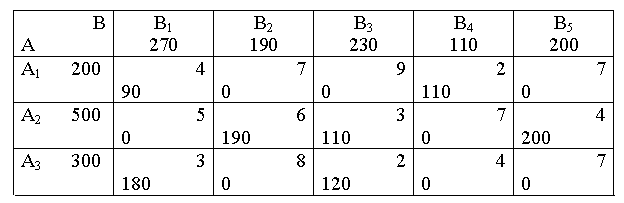
При цьому нова вартість перевезень буде становити W1 = W0 – |D23 |∙x21 = 3740 – 1∙110 = 3630.

П еревіримо новий план на оптимальність. Для цього знову запишемо рівняння потенціалів.

Розв’язок має вигляд: u1=0, u2=0, u3= –1, v1=4, v2=6, v3=3, v4=2, v5=4.

Величини Dij мають наступні значення: D12 = 1; D13 = 6; D15 =3; D21 = 1; D24 = 5; D32 = 3; D34 = 3; D35 = 4.

Оскільки серед отриманих значень Dij немає від’ємних, то побудований в таблиці 3.9 план перевезень є оптимальним.

Розподільчий метод

Сутність методу полягає в тому, що після одержання плану перевезень для кожної вільної клітинки одразу оцінюється можливість її включення до плану з метою зменшення загальної вартості перевезень.

Його перевагою є те, що не проводиться розрахунок допоміжних величин (потенціалів), а для клітинки, що включається до плану, одразу знаходиться можливий маршрут переміщення вантажу.

З іншого боку, пошук маршрутів вимагає певної кількості обчислень, що можна віднести до недоліків методу.

Алгоритм розподільчого методу має наступний вигляд:

1) Для кожної вільної клітинки знаходиться можливий маршрут переміщення вантажу.

При цьому він будується за тими ж правилами, що і для методу потенціалів: він повинен проходити лише через заповнені клітинки; в кожній клітинці повинен змінювати напрямок на 90°, і завершуватись у тій вільній клітинці, з якої він розпочинався. Початкова клітинка позначається знаком «+», а далі клітинки послідовно позначаються знаками «–» та «+».

2) Для цієї клітинки розраховується величина за вартостями тих клітинок, які увійшли до маршруту. При цьому для клітинок, помічених знаком «–», вартості також беруться зі знаком «–». Якщо значення цієї величини менше нуля, то клітинку можна включити до плану перевезень. Якщо всі побудовані оцінки додатні, то отриманий план є оптимальним.

Розглянемо застосування методу для отриманого вище початкового плану за методом мінімальної вартості.

Так, для клітини (1,2) маршрут перерахунку має наступний вигляд: (1,2): (1,2)⁺ – (2,2)^– – (2,1)⁺ – (1,1)^–

Тут також справа зверху біля кожної клітини маршруту вказаний знак, з яким клітина увійшла до маршруту. Тоді D₁₂ = 7 – 6 + 5 – 4 =2

Отже, цю клітину недоцільно включати у новий план, тому що це не призведе до його поліпшення.

Аналогічно розрахуємо маршрути та величини D_ij для інших незаповнених клітин. Результати розрахунків подамо у таблиці 5.4.6.

Таблиця 5.4.6 – Застосування розподільчого методу

Клітинка	Маршрут	Значення Dij
(1,2)	(1,2) – (2,2) – (2,1) – (1,1)	1
(1,3)	(1,3) – (3,3) – (3,1) – (1,1)	6
(1,5)	(1,5) – (2,5) – (2,1) – (1,1)	4
(2,3)	(2,3) – (3,3) – (3,1) – (2,1)	-1
(2,4)	(2,4) – (1,4) – (1,1) – (2,1)	4
(3,2)	(3,2) – (2,2) – (2,1) – (3,1)	4
(3,4)	(3,4) – (1,4) – (1,1) – (3,1)	3
(3,5)	(3,5) – (2,5) – (2,1) – (3,1)	5

Для зручності знаки, з якими клітини увійшли до маршрутів, не відображались. Отже, в новий план потрібно включити клітину (2,3).

Звернемо увагу на те, що значення D_ij вийшли такими ж, як і в методі потенціалів. Тобто, обидва методи дали однаковий результат, що свідчить про їх рівносильність.

Вибір методу, за яким здійснюється перевірка отриманого плану на оптимальність і подальша його оптимізація, рекомендується здійснювати самому користувачеві.