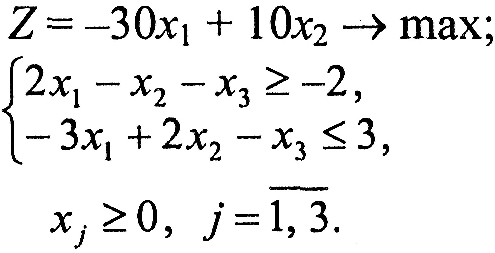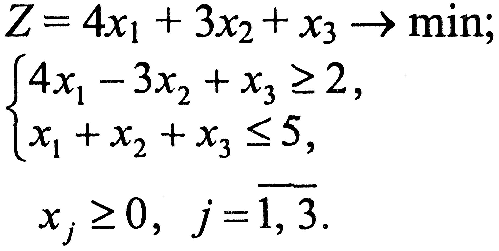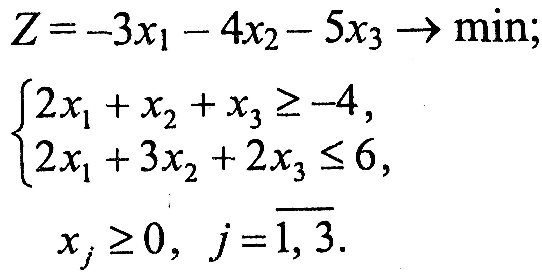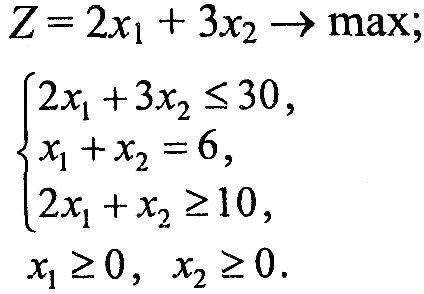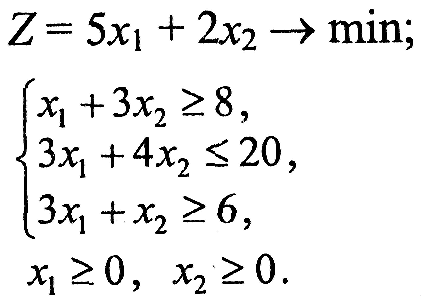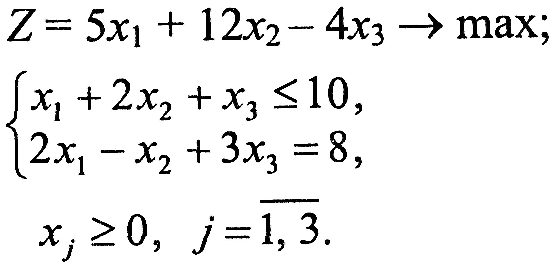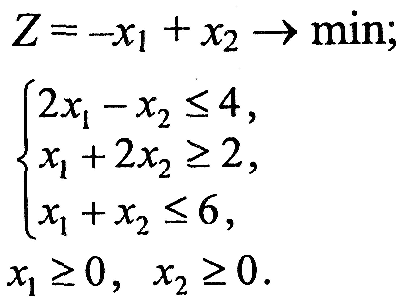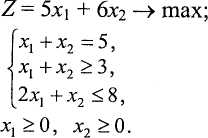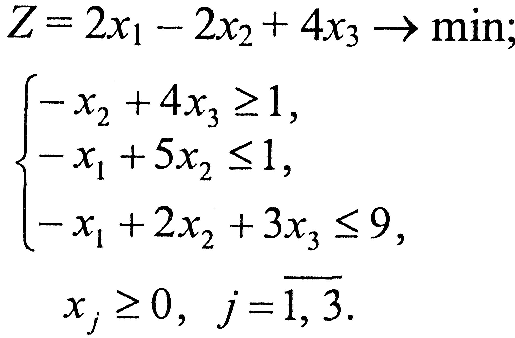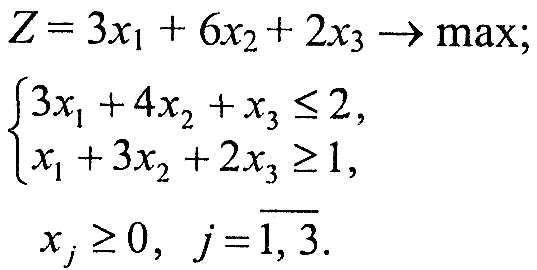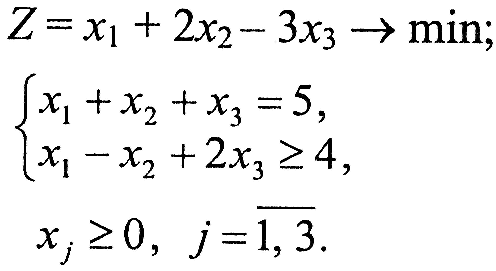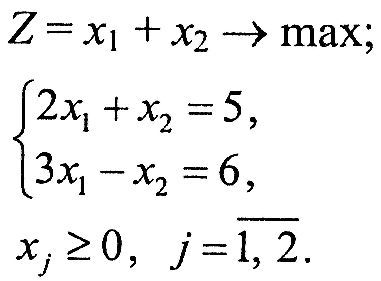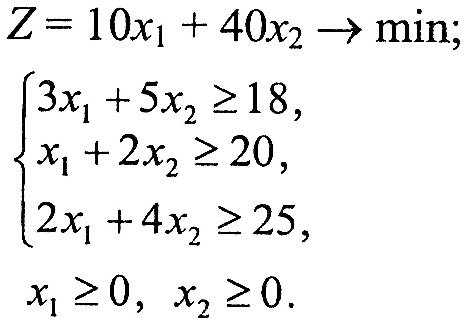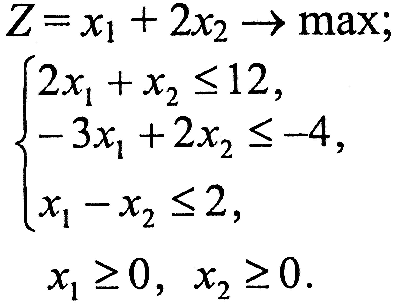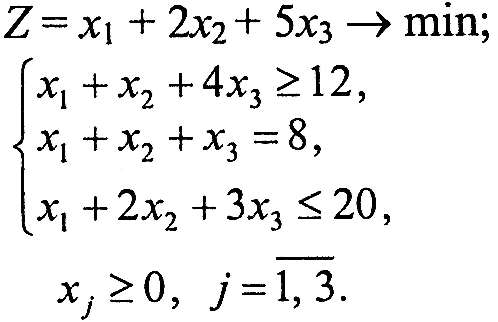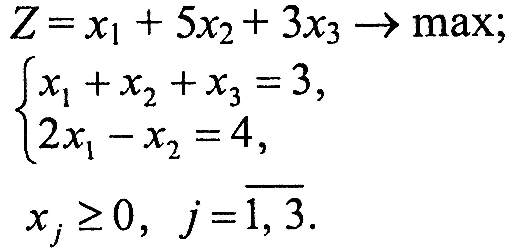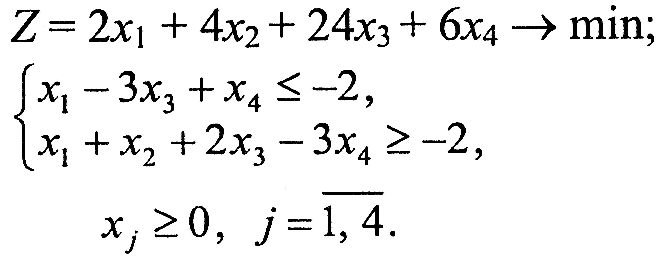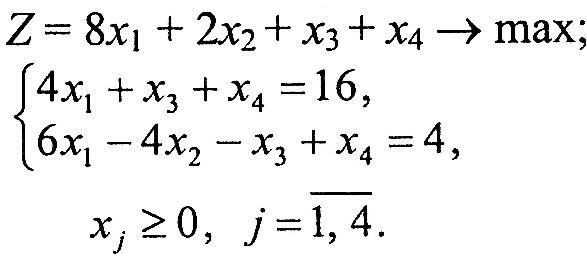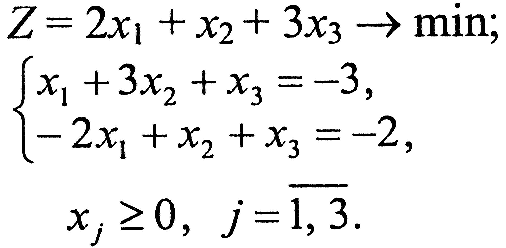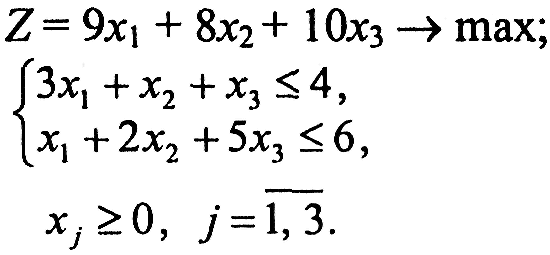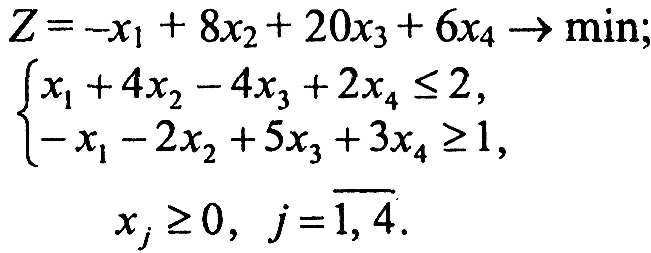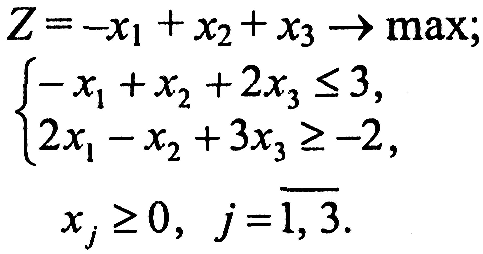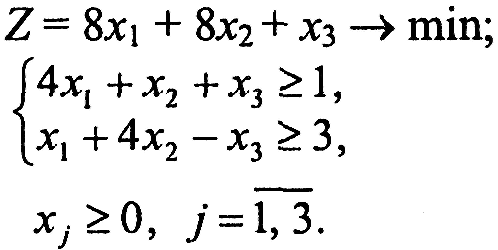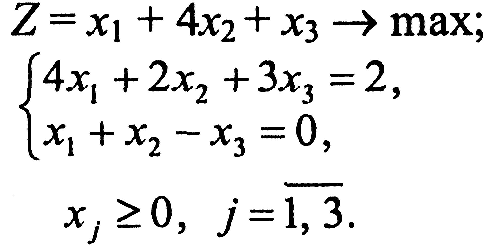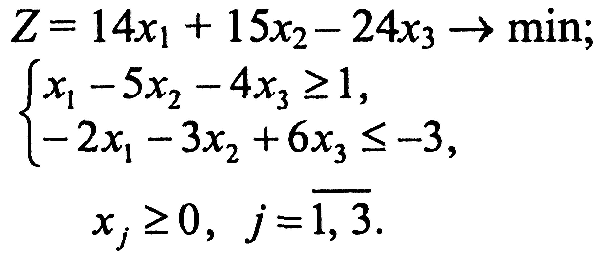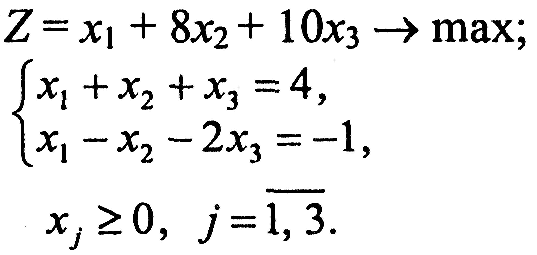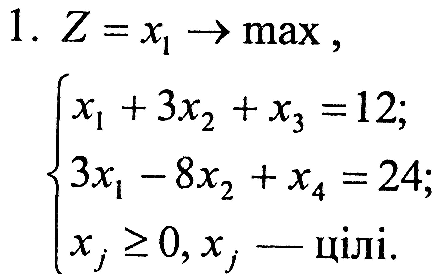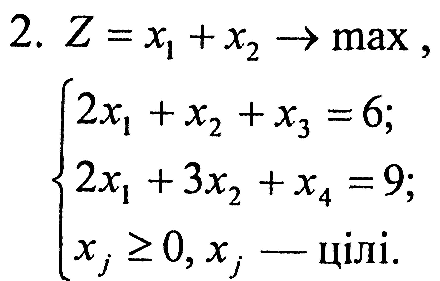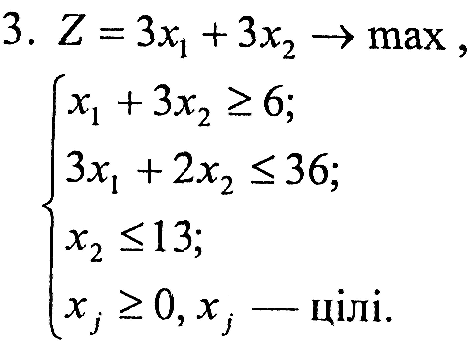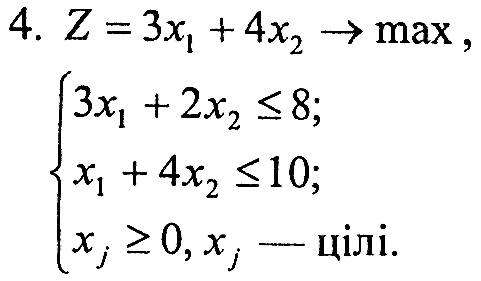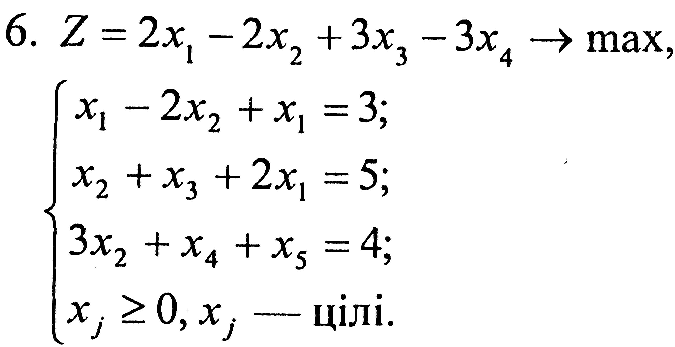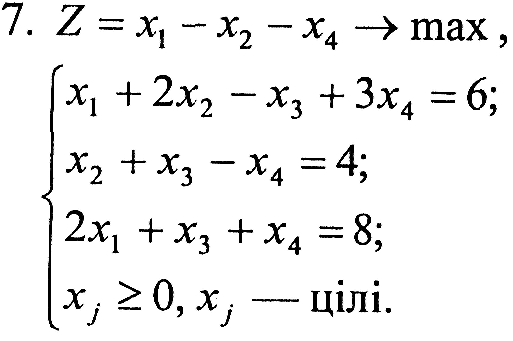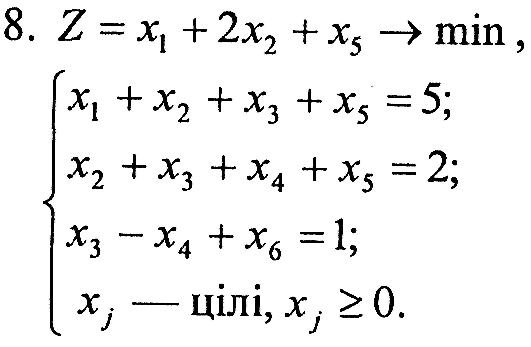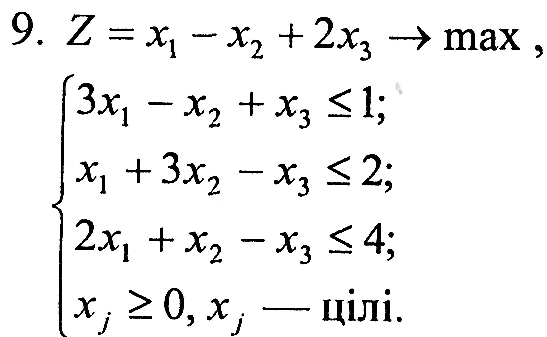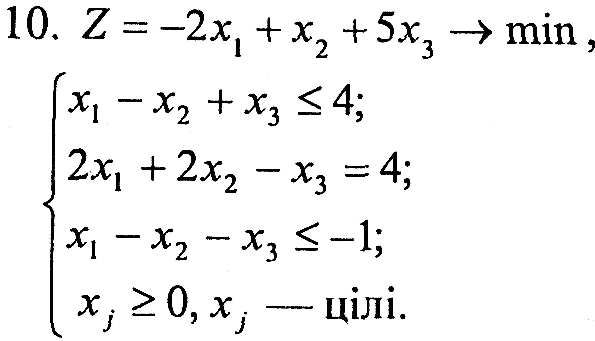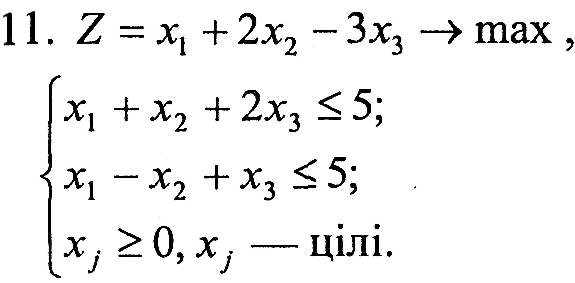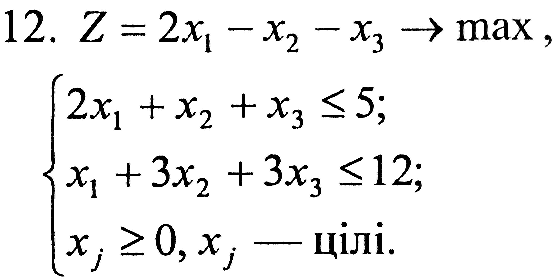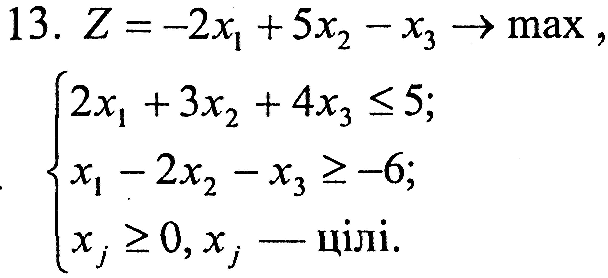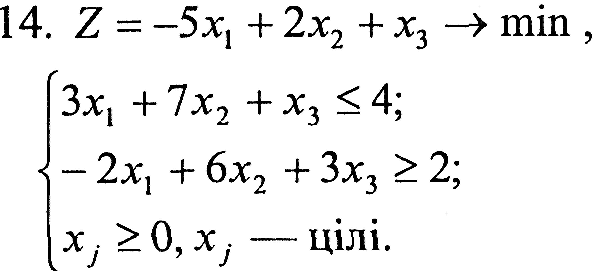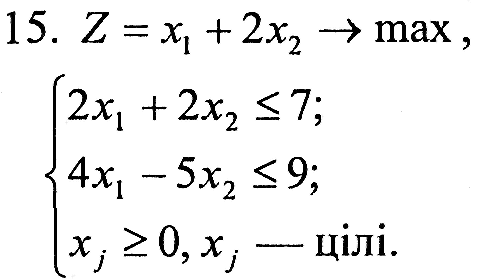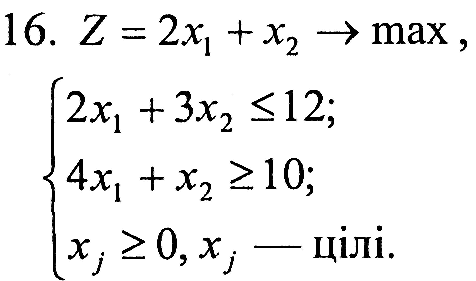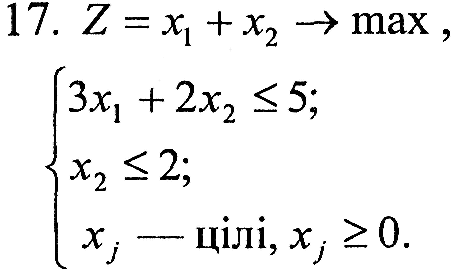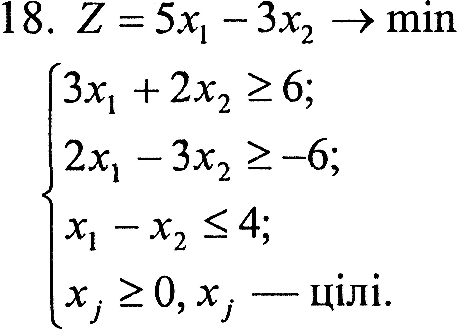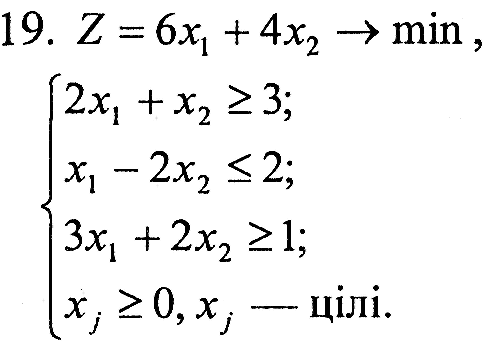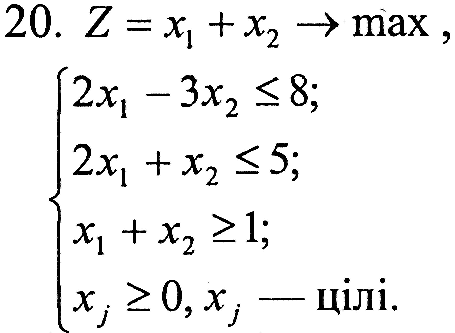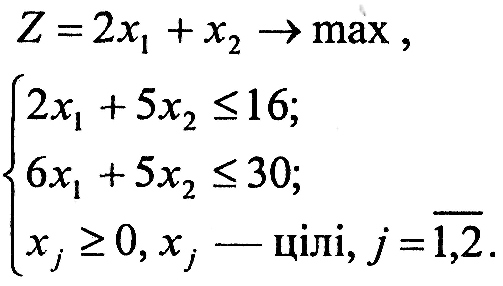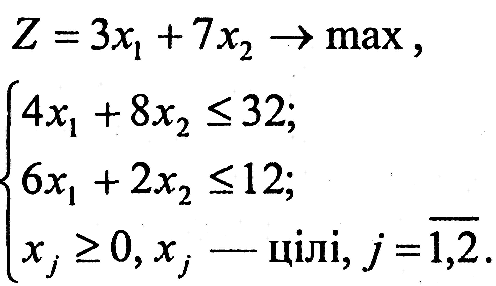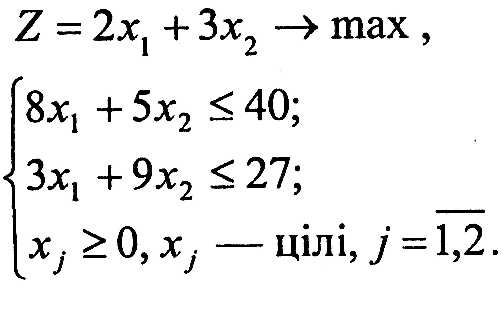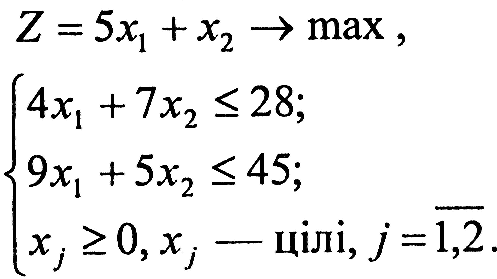Лабораторна робота №6

Теорія двоїстості та цілочислове програмування

Мета роботи: навчитися розв'язувати і аналізувати моделі оптимізаційних та спеціальних задач лінійного програмування.

Використовувані засоби: конспект лекцій, керівництво до даної лабораторної роботи.

Завдання: в процесі виконання лабораторної роботи №6 студенти розв’язують два завдання.

Завдання 1. У наведених задачах (таблиця 6.1) записати двоїсту задачу до поста­вленої задачі лінійного програмування. Розв'язати одну із за­дач симплекс-методом та графічно і визначити оптимальний план іншої задачі.

Таблиця 6.1 – Вихідна інформація до ЛР6

Варіант 1	Варіант 2
Варіант 3	Варіант 4

Продовження таблиці 6.1

Варіант 5	Варіант 6
Варіант 7	Варіант 8
Варіант 9	Варіант 10
Варіант 11	Варіант 12
Варіант 13	Варіант 14
Варіант 15	Варіант 16

Закінчення таблиці 6.1

Варіант 17	Варіант 18
Варіант 19	Варіант 20
Варіант 21		Варіант 22
Варіант 23		Варіант 24
Варіант 25		Варіант 26
Варіант 27		Варіант 28
Варіант 29		Варіант 30

Завдання 2. Відповідно до індивідуального варіанта розв’язати одну із задач (таблиця 6.2) цілочислового програмування: оптимального призначення; про найкоротший шлях; лінійного розкрою; комівояжера; планування виробничої лінії.

Зробити висновки та оформити звіт з лабораторної роботи.

Таблиця 6.2 – Вихідна інформація до ЛР6

Продовження таблиці 6.2

21.	22.
23.	24.
25.	26.
27.	22.
29.	30.

Література: 5,11,13, 30,31

IV. Приклади виконання лабораторних робіт

1. Приклад розв'язування оптимізаційних задач лінійного програмування в середовищі електронних таблиць excel

Оптимальне використання ресурсів при плануванні робіт. Визначення оптимального асортименту

Розрахувати максимальний прибуток цеху від продажу виро­бів А1, А2, АЗ і А4. Ресурси (листи металу, пластмаса, деревина, гроші, трудові ресурси), норми витрат і прибуток від одного ви­робу подано в табл. 1.

Таблиця 1.1 - Оптимальне використання ресурсів при плануванні робіт. Визначення оптимального асортименту

№ з/п	Показник	Запаси ресурсів	Норми витрат
			Виріб А1	Виріб А2	Виріб АЗ	Виріб А4
1	Листи металу (куб. м)	28	2	2	4	5
2	Пластмаса (кг)	10	0	1	2	2
3	Деревина (куб. м)	14	2	1	0	6
4	Прибуток за 1 виріб, грн./шт.		2	4	6	1

Позначимо через х₁ шукану кількість штук виробу А1, а через х₂, х₃ і х₄ відповідно - кількість виробів А2, А3 і А4.

Тоді перше об­меження з використання металу запишеться у вигляді нерівності:

Друге обмеження з використання пластмаси має вигляд:

Третє обмеження з деревини має вигляд:

14

Тоді цільова функція буде такою:

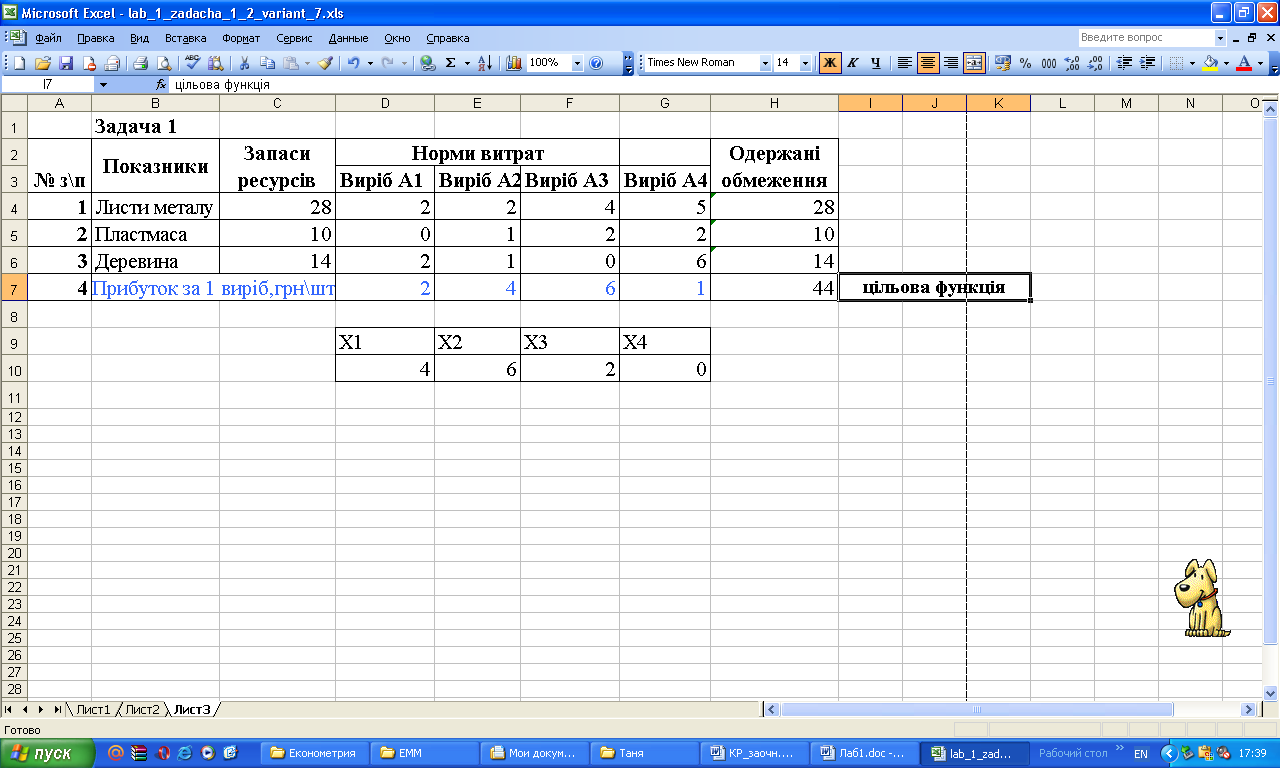
Рисунок 1 - Приклад розв'язання задачі на ПК

Для розв'язання задачі потрібно увійти в додаток Місrоsoft. Ехсеl і виконати послідовно шість етапів.

1. Заповнення таблиці вхідної інформації

Вхідна інформація заноситься в таблицю (рис.1). При цьо­му числові значення показників заносяться в окремі клітинки в ді­апазоні С4:G6.

2. Заповнення діапазону клітинок для незалежних змінних

У розглянутому прикладі для одержання значень незалежних змінних х₁, х₂, х₃ і х₄ обрано діапазон клітинок D10:G10. У цьому діапазоні задамо довільні значення (4, 6, 2, 0).

3. Заповнення клітинки для цільової функції

У діапазоні D7:G7 задані коефіцієнти цільової функції (2, 4, 6, 1).

Формули для визначення значення цільової функції та обме­жень можна ввести відповідно в клітинки Н7, Н4:Н6 звичайним чином або використовуючи функцію СУММПРОИЗВ.

У клітинці Н7 задано функцію СУММПРОИЗВ для визна­чення цільової функції. Для її вибору і роботи з нею зробіть наступне:

1) Клацніть на клітинці Н7, а потім на комірці стандартної панелі інструментів. Відкриється діалогове вікно Мастер функ­цій.

2) Виберіть у списку Категории => Математические, а в списку Функции => СУММПРОИЗВ.

3) Натисніть на кнопку ОК.

Відкриється діалогове вікно СУММПРОИЗВ для введення і визначення сум добутків масивів чисел.

4) Клацніть в полі Массив 1 і введіть діапазон клітинок D7:G7, що відповідає введенню коефіцієнтів цільової функції (4, 6, 2, 0).

5) Клацніть в полі Массив 2 і введіть діапазон клітинок D10:G10, що відповідає введенню незалежних змінних х1, х2, х3, х4.

6) Клацніть на кнопці ОК.

Аналогічні дії слід здійснити і в клітинках Н4:Н6.

4. Зaдання обмежень

У діапазон клітинок С4:С6 уведено коефіцієнти лівих частин обмежень. У клітинки Н4:Н6 введено праві частини (вільні члени) обмежень (28, 10, 14). Для введення лівих частин обмежень обра­но клітинки Н4:Н6. У цих комірках задана функція СУММПРОИЗВ. Для її вибору і роботи з нею потрібно повторити дії, за­значені в пунктах 1 - 6 із Заповнення клітинок для цільової функції.

5. Робота в діалоговому вікні «Поиск решения».

Для роботи в діалоговому вікні «Поиск решения» слід:

1) Вибрати в меню Сервис => Поиск решения. Відкриється діалогове вікно Поиск решения.

2) У полі Установить целевую ввести Н7.

3) Встановити перемикач у поле Равной в положення Мак­симальному значенню.

4) У полі Изменяя ячейки ввести діапазон D10:G10.

5) Задати праві частини обмежень у такий спосіб. У діалого­вому вікні Поиск решения клацніть на кнопці Добавить. Від­криється діалогове вікно Добавление ограничений.

• У полі Ссылка на ячейку введіть адресу клітинки з обме­женням (у даному прикладі Н4:Н6). У полі <= введіть необхід­ний знак обмеження, натиснувши на кнопку .

• У полі Обмеження введіть адресу клітинки з лівою части­ною обмеження, клацнувши на ній мишею. У даному прикладі це клітинка С4:С6.

• Клацніть на кнопці Добавить і введіть аналогічно інші обме­ження. Після уведення всіх обмежень клацніть на кнопці ОК.

6) Для встановлення параметрів пошуку розв'язку клацніть на кнопці Параметри діалогового вікна Поиск решения. Від­криється діалогове вікно Параметри поиска решения.

Установіть прапорці в полі Линейная модель і в полі Не отрицательные значення, клацнувши по них мишею.

• У категорії Оценки клацніть в полі Линейная.

• Якщо ви згодні з іншими параметрами, натисніть на кнопці ОК. Відкриється діалогове вікно Поиск решения (рис. 3.5).

7) Клацніть на кнопці Выполнить діалогового вікна Поиск решения. Після закінчення розрахунку з'явиться діалогове вікно Результати поиска решения.

8) Клацніть на кнопці ОК, якщо потрібно зберегти знайдений розв'язок.

9) Клацніть в полі Восстановить исходные значення, якщо по­трібно перейти до розв'язування іншої задачі лінійного програмування.

6. Аналіз розв'язку задачі

Аналізуючи розв'язок задачі, можна зробити такі висновки.

1. Оптимальний (максимальний) прибуток від реалізації ста­новить 44 грн.

2. Оптимальне сполучення асортименту таке: виріб А1 - 4 шт.; виріб А2 - 6 шт.; виріб АЗ - 2 шт.; виріб А4 - 0 шт.

2. Приклад визначення оптимальності в умовах не визначеності та ризику

Припустимо, що фірма вирішила збудувати готель потрібно прийняти рішення/стратегію: на скільки місць будувати цей готель (х_і = 20, 40, 60). Результат (реалізація вигляді кількості замовлених (зайнятих) місць Х_рj теж задається, наприклад, цифрами Х_рj = 0, 10, 15, 20, 40, 60. Складають кошторис для будівництва готелю та розраховують очікуваний прибуток (табл. 2.1) у залежності від кількості наявних місць у готелі (стратегії будівництва) і кількості дійсь замовлених (заповнених) кімнат - результату експлуатації. Якщо кількість замовлень більша за їх наявність, то тоді корисність не збільшується (бо замовленням відмовляють).

Таблиця 2.1 - Прибуток при експлуатації готелю у залежності від стратегії (загальної кількості кімнат) та кількості замовлених кімнат

Стратегія хі	Результат: замовлені кімнати
	0	10	5	20	40	60
20	-39	52	143	224	224	224
40	-63	28	120	190	405	405
60	-87	5	98	170	365	652

Розглянемо на цьому прикладі використання критеріїв.

Критерій Вальда (обережного спостерігача) оптимізує корисність за припущенням, що середовище знаходиться в найбільш невигідному для спостерігача стані:

- для кожного рядка (стратегії/рішення) обирають мінімальне значення корисності:-39;-63;-87;

-з обраних корисностей обирають максимальне значення (-39), яке і є вирішенням проблеми, бо визначає кількість кімнат Хопт= 20.

Але, судячи з результатів, від будівництва готелю слід відмовитися, якщо керуватися критерієм Вальда, бо корисність/прибуток є від'ємною величиною (l_опт = -39).

Критерій Лапласа. Тому що ймовірність виникнення тієї чи іншої ситуації невідома, то будемо вважати, що всі вони рівноймовірні. Тоді для кожного рядка матриці виграшів розраховується середнє арифметичне значення оцінок. Із отриманих середніх величин оптимальним вважається максимальне значення, яке і дозволяє визначити кількість кімнат у майбутньому готелі.

l₁ = 1/6x(-39+52+143+224+224+224)= 1/6x(828)= 138;

l₂ = 1/6х (-63+ 28+ 120+ 190+ 405+ 405)= 1/6х(1085) = 181;

lз = 1/6x(-87 + 5 + 98 +170 + 365 + 652) = 1/6x(1203) = 201.

Максимальне значення корисності lmах = 201, звідки оптимальна кількість кімнат х_опт = 60 кімнат.

Критерій Севіджа (мінімалізація "жалю"). Вважається, що ризик припустимий. Вкладається стільки грошей, скільки не шкода.

"Жаль" - це втрачений прибуток результату при даній стратегії по відношенню до найкращої стратегії (розглядають по колонці табл. 2.2).

Таблиця 2.2 - Таблиця "жалів" до критерію Севіджа

X	Результат
	0	10	15	20	40	60
20	0	0	0	0	-181	-428
40	-24	-24	-23	-34	0	-247
60	-48	-47	-45	-54	-40	0

Початкова таблиця 2.1 перетворюється на нову таблицю 2.2. елементи якої (в межах одного стовпчика) дорівнюють різни між елементами комірок таблиці 2.1 та максимальним значення елемента цієї ж колонки. Таблиця 2.2 є таблицею "жалів". У цій таблиці виконуємо такі дії:

- у кожному рядку обирається найменше значення -428; -247;-54;

-з них обирається максимальне значення оцінки "жалю яке і визначає обрану кількість кімнат:Uтах = —54;х_0ПТ =60 кімнат.

Критерій Гурвіца. Вводиться деякий коефіцієї , який зветься коефіцієнтом оптимізму або коефіцієнтом довіри (вважається, що середовище може знаходитись у найвигіднішому стані з ймовірністю б а найневигіднішому - з ймовірністю 1 -б).

Для кожної стратегії (кожного рядка таблиці 2.1 розглядаються лише дві величини - максимальне l_ітак і мінімальне l_іmіп значення корисності - і розраховують значення (таблиця 2.3):

Таблиця 2.3 Максимальне l_ітак та мінімальне l_іmіп значення корисності

X	lітак	lіmіп
20	224	-39
40	405	-63
60	652	-87

З отриманих для кожного рядка розрахованих величин обирають максимальне значення, яке і вказує потрібну стратегію/рішення. Нехай, наприклад, б= 0,1. Тоді отримуємо для кожного рядка (кожної стратегії):

h₁ = 0,1 • 224 + (1 – 0,1) • (-39) = -12,7;

h₂ = 0,1 • 405 + (1 – 0,1) • (-63) = -16,2;

h₃ = 0,1 • 652 + (1 – 0,1) • (-87) = -13,0.

Згідно з критерієм Гурвіца, треба будувати готель на 20 місць.

Таким чином, ми отримали кількість кімнат: по Вальду х_опт = 20 кімнат; по Лапласу х_опт = 40 кімнат; по Севіджу х_опт = 60 кімнат; по Гурвіцу х_опт = 20 кімнат. Задачею "Виконавця" є створення умов об'єктивності в оцінці стратегічних напрямів за визначеними "Замовником" умовами:

1. Зокрема, якщо навіть мінімальний ризик неприпустимий, то потрібно використовувати критерій Вальда.

2. Якщо ризик припустимий і «Замовник» має намір вкласти стільки коштів, щоб потім не шкодувати, то обирають критерій Севіджа.

З цими особливостями потрібно ознайомити "Замовника".

Обробка експертної інформації. Задача зводиться до визначення об'єктивного рішення із сукупності думок експертів стосовно гіпотези, яка розглядається. Експертні системи відрізняються методами створення експертних груп, організації їх праці, обробки висновків експертів.

.