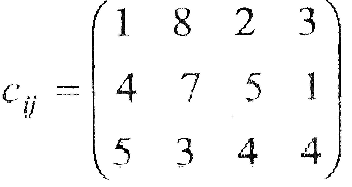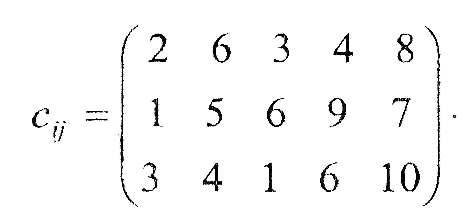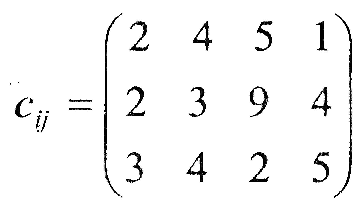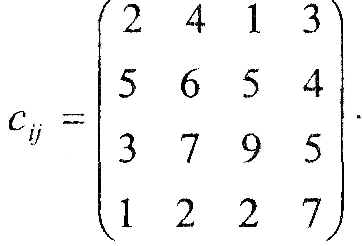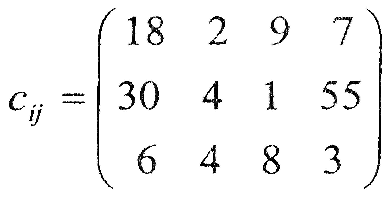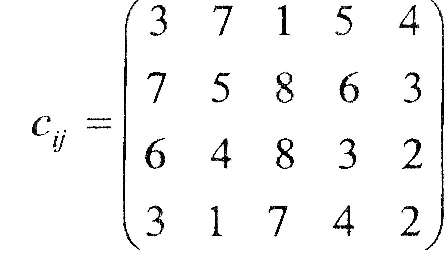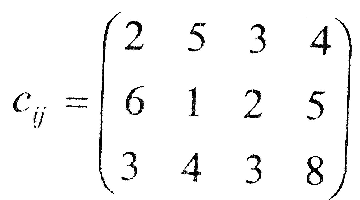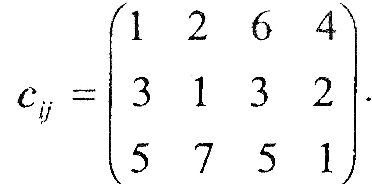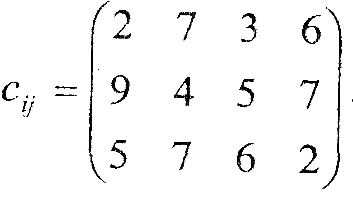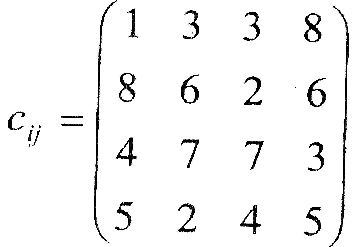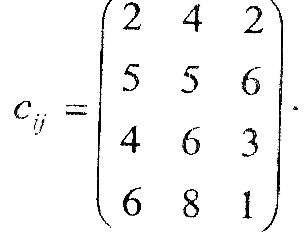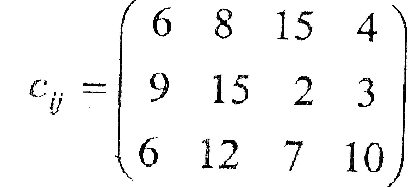Лабораторна робота №3

Графічний метод розв’язування задач лінійного програмування

Мета роботи: навчитися розв'язувати задачі лінійного програмування графічним методом.

Використовувані засоби: конспект лекцій, Microsoft Excel, керівництво до даної лабораторної роботи, файл «лр3.xls».

Завдання: на основі вихідних даних до лабораторної роботи №1 графічним методом знайти найбільше та найменше значення цільової функції в задачі лінійного програмування ЗЛП:

1. Побудувати область обмежень G, вектор-градієнт функції та декілька ліній рівня (перпендикулярних вектору-градієнту).

2. Знайти оптимальні точки області обмежень, в яких цільова функція набуває найбільшого та найменшого значення. Побудувати в цих точках лінії рівня.

3. Обчислити значення цільової функції в оптимальних точках.

4. Зробити висновки та оформити звіт з лабораторної роботи.

Література: 5,11,13, 30,31

Лабораторна робота №4

Симплекс-метод розв’язування задач лінійного програмування

Мета роботи: навчитися розв'язувати задачі лінійного програмування симплексним методом.

Використовувані засоби: конспект лекцій, Microsoft Excel, керівництво до даної лабораторної роботи, файл «лр4.xls».

Завдання: на основі вихідних даних до лабораторної роботи №1 симплексним методом знайти найбільше значення цільової функції в задачі лінійного програмування:

1. Записати задачу лінійного програмування про розподіл ресурсів.

2. Ввести додаткові (надлишкові) змінні та вибрати початковий опорний план.

3. Побудувати послідовність сиплекс-таблиць до досягнення оптимального рішення.

4. Результати розв’язання задачі представити у вигляді діаграми розподілу обсягів випуску видів продукції x₁, x₂ (лінійної, кругової або діаграми будь-якого іншого вигляду).

5. Зробити висновки та оформити звіт з лабораторної роботи.

Література: 5,11,13, 30,31

Лабораторна робота №5

Розв’язування транспортної задачі

Мета роботи: навчитися розв'язувати транспортні задачі.

Використовувані засоби: конспект лекцій, Microsoft Excel, керівництво до даної лабораторної роботи, файл «лр5.xls».

Завдання: на основі даних таблиці 5.1 згідно індивідуального варіанту розв`язати транспортну задачу методами: північно-західного кута; мінімальної вартості; потенціалів.

Побудувати опорний план, скориставшись зазначеними методами та знайти оптимальний план перевезень вантажу, що мінімізує їх загальну вартість.

Для виконання поставленого завдання слід:

1. Записати математичну модель транспортної задачі.

2. Побудувати початковий опорний план методом північно-західного кута або методом мінімального елемента в матриці.

3. Для отриманого опорного плану обчислити потенціали постачальників і споживачів та такі, щоб виконувалась умова (для заповнених клітин розподільчої таблиці) u_i + v_j =с_ij.

4. Обчислити оцінки D_ij = c_ij – (u_i + v_j) для всіх вільних клітин таблиці.

5. Якщо всі оцінки невід`ємні, то отриманий план є оптимальним. У протилежному випадку здійснити перехід до наступного (кращого) опорного плану шляхом перерозподілу поставок за допомогою побудови замкнутого ланцюжка для найбільш перспективної вільної клітини. Для нового плану повторити кроки 3-5 даного алгоритму.

6. Результати розв’язання задачі представити у вигляді плану перевезень та значення загальної вартості перевезень.

7. Зробити висновки та оформити звіт з лабораторної роботи.

Література: 5,11,13, 30,31

Таблиця 5.1 – Вихідна інформація до ЛР5

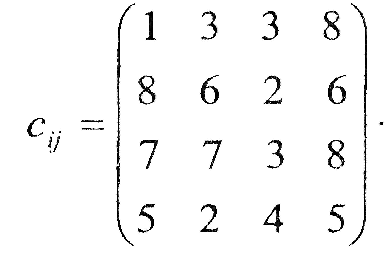
Вартість продукції у постачальників та споживачів	Вартість транспортування продукції
1	2
1. аі. = (30;50;20); bj =(15;15;40;30);
2. аі. = (40;30;35); bj =(20;34;16;10;25);
3. аі =(60;70;20); bj = (40;30;30;50);
4. аі =(30;20;40;50); bj =(35;20;55;30);
5. аі =(68;55;40); bj. =(2;3;3;16);
6. аі = (30;5;45;70); bj =(10;35;15;25;35);

Продовження таблиці 5.1

1	2	1	2
7. аі =(130;90;40); bj =(110;30;50;80;90);		18. аі =(60;70;20); bj = (40;30;30;50);
8. аі = (20;20;40;45); bj =(25;30;40;15);		19. аі =(30;20;40;50); bj =(35;20;55;30);
9. аі =(45;35;70); bj = (20;60;55;45);		20. аі = (40;30;20); bj = (30;25;18;20);
10. аі. =(40;30;50); bj =(20;18;44;75);		21. аі =(68;55;40); bj. =(2;3;3;16);
11. аі =(30;70;50); bj =(10;40;20;60);		22. аі = (30;5;45;70); bj =(10;35;15;25;35);
12. аі =(30;40;70;60); bj =(35;80;25;70);		23. аі =(130;90;40); bj =(110;30;50;80;90);
13. аі =(10;20;35;45); bj =(25;30;40;15);		24. аі = (20;20;40;45); bj =(25;30;40;15);
14. аі =(100;70;70;20); bj =(120;80;60);		25. аі =(45;35;70); bj = (20;60;55;45);
15. аі =(60;130;90); bj=(30;80;60;110);		26. аі. =(40;30;50); bj =(20;18;44;75);
16. аі. = (30;50;20); bj =(15;15;40;30);		27. аі =(30;70;50); bj =(10;40;20;60);
17. аі. = (40;30;35); bj =(20;34;16;10;25);		28. аі =(30;40;70;60); bj =(35;80;25;70);

Закінчення таблиці 5.1

1	2	1	2
29. аі =(10;20;35;45); bj =(25;30;40;15);		30. аі =(100;70;70;20); bj =(120;80;60);