1.9. Расчет замка типа «ласточкин хвост».

Обычно расчет замка ведется на центробежную силу. Составляющая от газовых сил опускается.

При расчете замка типа «ласточкин хвост» определяются:

- нормальное напряжение в сечении I–I диска от центробежных сил лопатки и замкового выступа диска;

- напряжение смятия на площадках контакта лопатки с диском от центробежных сил лопатки;

- напряжение изгиба в клинообразном сечении АВС от центробежных сил лопатки.

Центробежная сила пера и замковой части лопатки Р_ц раскладывается на две силы N, действующие нормально к боковым граням. Пренебрегая силами трения, имеем

=183333/(2·cos20) = 97517 Н.

Сила, действующая на перемычку диска в сечении I–I:

где = 15...20° - угол наклона боковой грани паза к оси лопатки;

β = 360/z = 360/44 = 8,2º – угол между осями лопаток;

Р_цд - цен­тробежная сила одного замкового выступа диска.

, где

м

P_ц.д. = 447,447²·7800·((0,083 + 0,097)/2)·0,002·0,11·(0,427 0,0026)=13,1225 кН

Q = 2·97517·sin(20 + 4,1) + 13,1225 = 79,6 кН

Напряжение растяжения в сечении I-I диска

_p11 = Q/(b·a₁) = 79600/(0,11·0,083) = 8,7 МПа;

Размеры b и a₁ приведены на (рис. 1.4).

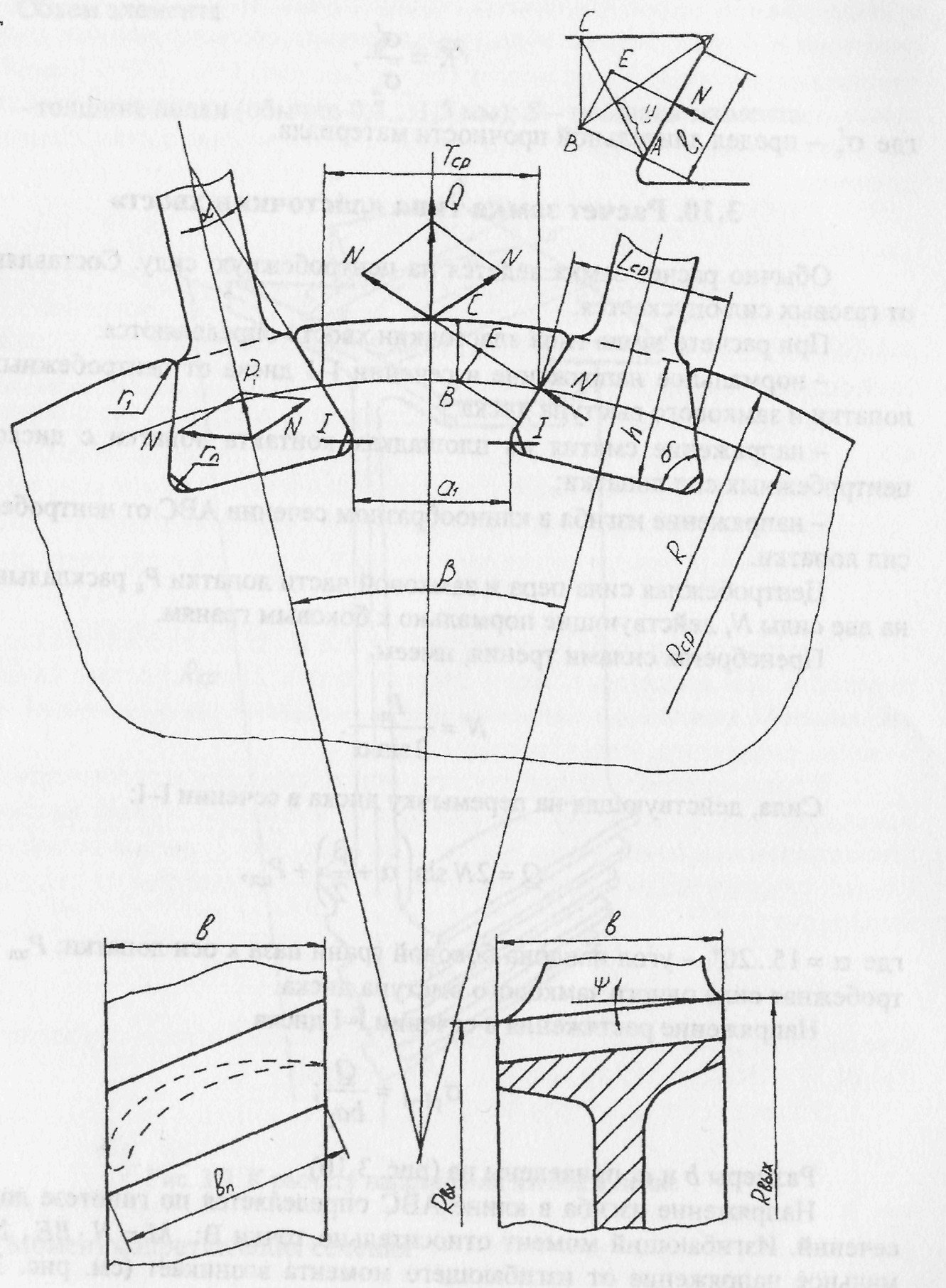
Рис. 1.4. К расчету замка типа «ласточкин хвост»:

β - угол между осями лопаток

Изгибающий момент:

Ми = N·sinɑ·1/3h = 97517·sin(20)·1/3·0,02 = 222 H·м

Макси­мальное напряжение от изгибающего момента возникает (см. рис. 1.4) в точках А и С:

МПа

Напряжение смятия:

_см= 97517/0,11·0,075 =11,8 МПа

Запас прочности в замках типа «ласточкин хвост» по изгибающим на­пряжениям:

К = = 2,3.

2. Расчет на прочность вала гтд

Диаметры вала выберем из условия прочности на кручение

, М_кр=N/,

где М_кр - крутящий момент, кг·см; N - мощность на валу двигателя, кВт; п - частота вращения ротора, с^-1; а - отношение внутреннего диаметра d к наружному диаметру D; τ - касательные напряжения кручения, кг·см².

N = G_г·L_квд =170,507∙519324= 88,5 МВт

М_кр = 88500000/447,447 = 197,8 кН·м

а=0,67

[τ]=360 МПа

D=((16·197800)/(3,14·(10,67⁴)·360000000))^1/3= 0,152 м

d = 0,152·0,67=0,102 м.

3. Расчет на прочность дисков гтд

3.1. Постановка задачи.

Расчет должен включать в себя:

1. Профилирование диска.

2. Поверочный расчет на прочность вращающегося неравномерно на­гретого диска с закрепленными на нем рабочими лопатками, в результате которого в расчетных сечениях диска определяются:

- радиальные и окружные напряжения σ_r и σ_θ;

- эквивалентные напряжения σ_э;

- запас прочности К.

3. Построение графиков изменения по радиусу диска радиальных и окружных напряжений, температуры диска, предельных напряжений и ко­эффициента запаса прочности.

3.2. Исходные данные и принимаемые допущения.

Исходные данные для расчета диска берутся из газодинамического расчета двигателя и расчета на прочность рабочей лопатки, устанавливаемой на рассматриваемом диске.

Такими данными являются:

Р_ц.л = 183,333 кН - центробежная сила массы лопатки;

z = 44 - число лопаток в ободе диска;

r_к = 0,407 м - наружный радиус диска без замковой части;

ω = 447,447 рад/с - частота вращения ротора двигателя;

b = 0,11 — хорда лопатки в корневом сечении;

ρ_л = 8200 кг/м³ ρ_д = 7800 кг/м³ - массовая плотность материала лопатки и диска;

γ = 75^о - конструктивный угол установки лопатки в корневом сечении;

t_{л к} = 309 К - температура рабочей лопатки в корневом сечении;

Для облегчения вывода основных уравнений упругого неравномерно нагретого диска принимается ряд допущений, которые не оказывают замет­ного влияния на точность расчета.

К таким допущениям относятся:

- симметричность диска относительно средней плоскости, перпенди­кулярной оси вращения ротора;

- пренебрежение напряжениями, направленными параллельно оси вращения диска, которые возникают за счет различного давления газа до и после диска;

- температура изменяется только по радиусу и не меняется по толщи­не диска;

- напряжения от вибраций не учитываются, так как определение их составляет специальную задачу.

Указанные допущения позволяют рассматривать напряженное со­стояние диска как плоское.