Теплопроводность стенки

Плоская однослойная стен к а. На рис.6 показана плос­кая однослойная стенка толщиной δ из однородного материала (кир­пича, металла, дерева или любого другого).

П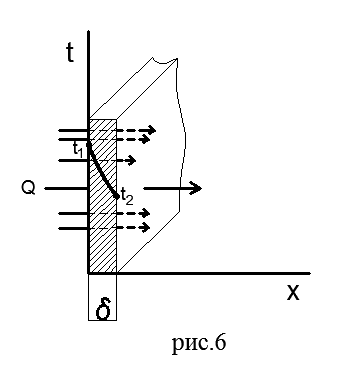 римем, что коэффициент теплопроводности материала λ не зависит от температуры. На наружных поверхно­стях стенки поддерживаются постоянные температуры t₁>t₂ ; температура изме­няется только в направлении оси х, пер­пендикулярной плоскости стенки, т. е. тем­пературное поле одномерно, а градиент температуры равен dt/dx.

Найдем плотность теплового потока, проходящего через заданную стенку, и установим характер изменения темпера­туры по толщине стенки.

Выделим внутри стенки элементарный слой толщиной dx, ограниченный двумя изотермическими поверхностями. Уравне­ние Фурье для этого слоя имеет вид

(52)

Разделив переменные, получим

После интегрирования

Постоянная интегрирования С определяется из граничных усло­вий: при x=0 t = t₁. Отсюда С =t₁ , следовательно, уравнение имеет вид

(53)

Из этого уравнения можно определить плотность теплового по­тока, проходящего через рассматриваемую стенку. Положив в урав­нении (53) х=δ, получим t= t₂, откуда

(54)

Плотность теплового потока в плоской стенке прямо пропорцио­нальна коэффициенту теплопроводности λ, перепаду температур ( ) и обратно пропорциональна толщине стенки δ. Следует иметь в виду, что тепловой поток определяется не абсолютным значением температур, а их разностью — температурным напором Уравнение (54) является расчетной формулой теплопроводности плоской стенки. Оно связывает между собой четыре величины q, λ, δ и :

Зная любые три величины, можно всегда найти четвертую. Отно­шение λ/δ называют тепловой проводимостью стенки; она имеет раз­мерность [вт/(м² • град) ].

Если равенство (54) переписать в другом виде, то получим

(55)

Отношение толщины стенки к коэффициенту теплопроводности δ/λ называют термическим сопротивлением стенки.

Из равенства (55) видно, что удельный тепловой поток прямо пропорционален перепаду температур и обратно пропорционален термическому сопротивлению стенки. Действительно, чем больше знаменатель дроби в уравнении (55), т. е. δ/λ, тем меньше плотность теплового потока q. Следовательно, с увеличением толщины стенки δ или с уменьшением теплопроводности λ уменьшается плотность тепло- ого потока q.

Определив по формуле (54) плотность теплового потока, можно определить общее количество теплоты Q в джоулях, переданное через плоскую стенку поверхностью F за время τ:

(56)

Если в формулу (53) подставить значение q из формулы (54), то можно получить уравнение температурной кривой:

(57)

Это уравнение является уравнением прямой линии. Таким образом, при постоянном значении коэффициента теплопроводности темпера­тура по толщине однородной стенки изменяется линейно. В тех слу­чаях, когда коэффициент теплопроводности зависит от температуры, он является переменной величиной и расчет­ные формулы получаются несколько сложнее.