Занятие № 2. Анализ инвестиционных проектов в MS Excel
В качестве опорного учебного файла используется файл invest.xls. Разработанные функции приведены в файле invest.xls на листе "Ответы c формулами".
Словесную формулировку примеров 1–4 рекомендуется давать под запись, чтобы можно было поработать с файлом invest.xls самостоятельно.
Вопрос №1. Финансовые функции для анализа инвестиционных проектов
Управление инвестиционными процессами представляет собой один из наиболее важных и сложных разделов управления финансами. Принимаемые в этой области решения рассчитаны на длительные периоды времени и им, как правило, присущи следующие аспекты:
а) являются частью стратегии развития фирмы в перспективе;
б) влекут за собой значительные оттоки денежных средств;
в) с определенного момента времени могут стать необратимыми;
г) опираются на прогнозные оценки будущих затрат и доходов.
Одним из ключевых моментов при принятии инвестиционных решений является оценка эффективности предполагаемых вложений. Изученные на предыдущих занятиях методы исчисления характеристик денежных потоков являются тем фундаментом, на котором также базируются и современные методы анализа эффективности инвестиционных проектов. Данные методы можно разбить на две группы: динамические (учитывающие фактор времени) и статические (учетные) (рис. 1).
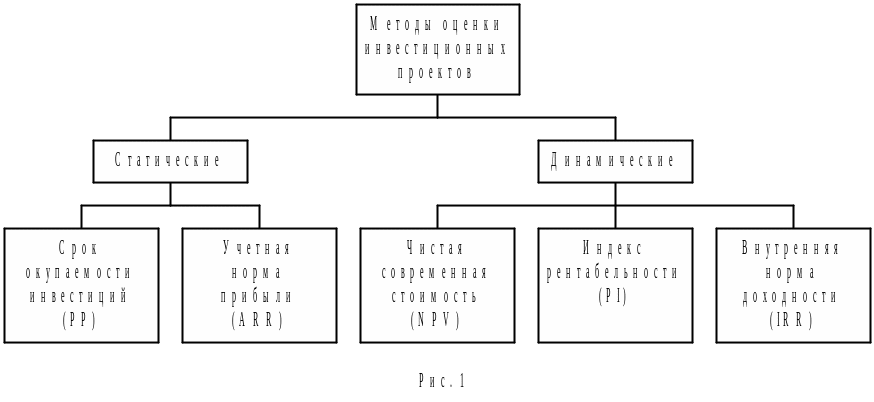
Предмет изучения на сегодняшнем занятии – динамические методы, позволяющие учесть фактор времени, так как они отражают наиболее современные подходы к оценке эффективности инвестиций и преобладают в практике крупных и средних предприятий (банков) развитых стран. В хозяйственной (банковской) практике России применение этих методов обусловлено также и достаточно высоким уровнем инфляции.
Динамические методы часто называют дисконтными, поскольку они базируются на определении современной величины (т. е. на дисконтировании) денежных потоков, связанных с реализацией инвестиционных проектов. Расчет показателей эффективности инвестиционных проектов, базирующихся на дисконтных методах, достаточно трудоемок, поэтому для проведения таких расчетов целесообразно пользоваться программными средствами. В MS Excel подобные расчеты могут быть проведены с использованием ряда финансовых функций, которые можно рассматривать как группу финансовых функций для анализа инвестиционных проектов. К данной группе можно отнести следующие функции MS Excel:
финансовые функции, рассчитывающие показатель чистой современной стоимости (NPV): НПЗ, ЧИСТНЗ;
финансовые функции, рассчитывающие внутреннюю норму доходности (IRR): ВНДОХ, ЧИСТВНДОХ, МВСД1.
Индекс рентабельности (PI) рассчитывается в MS Excel на основании функции НПЗ.
Кроме того, для анализа инвестиционных проектов в MS Excel могут широко использоваться ранее изученные нами инструмент MS Excel "Подбор параметра" и программная надстройка "Поиск решения".
На сегодняшнем занятии будут рассмотрены методы расчета показателей NPV и PI (на основании финансовой функции НПЗ) и ряд прикладных задач финансового анализа, базирующихся на расчете этих показателей.
Метод чистой современной стоимости (NPV)
Основная идея метода чистой современной стоимости (NPV – net present value) в том, чтобы найти разницу между инвестиционными затратами и будущими доходами, выраженную в скорректированной во времени (как правило, к началу реализации проекта) денежной величине.
При заданной норме дисконта можно определить современную величину всех оттоков и притоков денежных средств в течении экономической жизни проекта, а также сопоставить их друг с другом. Результатом такого сопоставления будет положительная или отрицательная величина (чистый приток или чистый отток денежных средств), которая показывает удовлетворяет или нет проект принятой норме дисконта2.
Пусть I0 – сумма первоначальных затрат, т. е. сумма инвестиций на начало проекта; PV – современная стоимость денежного потока на протяжении экономической жизни проекта. Тогда чистая современная стоимость равна:
NPV = PV – I0 . (1)
Величину PV можно определить по формуле (2)
, (2)
где r – норма дисконта;
n – число периодов реализации проекта;
CFt – чистый поток платежей в периоде t.
Подставив формулу (2) в формулу (1), получим:
. (3)
Если рассчитанная таким образом чистая современная стоимость потока платежей имеет положительный знак (NPV > 0), это означает, что в течение своей экономической жизни проект возместит первоначальные затраты I0, обеспечит получение прибыли согласно заданной норме дисконта r, а также её некоторый резерв, равный NPV. Отрицательная величина NPV показывает, что проект убыточен, при NPV = 0 – проект только окупает произведенные затраты, но не приносит дохода.
На примере 1 рассмотрим простейший случай инвестиционных вложений, когда денежный поток проекта состоит из единоразовой суммы первоначальных инвестиций и последующих поступлений средств от его реализации – CFt.
Пример 1
Фирма собирается вложить средства в приобретение нового торгового оборудования, стоимость которого вместе с доставкой, установкой и вводом в эксплуатацию составит 100000 у.е. Ожидается, что внедрение торгового оборудования обеспечит получение на протяжении 6 лет чистых доходов в размере 25000, 30000, 35000, 40000, 45000 и 50000 у.е. соответственно. Принятая норма дисконта равна 10%. Определите экономическую эффективность проекта.
Замечание. Если поступающие платежи реинвестируются в новый проект, то они учитываются в оценке экономической эффективности этого проекта. Если полученные доходы откладываются в виде депозитов в банк, то они в период экономической жизни проекта генерируют поступления, наращенные по банковской процентной ставке.
Решение задачи проведем в среде MS Excel (см. файл invest.xls, пример 1).
Как видим, при условии правильной оценки денежного потока проект обеспечивает возмещение произведенных затрат примерно в конце четвертого года, а по истечении 6 лет обеспечит получение прибыли приблизительно в 57000 у.е.
Пример 1 более эффективно может быть решен с помощью финансовой функции НПЗ, которая реализует соотношение (2). Следует обратить внимание на то, что эта функция не учитывает величину первоначальных затрат I0, т. е. инвестиций, сделанных на момент времени t = 0. Поэтому для определения показателя NPV из полученного результата следует вычесть величину первоначальных вложений I0. Таким образом, можно сказать что функция НПЗ рассчитывает величину PV.
Аргументы функции НПЗ:
аргумент норма – норма дисконта r;
аргументы значения1, значения2… – поток равномерно распределенных во времени платежей CFt.
Как легко заметить, применение функции НПЗ ограничено случаем равномерного распределения платежей во времени. Данное ограничение позволяет преодолеть другая финансовая функция – ЧИСТНЗ, которая является самой мощной в своей группе и позволяет определить показатель NPV для потоков с платежами произвольной величины, осуществляемых за любые промежутки времени. Однако в прогнозных оценках данная функция не имеет существенных преимуществ перед функцией НПЗ, так как в этом случае инвестору, как правило, не известны точные даты поступления платежей.
Наряду с оценочными показателями будущих поступлений на величину NPV существенное влияние оказывает норма дисконта и структура денежного потока. Если влияние нормы дисконта r на величину NPV явно следует из соотношения (3), то влияние структуры денежного потока, на первый взгляд, не является столь очевидным. Влияние указанных величин на величину NPV рассмотрим на примере 1.
Если значение величины r изменить на 20%, то рассматриваемый проект окупится только на шестой год своей экономической жизни; если значение величины r изменить на 30% – в указанный срок проект не окупится.
При r = 30% изменим структуру денежного потока – поступления от проекта будут осуществляться в порядке убывания (для чего отсортируем диапазон ячеек D4:D9 в обратном порядке). Как видим, проект не только становится безубыточным, но и приносит некоторую прибыль уже на пятом году своей жизни. Если изменить значение величины r на 10%, то уже на третьем году жизни проект будет обладать существенным запасом прочности 12700 у.е (сравните с возрастающим потоком, когда после 4 лет жизни проект хоть и является безубыточным, но обладает очень несущественным запасом прочности 1140 у.е).
Показатель NPV считается одним из наиболее корректных измерителей эффективности инвестиционных вложений. Вместе с тем применение абсолютных показателей при анализе проектов с различными исходными данными может приводить к затруднениям при принятии управленческих решений. В этом случае, наряду с абсолютным показателем NPV, применяется относительные показатели – индекс рентабельности проекта PI (profitability index) и внутренняя норма доходности IRR (internal rate of return).
Индекс рентабельности проекта (PI)