Приклад 4.

Н а консолі мостової балки діють дві рівні та паралельні сили F = F' = 30 кН. Визначити реакції опор балки. Вагу балки не враховувати.

Розв'язання:

На балку діє пара сил - F і F' яка прагне обернути її за рухом стрілки годинни­ка. Так як балка у стані рівноваги, то момент актив­ної пари (М_А) бу­де зрівноважуватись моментом, який утворюють опорні реакції М_Р

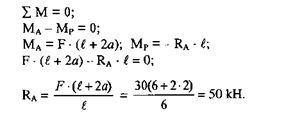
Відповідь: R_в = R_А = 50 кН.

Приклад 5.

В изначити момент тягового зусилля F_т = 200 Н веду­чого автомобільного колеса відносно точки контакту колеса з поверхньою дороги.

Радіус колеса R = 0,35 м.

М_А (F_т) = Fт • R = 200 • 0,35= 70 Нм.

Приклад 6.

В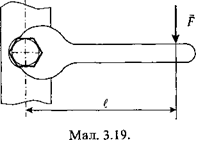 изначити величину моменту, який розвиває робітник при закручуванні гайки, якщо сила натискування на ключ дорівнює F = 150 Н, а довжина ключа l = 20 см.

Шуканий момент дорівнюватиме

М = F ∙ l = 150 • 0,2 = 300 Нм.

Приклад 7.

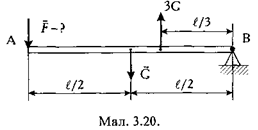
Важіль АВ може обертатися навколо точки закріплення. Вагу важеля G = 20 Н прикладено посередині його. На віддалі 1/3 довжини важеля від точки опори прикладено вертикально вгору силу в рази більшу від ваги важеля. Знайти силу F, яку треба прикласти на кінці А важеля для його рівноваги.

Розв’язання:

Умова рівноваги для важеля матиме вигляд

Відповідь: F =10 H.

Приклад 8.

Для пересувного крана розрахувати противагу G₂ так, щоб кран не перекидався при навантаженні Q = 80 кНм. Вага крана G₁ = 30 кН. Кран установлено на опорах А та В.

Р озв'язання:

Складаємо рівняння рі­вноваги крана

ΣМ_В( ) = 0;

- G₁• (2,5 - 1,5 - 0,4) - G₂ • 2,5 + Q • (4 - 0,6) =0;

- G₁ • 0,6 - G₂ • 2,5 + Q • 3,4 =0;

G₂ = (Q • 3,4 – G₁ • 0,6)/2,5 = (80 • 3,4 - 30 • 0,6)/2,5 = 101,6 кН

Відповідь: G₂> 101,6 kH.

Контрольні питання (завдання):

1. Дайте визначення пари сил.

2. Як визначити момент пари? Правило знаків моменту пари.

3. Які одиниці вимірювання моменту пари?

4. Чи можна переносити пару у площині дії пари?

5. Які пари називаються еквівалентними?

6. Чому дорівнює проекція пари сил на вісь?

7. Як визначити момент рівнодійної пари?

8. У чому полягає умова рівноваги пар?

9. Дайте визначення моменту сили відносно точки?

10. Чому дорівнює момент сили відносно точки, яка лежить на лінії дії сили?

11. Парою сил називається система двох сил:

A). Рівних за модулем, паралельних і протилежно спрямованих;

Б). Які лежать в одній площині;

В). Рівних за модулем, розташованих довільно;

Г). Рівних за модулем і перпендикулярно розташованих.

12. Чим характеризується пара сил (F1, F2)?

A). Рівнодійною R = F1 + F2;

Б). Плечем пари h;

В). Моментом пари F1•h;

Г). Площиною дії пари.

13. Плече пари сил - це:

A). Відрізок, який з’єднує точки прикладання сил;

Б). Найкоротша відстань між лініями дії сил;

В). Будь-який відрізок, який перетинає лінії дії сил;

Г). Відрізок, який з’єднує середини векторів сил.

14. З а якою формулою визначиться момент пари сил М(F; F´), зображеної на малюнку

А). М = АВ∙F.

Б). М = АС∙F.

В). М = - АВ∙F.

Г). М = - АС∙F.

15. Визначити момент пари сил P1 = P2 = 2 H, якщо АВ = 1 м:

А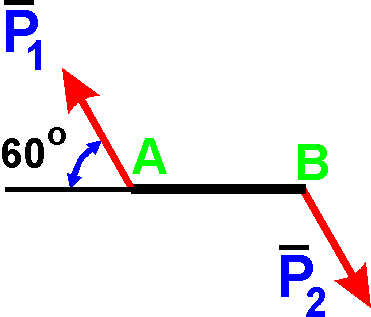 ). -1 H·м;

Б). -1,73 H·м;

В). -2 H·м;

Г). -3·1,73 H·м.

16. Які пари сил є еквівалентними

А). Пари, що мають рівні складові сил.

Б). Пари, лежать в одній площині.

В). Пари, що мають однакові плечі.

Г). Пари, моменти яких однакові.

17. Яка система пар, що діє на тіло буде знаходиться в рівновазі

А)М₁=500Н·м; М₂=200Н·м; М₃=100Н·м

Б) М₁=500Н·м; М₂=-200Н·м; М₃=300Н·м

В) М₁=500Н·м; М₂= -200Н·м; М₃= -300Н·м

Г) М₁=500Н·м; М₂=200Н·м; М₃=300Н·м

18. За якої умови пари сил, розміщені у площині, взаємно врівноважуються

А). Якщо геометрична сума їх моментів дорівнює нулю.

Б). Якщо алгебраїчна сума їх моментів дорівнює нулю.

В). Якщо моменти всіх сил рівні між собою.

Г). У будь-якому випадку.

19. Укажіть правильне закінчення твердження:

Задану пару сил, не змінюючи її дії на тверде тіло,…

А). … можна переносити у будь-яку площину, паралельну площині дії пари.

Б). … можна переносити у будь-яку площину, що проходить крізь лінію дії однієї із сил пари.

В). … не можна переносити у просторі

Г). … можна переносити тільки у площині дії пари.

20. Чи можливо змінювати плече пари сил, зберігаючи неизмінним стан твердого тіла?

A). Ні, при цьому зміниться стан тіла;

Б). Ні, плече пари неможна змінювати ні в якому разі;

В). Так, якщо момент пари не змінеться;

Г). Так, якщо не змінювати модулі сил, які утворюють пару

2 1. Яким повинен бути момент зрівноважуючої пари сил M₃, якщо дани пари сил з моментами M₁ = 28 Н·м і M₂ = 38 Н·м:

A). -10 H·м;

Б). 10 H·м;

В). -66 H·м;

Г). 66 H·м.

22. Момент пари дорівнює 10 Н·м. Чому дорівнює її проекція на вісь

А) 10 Н·м

Б) 0

В) 20 Н·м

Г) -10 Н·м

23. Плечем сили відносно центра називається:

A). Відрізок, який з’єднує центр і точку прикладання сили;

Б). Найкоротша відстань від центру до лінії дії сили;

В). Відрізок, який з’єднує центр і кінець вектора сили;

Г). Відрізок, який з’єднує центр і будь-яку точку вектора сили.

24. В якому випадку момент сили F відносно центра О дорівнює нулю

А). Якщо крім сили F на тіло в довільній точці діє ще одна сила протилежного напрямку.

Б). Якщо лінія дії сили F проходить крізь точку О.

В). Якщо вектор сили F і точка О лежать в одній площині.

Г). Якщо перпендикуляр, проведений з точки О на лінію дії сили F, проходить крізь точку прикладання сили.

25. На важіль АВ діє пара сил з моментом

М = 3 Н·м і сила F. Визначити значення сили F, при якій важіль знаходиться у рівновазі,якщо OА = 2 м:

А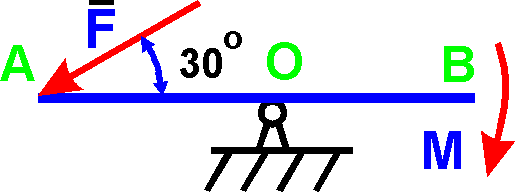 ). 1,5 Н;

Б). 2·1,41Н;

В). 3 Н;

Г). 3·1,73 H.

Література:

1. Мовнин М. С., Израелит А. Б., Рубашкин А. Г. “Основы технической механики”.Л.: Машиностроение, 1979-288с. - .

2. Эрдеди А. А., Медведев Ю. А., Эрдеди Н. А. Техническая механика: Теоретическая механика. Сопротивление материалов. М.: Высш. Шк.,1991.

3. Павловський М.А. «Теоретична механіка» Київ: Техніка, 2002. – 510 с. – Для студентів ВНЗ.

4. Бондаренко А.А. Теоретична механіка. Частина 1. Статика. Кінематика Підручник у 2 ч. – К.: Знання, 2004. – 599 с.

5. Тарг С.М. Краткий курс теоретической механики. - М.: Вьісш. шк., 1986. - 416с