Лекція №2

Тема лекції:

Плоска система збіжних сил

Мета навчальна: формування знань щодо графічних та аналітичних методів визначення сили

Мета виховна: засвоєння нових знань

Мета розвиваюча: Вивчення питань цієї лекції необхідно в подальшому для вивчення центру ваги, довільної просторової системи сил, сил тертя ковзання, моментів тертя кочення, вирішення завдань у дисципліні «Опір матеріалів».

План лекції:

1 Геометричний спосіб визначення рівнодійної системи збіжних сил

2. Умова рівноваги системи збіжних сил (графічна)

3. Проекція сили на вісь

4. Проекція сили на дві взаємно перпендикулярні осі

5. Аналітичний спосіб визначення рівнодійної системи збіжних сил

6. Аналітична умова рівноваги системи збіжних сил (рівняння рівноваги)

Знання, які студент повинен отримати під час лекції:

1. Складання системи сил векторним (графічним) методом;

2. Складання системи сил аналітичним методом;

3. Графічну і аналітичну умови рівноваги системи збіжних сил.

Система сил, лінії яких перетинаються в одній точці і лежать в одній площині, називається плоскою системою збіжних сил (сзс).

1. Геометричний спосіб визначення рівнодійної системи збіжних сил

Правило трикутника

(Для складання двох збіжних сил)

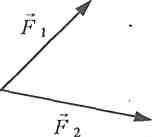а)

Мал. 2.1.

З кінця сили відкладемо силу (зберігаючи напрям та величину). Потім з'єднаємо початок сили з кінцем сили . Це буде рівнодійна цих сил (мал. 2.1, б).

Знайдемо рівнодійну системи сил , , , (мал. 2.2,а).

а)

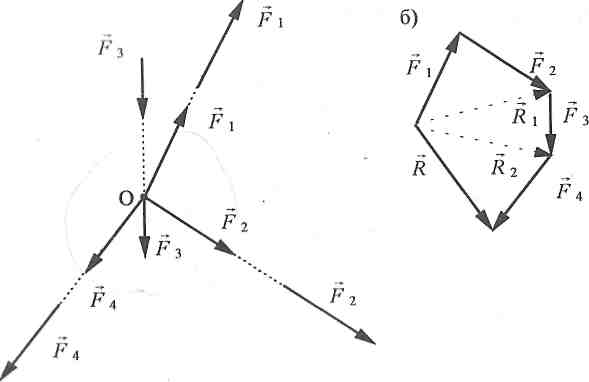
a)

Мал. 2.2.

Перенесемо сили по лініям їх дій у точку О. Дістанемо систему збіжних сил. Додавши сили та , матимемо рівнодійну (мал. 2.2, б);

Потім до додамо силу і дістанемо рівнодійну (мал. 2.2,6);

Нарешті, до рівнодійної ₂ додамо силу ₄ і матимемо загальну рівнодійну

заданої системи:

Отже, для будь-якого числа сил рівнодійна системи збіжних сил дорівнює геометричній сумі заданих сил системи.

Побудований багатокутник називається силовим. Проміжні вектори і можна не будувати.

2. Умова рівноваги системи збіжних сил (графічна)

мал.2.3.

Система збіжних сил буде у стані рівноваги, якщо при побудові силового багатокутника кінець останньої сили системи приходить у початок першої, тобто рівнодійна сила системи дорівнює нулю (мал. 2.3).

3. Проекція сили на вісь

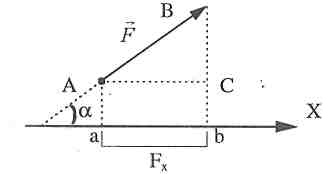
ВІСЬ - це пряма, яка має певний напрям. Проекція сили на вісь - відрізок аЬ, який дорівнює віддалі між основами перпендикулярів опущених з початку і кінця сили на вісь (мал. 2.4). мал. 2.4

Проекція сили - скалярна величина (не має напряму).

З прямокутного трикутника АВС маємо:

cosα=AC/AB=Fx/F

тоді

Проекція сили на вісь дорівнює добуткові величини цієї сили F на косинус кута, який ця сила утворює з віссю проекцій.

Знак проекцій

Частні випадки

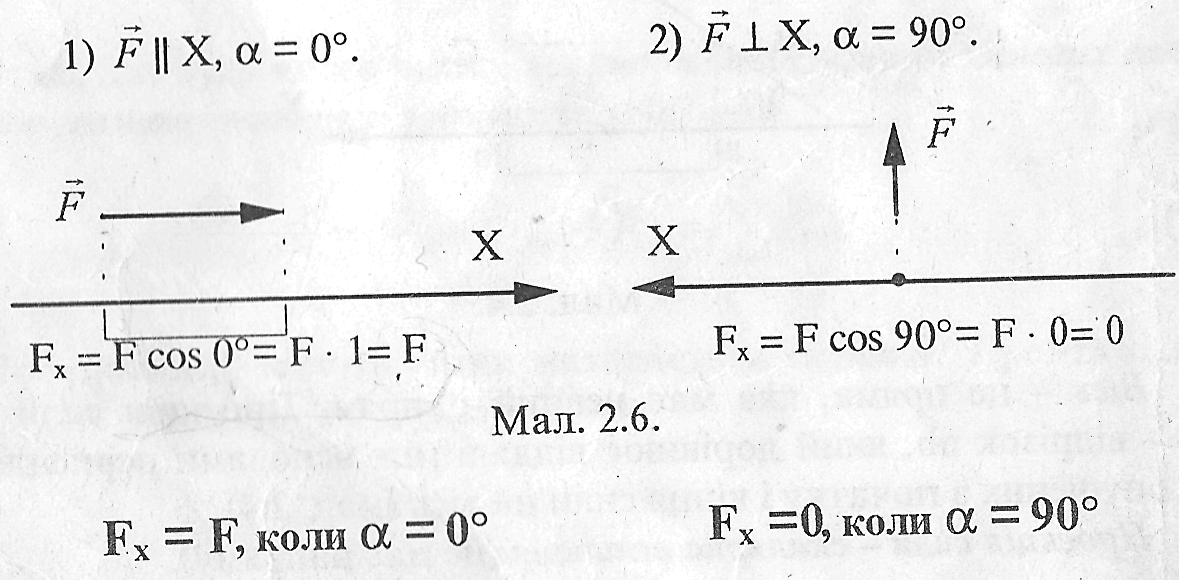
4. Проекція сили на дві взаємно перпендикулярні осі

Мал. 2.7.

Спроектуємо силу на дві взаємно перпендикулярні осі X та У.

З прямокутного трикутника АВС знаходимо

Але АС = Fх; ВС = Fу; АВ = F. Отже,

(2.4)

Це рівняння визначає модуль сили, якщо відомо її проекції на дві взаємно перпендикулярні осі.

Напрям сиди визначають з кутів α та β, які сила утворює з осями.

З трикутника АВС маємо

Положення сили на площі цілком визначається її проекціями на дві взаємно перпендикулярні осі проекцій.