Лекція №6

Тема лекції:

Центр ваги

Мета навчальна: формування знань щодо методів визначення цента ваги складної фігури.

Мета виховна: засвоєння нових знань

Мета розвиваюча: Вивчення питань цієї лекції необхідно в подальшому для, сил тертя ковзання, моментів тертя кочення, вирішення завдань у дисципліні «Опір матеріалів», «Деталі машин і механізмів»

План лекції:

1. Центр паралельних сил.

2. Центр ваги.

3. Координати центра ваги простих геометричних фігур

Знання, які студент повинен отримати під час лекції:

4. Методи визначення координат центра ваги тіл;

5. Координати цента ваги простих геометричних фігур;

1. Центр паралельних сил.

Для системи паралельних сил введемо поняття центра паралельних сил.

На тіло діє система паралельних сил , прикладених у точках . Оберемо осі координат так, щоб вісь Оz була паралельна силам.

, ,

– проекція сили на вісь Oz.

Точка С з координатами називається центром паралельних сил .

– проекція сили на вісь Oz.

Властивості центра паралельних сил:

1. сума моментів усіх сил відносно точки С дорівнює нулю

2. якщо всі сили обернути на один і той самий кут, не міняючи точок прикладення сил, то центр нової системи паралельних сил буде тією самою точкою С.

2. Центр ваги.

Вага тіла-це сила, з якою тіло притягується до центра Землі. Ця сила називається силою тяжіння

Величина рівнодійної системи паралельних сил, що діють на частки тіла є силою тяжіння, яка прикладена в центрі ваги тіла

Центром ваги тіла називається геометрична точка, жорстко пов'язана з цим тілом, що є центром паралельних сил ваги, прикладених до окремих елементарних частинок тіла.

Якщо тіло однорідне, то вага кожної частки тіла пропорційна його об’єму, довжині, площі:

Центр ваги однорідного твердого тіла

де - об’єм елементарної частки тіла;

Центр ваги однорідного стержня

Стержнем називають тіло, один розмір якого (довжина) набагато більше двох інших.

де - довжина елементарної частки стержня;

Центр ваги однорідної пластини

де - площа елементарної частки пластини;

xi, yi –координати центра ваги елементарної частки пластини

Вираз називають статичним моментом площі (Sy.).

Осі, що проходять через центр ваги, називаються центральними осями. Статичний момент щодо центральної осі дорівнює нулю.

3. Координати центра ваги простих геометричних фігур

Положення центрів ваги простих геометричних фігур можуть бути розраховані за формулами

а) - коло, б) - квадрат, прямокутник, в) - трикутник; г) - півколо)

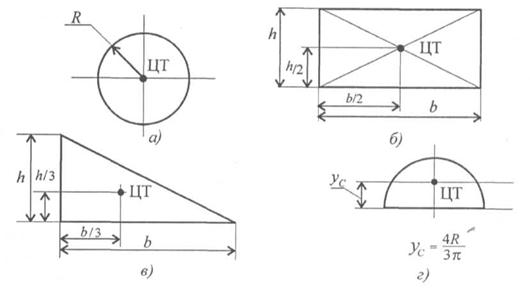
При вирішенні завдань використовуються такі методи:

метод симетрії: центр ваги симетричних фігур знаходиться на осі симетрії;

метод поділу: складні перетини поділяємо на кілька простих частин, положення центрів ваги яких легко визначити;

метод від'ємних площ: порожнини (отвори) розглядаються як частина перетину із від'ємною площею.

Приклад 1.

Визначити координати центра ваги площі фігури (рис. 3.24,а).

а	Розв’язання. Розіб’ємо фігуру на три елементарні фігури, для яких відомі центри ваги, та легко визначаються площі: прямокутник, трикутник і півколо (рис. 3.24,б). Площу півкола, вирізану з прямокутника, вважаємо тілом з від’ємною площиною. Координати центра ваги плоскої фігури визначаємо за формулами ; ,
б Рис. 3.24

де 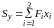, - статичні моменти фігури відносно координатних осей і , - площа фігури.

Дані про площі елементарних фігур (прямокутника, трикутника та півкола), координати їхніх центрів ваги, статичних моментів відносно координатних осей запишемо в таблиці.

1	1200	15,0	20,0	18000	24000
2	1000	46,7	13,3	46700	13300
3	-628	8,5	20,0	-5338	-12500
	1572	‑	‑	59362	24700

Координати центра ваги всієї фігури:

;

.

Центр ваги площі всієї фігури показуємо на рисунку.

Контрольні питання (завдання):

1. що таке сила тяжіння?

2. Яка точка називається центром ваги тіла?

3. За якими формулами визначають центр ваги об’ємної фігури, однорідного тонкого стержня?

4. Як визначають центр простих геометричних фігур?

5. Як визначають центр ваги плоскої фігури?

Література:

6. Мовнин М. С., Израелит А. Б., Рубашкин А. Г. “Основы технической механики”.Л.: Машиностроение, 1979-288с. - .

7. Эрдеди А. А., Медведев Ю. А., Эрдеди Н. А. Техническая механика: Теоретическая механика. Сопротивление материалов. М.: Высш. Шк.,1991.

8. Павловський М.А. «Теоретична механіка» Київ: Техніка, 2002. – 510 с. – Для студентів ВНЗ.

9. Бондаренко А.А. Теоретична механіка. Частина 1. Статика. Кінематика Підручник у 2 ч. – К.: Знання, 2004. – 599 с.

10. Тарг С.М. Краткий курс теоретической механики. - М.: Вьісш. шк., 1986. - 416с