Основы теории вероятности

Введение

Результат (исход) опыта или наблюдения называют событием.

Пусть производится опыт, в результате которого может произойти или не произойти некоторое событие; такие события называют случайными (или возможными) событиями.

В общих словах вероятность – это мера правдоподобия что отдельное событие произойдёт (случиться) в некотором испытании или эксперименте, проводимом при известных условиях. Вероятность – это числовая характеристика шанса, возможности появления случайного события.

Каждый отдельный возможный результат испытания называется исход.

Способность предсказать вероятные события имеет очевидное прикладное значение, например, в страховых случаях и в процессе контроля качества продукции и эффективного использования ресурсов.

Обозначения

Вероятность того, что событие А произойдёт обозначается как P(A).

Например. Если A представляет собой событие, означающее, что деталь, взятая случайным образом из партии, неисправна, можно написать A={бракованная деталь}, то P(A) обозначает вероятность получения бракованной детали (вероятность того, что взятая наугад деталь окажется бракованной).

Отбор образцов

Для полной проверки производимых деталей важны оба аспекта – затраченное время и экономичность изготовления. Время от времени из общей партии произведённых деталей случайным образом отбирают множество (набор) образцов. Чем выше случайность образца, тем точнее образец представляет свою партию – целую популяцию.

Типы вероятности

Существует два подхода к определению вероятности:

а) эмпирическая (или экспериментальная) вероятность;

в) классическая (или теоретическая) вероятность.

Рассмотрим их подробнее.

Эмпирическая вероятность

Эмпирическая вероятность основана на заранее известных результатах. По частоте события можно оценить возможность его появления в будущем. Относительную частоту называют ещё эмпирической вероятностью.

Рассмотрим пример. В результате тщательной проверки случайным образом отобранных 240 деталей найдено 20 бракованных. Таким образом, при случайном выборе одной детали шанс того, что она окажется бракованной составляет 20 из 240 или 1 из 12.

Итак, если

A={бракованная деталь}, то P(A)=1 из 12= =0,0833=8,33%.

Принято писать P(A)= . или P(A)=0,0833.

Аналогичным образом, можно рассчитать, сколько бракованных деталей будет содержаться в партии из 600 деталей, изготовленных на той же машине:

поскольку P(A)= , то в партии из 600 деталей число бракованных x будет вычисляться по формуле: x=600 * =50.

Ожидание

Полученный результат не утверждает, что в любом другом наборе из 600 деталей точно 50 будут дефектными, но имея значение вероятности появления такого события ( ), мы можем рассчитать количество их появлений в наборе из N деталей (общее число испытаний).

Ожидание Е определяется как произведение числа испытаний (N) на вероятность P(A) того, что событие A произойдёт в любом испытании, т.е.

E=N*P(A) (1)

Успех или неудача

(Благоприятный исход или неблагоприятный исход)

До сих пор мы рассматривали вероятности события в частном случае (конкретной задаче). Если событие происходит в любом одном испытании (опыте), то говорят о благоприятном исходе события, в противном случае говорят о неблагоприятном исходе для события – в любом случае событие может быть (произойти).

Если в N испытаниях получилось x благоприятных исходов, значит, число неблагоприятных исходов можно вычислить по формуле (N-x), тогда справедливо равенство

x + ( N-x)=N.

Но =P (успеха)=P(A) и

Таким образом

P(A)+P(not A)=1

Событие not A называется дополнением к событию A и часто обозначается 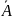, таким образом можно записать

P(A)+P( )=1

Если вероятность выбора бракованной детали составляет , то вероятность не выбора бракованной детали составляет .

Объём (размер) выборки

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали.

Иногда проводят сплошное обследование, т.е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объёмом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объём генеральной совокупности N=1000, а объём выборки n=100.

Объём исходной выборки, по которой было установлено значение вероятности, влияет в целом на достоверность результата. Вероятности, полученные на основании маленьких выборок, редко отражают вероятности, имеющие отношение к целой популяции. Чем больше размер исходной выборки, тем более достоверными получаются результаты.

Например, 15% опрошенных не были склонны к толерантности. Определите количество людей, склонных к толерантности среди 120 опрошенных.

Поскольку 15% отвергают толерантность, то 85% принимают её. Если обозначить событие А={принятие толерантности}, то P(A)=85%= . N=120 и E=N*P(A)=120* =102. Следовательно, ожидаемое число людей, принимающих толерантность, составляет 102.

Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной).

В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.