Задача 6

Средствами векторной алгебры найти:

1) объем пирамиды с вершинами ;

2) длину ребра ;

3) площадь грани ;

4) угол между ребрами и .

Даны координаты вершины пирамиды (5, 1, -4); (1, 2, -1);

(3, 3, -4); (2, 2, 2).

Решение. Построим схематически данную пирамиду (рис.1).

Рис. 1

1. Рассмотрим векторы , и . Зная координаты точек, вычислим координаты этих векторов:

Объем пирамиды равен модулю одной шестой доли смешанного произведения векторов , , .

2. Найдем длину ребра :

3. Вычислим площадь грани .

Площадь равна половине площади параллелограмма, построенного на векторах и . Площадь параллелограмма, построенного на векторах и , совпадает с модулем векторного произведения , а поэтому площадь

4. Найдем угол между ребрами и . Угол между векторами и вычислим по формуле:

По таблицам .

Задача 7

Даны две системы векторов:

1) ;

2) .

Определить, какая из этих систем образует базис; разложить вектор по этому базису.

Решение. Используем признак линейной независимости для векторов с числовыми координатами. Найдем определитель:

, следовательно, система векторов линейно независима и образует базис.

Вычислим определитель для второй системы:

Система линейно зависима.

Проведем разложение вектора по базису . Запишем разложение вектора в координатной форме:

Получаем систему линейных уравнений:

Систему можно решать любым методом. Решим методом последовательного исключения неизвестных:

Итак, координаты вектора в новом базисе будут , а разложение вектора по базису имеет вид .

Задача 8 Привести к каноническому виду уравнение кривой второго порядка

и построить эту кривую.

Решение. Запишем матрицу квадратичной формы

.

Используем собственные нормированные ортогональные векторы:

и

для построения матрицы преобразования :

.

Чтобы сохранить взаимную ориентацию новых координатных осей, на матрицу налагают дополнительное условие (если , то достаточно поменять столбцы местами и сменить соответственно нумерацию у характеристических чисел и собственных векторов).

Квадратичная форма в новой системе координат имеет вид:

.

Преобразуем линейную функцию данного уравнения

В системе координат уравнение кривой имеет вид:

Совершаем параллельный перенос:

В результате уравнение кривой принимает вид: Это уравнение эллипса. В системе координат строим векторы и и определяем направление осей координат . Центр эллипса в системе в точке (рис.2).

Рис. 2

Задача 9.

Три отрасли промышленности I, II и III являются производителями и в тоже время потребителями некоторой продукции. Их взаимосвязь определяет матрица А коэффициентов прямых затрат:

Известен вектор Y объемов конечной продукции:

,

то есть конечный продукт, полученный первой производящей отраслью y₁ = 1000 ед., второй – y₂ = 800 ед., третьей – y₃ = 700 ед.

1. Составим уравнение межотраслевого баланса. Для этого введем вектор валового продукта:

где х₁ – объем валовой продукции I отрасли

х₂ – объем валовой продукции II отрасли

х₃ – объем валовой продукции III отрасли

Уравнение межотраслевого баланса в матричном виде имеет вид:

Х = АХ + Y (*)

Записав его с учетом исходных условий задачи, в виде системы алгебраических уравнений получим:

(1)

2. Для удобства решения системы (1) вначале запишем ее в общем виде:

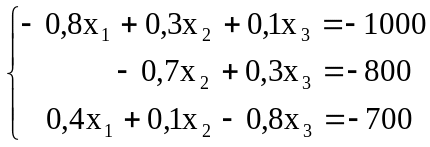
Решение проведем методом последовательного исключения неизвестных (методом Гаусса) с точностью до двух знаков после запятой.

Из последней системы получим:

х₃  2311,11

х₂  4800 + 3 2311,11 = 2133,33

х₁  - 1750 + 2 2311,11 – 0,25  2133,33 = 2338,89

Таким образом объем валовой продукции каждой из трех производящих отраслей в стоимостном выражении:

х₁  2338,89 ед.

х₂  2133,33 ед.

х₃  2311,11 ед.

3. Составим матрицу Х потоков средств производства, зная что х _ij = а _ij х _j, (i,j=1,2,3)

x₁₁ = 0,22338,89 = 467,78

x₁₂ = 0,32133,33 = 640

x₁₃ = 0,12311,11 = 231,11

x₂₁ = 0  2338,89 = 0

x₂₂ = 0,32133,33 = 640

x₂₃ = 0,32311,11 = 693,33

x₃₁ = 0,42338,89 = 935,56

x₃₂ = 0,12133,33 = 213,33

x₃₃ = 0,22311,11 = 462,22

Матрица

4. Вычислим общие доходы каждой потребляющей отрасли

P₁ = 2338,89  (467,78 + 935,56) = 935,55

P₂ = 2133,33  (640 + 640 + 213,33) = 640

P₃ = 2311,11  (231,11 + 693,33 + 462,22) = 924,45

5. Составим таблицу межотраслевого баланса

Потребляющие отрасли Производящие отрасли	I	II	III	Конечный продукт	Валовой продукт
I	467,78	640	231,11	1000	2338,89
II	0	640	693,33	800	2133,33
III	935,56	213,33	462,22	700	2311,11
Общий доход	935,55	640	924,45
Валовой продукт	2338,89	2133,33	2311,11

6. Матричное уравнение () легко приводится к виду (E  A)X = Y, откуда следует уравнение X = (E  A)^-1Y, дающее иную возможность вычислить вектор валового продукта. Матрица Аn = (E  A)^-1 называется матрицей коэффициентов полных затрат.

Для вычисления матрицы Аn вначале находится матрица:

Определитель этой матрицы:

det (E-A) = 0,80,70,80,30,30,40,40,70.10,10,30,8 = 0,36  0

Затем вычисляются алгебраические дополнения А_ij матрицы (EA)

= 0,25

По правилу вычисления обратной матрицы находим:

Литература

1. Гусак А.А. Высшая математика. - Минск, 2001. – Т. 1-2.

2. Красс М.С. Математика для экономических специальностей. - М., 2007.

3. Кремер П.Ш. Высшая математика для экономистов. - М., 2007.

4. Самарина Ю.П., Сахабиева Г.А., Сахабиев В.А. Высшая математика: учебное пособие. – М.: Машиностроение, 2006.

5. Щипачев В.С. Высшая математика. - М., 2007.

6. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М., 2005.

7. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие.- 3-е изд.- М.: Дело, 2004.- 440 с.

8. Просветов Г.И. Математические методы в экономике: Учебно-метод. пособие.- М.: РДЛ, 2004.

42