Rational numbers

Why did the math book look so sad?

Because it had so many problems!

Task 1

Solve the problems:

1. I am a number. If you multiply the number of minutes in a day by the number of hours in a week, you will find half my value.

2. I am a product. I have two factors. One of my factors is the last year of the twentieth century. My other factor is half of a pair. What am I?

3. If you take 3 eggs out of 5, how many will you have?

Task 2

Get ready for module text reading. Practice active vocabulary on the topic:

1) Read the words in the left column paying attention to their pronunciation.

2) Find the Ukrainian equivalents in the right column. Spare column is left for your notes.

calculus measurement rational number irrational natural whole integer square number (perfect square) fraction square root mathematician to accept existence to prove to disprove numerator denominator a set ratio sequence to enumerate

Множина Чисельник Довести Знаменник Спростувати Відношення, коефіцієнт Ряд, послідовність Існування Обчислення Математик Приймати Квадратний корінь Дріб Квадрат цілого числа Ціле число Натуральне число Раціональне число Вимірювання Ірраціональне число Перераховувати Ціле число (+/ –)

Task 3

Translate into Ukrainian:

A theory of measurement, simple and decimal fractions, square root of 9, a set of rationals, sequence of natural numbers, to prove existence of irrational numbers, using geometry, to accept a new theory, to enumerate whole numbers and their algebraic negatives, ratio of x to y, to form a field, a numerator less than denominator, denominator equal or greater than 1, let us start, a double sign, can be written, could be represented, can disprove, could express, it derived from, real line, a simple fraction.

Task 4

Translate into English:

Довести теорему, спростувати існування ірраціональних чисел, система вимірювання, множина натуральних чисел, квадрат цілого числа, простий дріб, математик стародавньої Греції, знаменник та числівник, утворювати поле, послідовність раціональних чисел, квадратний корінь 2, числова пряма, вперше з’явитися в роботі, перерахувати всі можливі варіанти, як їх називають, давайте почнемо з самого початку, набагато більше таких чисел.

Task 5

Read the text and say if the square root of 2 is a rational or irrational number.

Rational and irrational numbers

Calculus is a theory of measurement. The necessary for measuring numbers are the rationals and irrationals. But let us start at the beginning.

The following numbers of arithmetic are the counting-numbers or, as they are called, the natural numbers: 1,  2,  3,  4,  and so on. If we include 0, we have the whole numbers: 0,  1,  2,  3,  and so on. And if we include their algebraic negatives, we have the integers: 0,  ±1,  ±2,  ±3,  and so on. ± ("plus or minus") is called the double sign.

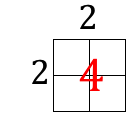
The following are the square numbers, or the perfect squares: 1   4   9   16   25   36   49   64, and so on. They are the numbers 1· 1,  2· 2,  3· 3,  4· 4,  and so on. Square numbers are the product of a number multiplied by itself. An exponent (the small number after the base number) shows how many times to multiply a number by itself: 5² means multiply 5 x 5; 5³ means multiply 5 x 5 x 5. Square numbers can be graphed as a rectangular array with equal sides, or in other words, a square. For example:

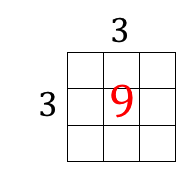
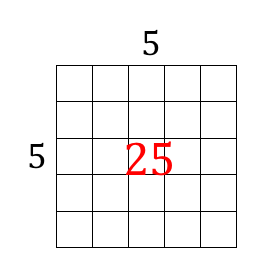
2 x 2 = 4	3 x 3 = 9	5 x 5 = 25

A rational number is a number that can be written as a simple fraction ( or as a ratio in other words). Example 1.5 is a rational number because 1.5 = 3/2 (it can be written as a fraction).

Here are some more examples:

Number	As a Fraction	Rational?
5	5/1	Yes
1.75	7/4	Yes
.001	1/1000	Yes
0.111...	1/9	Yes
√2  (square root of 2)	?	NO !

5 can be represented as a ratio or a quotient of 5 and 1 and so on. But the square root of 2 cannot be written as a simple fraction. And there are many more such numbers, and because they are not rational they are called irrational.

The ancient Greek mathematician Pythagoras believed that all numbers were rational in other words could be written as a fraction, but one of his students Hippasus proved (using geometry, it is thought) that you could not represent the square root of 2 as a fraction, and so it was irrational.

However Pythagoras could not accept the existence of irrational numbers, because he believed that all numbers had perfect squares. But he could not disprove Hippasus' "irrational numbers" and so Hippasus was thrown overboard and drowned!

But nowadays we know that a rational number is a number that can be expressed as a fraction p/q where p and q are integers and  q is not equal to 0. A rational number p/q is said to have numerator p and denominator q. Numbers that are not rational are called irrational numbers. The real line consists of the sets of the rational and irrational numbers.

The set of all rational numbers is referred to as the "rationals," and forms a field that is denoted   . Here, the symbol   derives from the word Quotient, which means "the result of division", "ratio," and first appeared in Nicolas Bourbaki's "Algebra".

Examples of rational numbers include  , 0, 1, 1/2, 22/7, 12345/67, and so on. Farey sequences provide a way of enumerating all rational numbers systematically.

Task 6

Answer the questions on the text.

1. What is calculus?

2. What do we need to measure numbers?

3. What is a natural number? Give examples.

4. What do the natural numbers include?

5. What do the integers include?

6. How can the perfect squares be presented?

7. How can a rational number be written? Give examples.

8. Did ancient Greeks know about irrational numbers?

9. How can a rational number be expressed?

10. What does any fraction consist of?

11. Why is the set of rationals often denoted as a field Q?

12. What is Farey sequence?

Task 7

Fill in the gaps: