Тема 8. Статистичні методи вимірювання взаємозв’язків

Усі соціально-економічні явища взаємопозв’язані та взаємозумовлені і залежність між ними має причинно-наслідковий характер. Ознака, що є причиною зв’язку, називається факторною x, а та, що змінюється під впливом факторної ознаки – результативним y.

Між ознаками x та y існують різні типи зв’язків.

При функціональному зв’язку між факторною та результативною ознаками кожному значенню ознаки x відповідає одне чітко визначене значення ознаки y. Такі зв’язки найчастіше вивчаються в математичному аналізі. Наприклад, значенню відповідає тільки одне значення .

При стохастичному зв’язку кожному окремому значенню факторної ознаки x відповідає певна множина значень результативної ознаки y.

Підвидом стохастичного зв’язку є кореляційна залежність, коли середня величина результативної ознаки змінюється залежно від факторної ознаки x (табл. 8.1).

Таблиця 8.1 – Кореляційна таблиця

Ознаки	y1	y2	y3	…	yn
x1
x2
x3
…
xn

Кореляційний зв’язок між ознаками x і y записується в аналітичному вигляді  рівняння регресії.

Вивчення кореляційного зв’язку між ознаками починається з регресійного аналізу, який вирішує проблему встановлення форми зв’язку, або виду рівняння регресії, та визначення параметрів рівняння регресії.

У регресійному аналізі розрізняють рівняння парної та множинної регресії. Коли результативна ознака залежить від одної факторної ознаки, то рівняння регресії має назву рівняння парної регресії, якщо результативна ознака y пов’язана з декількома видами факторних ознак x_i, то така залежність має назву рівняння множинної регресії.

Найчастіше використовують такі рівняння:

а) лінійне (рис. 8.1);

б) параболічне (рис. 8.2);

в) гіперболічне (рис. 8.3);

г) степеневе (рис. 8.4),

де  параметри, які знаходяться методом найменших квадратів.

Y

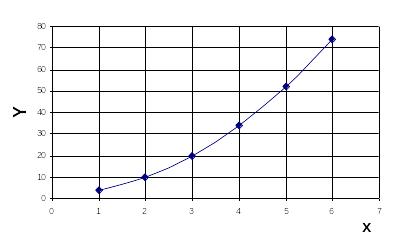
Рисунок 8.1 – Лінійна залежність Рисунок 8.2 – Параболічна залежність

Рисунок 8.3 – Гіперболічна залежність Рисунок 8.4 – Степенева залежність

У випадку лінійного виду параметри регресії розраховуються використовуючи метод найменших квадратів за такими формулами:

, , (8.1)

Для оцінки впливу факторної ознаки на результативну розраховується коефіцієнт еластичності в середньому для усієї сукупності:

, (8.2)

де ,  середні величини фактичних даних відповідно за факторною та результативною ознаками в цілому для сукупності.

Коефіцієнт еластичності показує, на скільки процентів у середньому зміниться результативна ознака при зміні факторної ознаки на 1 %.

У разі використання параболічного виду рівняння регресії параметри регресії розраховуються за наведеними формулами, в яких необхідно замість ознаки x підставити :

, . (8.3)

При гіперболічному виді під час розрахунку параметрів регресії під ознакою слід розуміти .

У випадку використання рівняння регресії степеневого виду , ; ; :

; . (8.4)

Після розрахунку параметру із співвідношення визначається значення з використанням таблиць логарифмів.

(8.5)

Для вибору виду рівняння регресії необхідно побудувати графік залежності фактичних даних і за групуванням точок на графіку встановити візуально, до якого виду можна віднести лінію регресії.

Після вибору рівняння регресії та знаходження його параметрів розпочинають другий етап аналізу, в межах якого дають оцінку тісноти та значимості зв’язку.

У поняття «тіснота зв’язку» вкладається оцінка впливу факторної ознаки на результативну та встановлення адекватності теоретичної залежності між ознаками фактичним даним. Тісноту зв’язку між ознаками оцінюють за допомогою коефіцієнту детермінації та коефіцієнту кореляції.

Коефіцієнт детермінації показує, на скільки обрана аналітична залежність (регресія) адекватна первинним статистичним даним, тобто на скільки вона пояснює зміну результативної ознаки під впливом фактору.

, (8.6)

де  значення результативної ознаки , що розраховано за рівнянням регресії;

 значення результативної ознаки за статистичними даними.

Коефіцієнт детермінації набуває значення від 0 до 1. Чим ближче до 1, тим «краще» регресія. Якщо = 0, то рівняння регресії не пояснює, чому змінюється результативна ознака, тобто вона не адекватна статистичним даним.

Коефіцієнт кореляції визначається за формулою і показує ступінь тісноти лінійної залежності між x та y:

(8.7)

Він може набувати будь-яких значеннь від -1 до 1. Чим ближче коефіцієнт кореляції за абсолютною величиною до 1, тим більш тісний зв'язок між ознаками. Знак при коефіцієнті кореляції вказує на напрямок зв’язку. Пряма залежність відповідає знаку «+», зворотній зв'язок – знаку «-».

Після встановлення тісноти зв’язку дають оцінку значимості зв’язку між ознаками. Під терміном «значимість зв’язку» розуміють оцінку відхилення вибіркових змінних від своїх значень у генеральній сукупності за допомогою статистичних критеріїв – F- критерію Фішера і t-критерія Ст’юдента.

Для парної регресії перевіряємо нульову гіпотезу, яка полягає в тому, що у генеральній сукупності коефіцієнт детермінації дорівнює нулю

F- критерій Фішера: .

Значення критерію порівнюють з табличним (критичним) залежно від ступенів вільності та прийнятого рівня значимості, тобто імовірності помилитися та приймати невірну гіпотезу. ,  рівень значимості. ,  довірча імовірність, тобто імовірність, що буде прийнята вірна гіпотеза (додаток Б).

Якщо , то відхиляємо гіпотезу , тобто з імовірністю можна стверджувати, що в генеральній сукупності коефіцієнт детермінації не дорівнює нулю.

Перевіримо, чи буде в генеральній сукупності коефіцієнт кореляції дорівнювати нулю.

t-критерій Ст’юдента .

Значення критерію порівнюють з табличним (критичним) залежно від ступенів вільності та прийнятої довірчої імовірності. (додаток А). Якщо , то відхиляємо гіпотезу , тобто з імовірністю можна стверджувати, що в генеральній сукупності коефіцієнт кореляції не дорівнює нулю, тобто коефіцієнт кореляції визначається значимим при характеристиці генеральної сукупності.

Приклад. За даними статистичних спостережень необхідно:

1. розрахувати параметри лінійного рівняння парної регресії, що характеризує залежність між тижневим роздрібним товарооборотом (грн) на душу населення та доходами населення (грн), та зробити аналіз параметрів регресії за даними (табл. 8.2);

2. оцінити тісноту та значимість зв’язку між ознаками.

Таблиця 8.2 – Статистичні дані

Доходи населення	18	20	21	22	24	25	27	28	29	31
Роздрібний товарооборот	17	18	19	20	21	23	24	25	26	27

1. У даній задачі факторною ознакою (х) будуть тижневі доходи населення на одну особу за відповідними групами, а результативною ознакою (y) – роздрібний товарооборот.

Для обґрунтування виду рівняння регресії зобразимо статистичні дані графічно (рис. 8.5)

Рисунок 8.5 – Графічне зображення статистичних даних

Очевидно, в якості теоретичної залежності y від х доцільно використовувати лінійне рівняння парної регресії: . Розрахуємо значення параметрів .

Розрахунки представимо у вигляді таблиці 8.3.

Таблиця 8.3 – Розрахункові дані

№	х	y	x2	xy	Y
1	18	17	324	306	16,68
2	20	18	400	360	18,32
3	21	19	441	399	19,14
4	22	20	484	440	19,96
5	24	21	576	504	21,59
6	25	23	625	575	22,41
7	27	24	729	648	24,05
8	28	25	784	700	24,87
9	29	26	841	754	25,69
10	31	27	961	837	27,32
Усього	245	220	6165	5523
У середньому	24,5	22,0	616,5	552,3

;

.

Або ; .

Отже, теоретична залежність роздрібного товарообороту від доходів населення має вигляд:

.

Коефіцієнт еластичності: .

Зі збільшенням доходів населення на 1 % роздрібний товарооборот зростає на 0,91 %.

2. Допоміжні розрахунки для визначення характеристик тісноти та значимості зв’язку зручно подавати у табличній формі (табл. 8.4):

Дамо оцінку адекватності рівняння регресії статистичним даним, розрахувавши коефіцієнт детермінації:

.

Таблиця 8.4 – Розрахункові дані

Значення коефіцієнту детермінації свідчить про те, що зв'язок між ознаками тісний, та рівняння регресії добре відповідає первинним даним і пояснює, чому змінюється результативна ознака, тобто варіація роздрібного товарообороту на 98,97 % визначається варіацією доходів населення, а на 1,03 %  впливом неврахованих у регресійній моделі факторів.

Коефіцієнт кореляції:

Коефіцієнт кореляції свідчить про те, що по-перше, товарооборот має прямо пропорційну тісну залежність від доходів населення.

Оцінимо значимість зв’язку, тобто визначимо чи дійсно існує залежність між ознаками в генеральній сукупності.

Перевіряємо нульову гіпотезу, яка полягає в тому, що у генеральній сукупності коефіцієнт детермінації дорівнює нулю:

F- критерій Фішера: ,

(додаток Б).

Оскільки , то відхиляємо гіпотезу , тобто з імовірністю 0,95 можна стверджувати, що в генеральній сукупності коефіцієнт детермінації не дорівнює нулю.

Перевіримо, чи буде в генеральній сукупності коефіцієнт кореляції дорівнювати нулю.

t-критерій Ст’юдента .

(додаток А), оскільки , то відхиляємо гіпотезу , тобто з імовірністю 0,95 можна стверджувати, що в генеральній сукупності коефіцієнт кореляції не дорівнює нулю, тобто коефіцієнт кореляції визначається значимим при характеристиці генеральної сукупності.