
- •Введение
- •Тема 1 Закон Кулона Напряженность электрического поля
- •Напряженность электрического поля определяется формулой
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Разделим почленно уравнение (1) на (2), получаем уравнение
- •Задача 6
- •Задача 7
- •Задача 8
- •Тема 2 Потенциал
- •Шаровой конденсатор
- •Плоский конденсатор
- •Цилиндрический конденсатор
- •Задача 9
- •Задача 10
- •Работа внешних сил над электроном – работа сил поля равна
- •Задача 11
- •Задача 12
- •Задача 13
- •Задача 14
- •Задача 15
- •Задача 16
- •Задача 17
- •Задача 18
- •Задача 19
- •Задача 20
- •Тема 3 Электроемкость
- •Сила притяжения между пластинами плоского конденсатора
- •Задача 21
- •Задача 22
- •Задача 23
- •Задача 24
- •Задача 25
- •Задача 26
- •Задача 27
- •Задача 28
- •Тема 4 Электрический ток. Закон Ома
- •Задача 29
- •Задача 30
- •Задача 31
- •Задача 32
- •Задача 33
- •Задача 34
- •Задача 35
- •Задача 36
- •Задача 37
- •Задача 38
- •Задача 39
- •Задача 40
- •Задача 41
- •Задача 42
Задача 15
В плоском горизонтально расположенном конденсаторе, расстояние между пластинами которого d=1 см, находится заряженная капелька массой m=510-11 г. При отсутствии электрического поля капелька вследствие сопротивления воздуха падает с некоторой постоянной скоростью. Если к пластинам конденсатора приложить разность потенциалов U=600 В, то капелька падает вдвое медленнее. Найти заряд капельки.
Дано: d = 0,01 м m = 510-14 кг U = 600 В 1 = 22 g = 9,8 м/с |
Решение:
Рассмотрим
процесс падения капли в воздухе. На
капельку действуют две силы: сила
тяжести
При движении капли с постоянной скоростью сумма проекций на вертикальное и горизон- |
q – ? |
тальное направление равна нулю, т. к. а=0. |
 y
y

![]()
![]()
![]()
![]()
Найдем проекции векторов сил на ось Оу:
![]()
Fсопр=mg. (1)
Используя формулу Стокса, выразим Fсопр:
![]() (2)
(2)
Подставив (2) в (1), получаем
![]() (3)
(3)
+qn y
-qn
y
-qn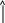
![]()
 U
q
U
q
![]() d
d
На
капельку действуют три силы: сила тяжести
,
сила сопротивления
![]() и сила электрического взаимодействия
и сила электрического взаимодействия
![]() При движении капли с постоянной скоростью
сумма проекций на вертикальное и
горизонтальное направления равны нулю,
т. к. а=0.
При движении капли с постоянной скоростью
сумма проекций на вертикальное и
горизонтальное направления равны нулю,
т. к. а=0.
![]()
Спроецируем векторы сил на ось Оу:
![]()
Fсопр=mg–Fэл. (4)
Используя формулу Стокса, выразим Fсопр
![]()
По определению
Fэл=Eq.
Подставим полученные формулы в (4), получаем
![]() (5)
(5)
Почленно разделив уравнения (3) и (5), получаем
![]()
Отсюда выражаем заряд капли
![]()
Внутри конденсатора имеется однородное электрическое поле с напряженностью
![]()
Тогда
![]()
Вычисления:
![]()
Ответ: заряд капельки q=4,110-18 Кл.
Задача 16
Между двумя вертикальными пластинами на одинаковом расстоянии от них падает пылинка. Вследствие сопротивления воздуха скорость падения пылинки постоянна и равна v=2 см/с. Через какое время после подачи на пластины разности потенциалов U=3 кВ пылинка достигнет одной из пластин? Какое расстояние l по вертикали пылинка пролетит до попадания на пластину? Расстояние между пластинами d=2 см, масса пылинки m=210-9 г, ее заряд q=6,510-17 Кл.
Дано:
|
Решение: а) В отсутствии электрического поля на пылинку действуют две силы: сила тяжести и сила сопротивления . При движении капли с постоянной скоростью сумма проекций на вертикальное и горизонтальное направления равна нулю, т. к. а=0. |
t – ? l – ? |
|
у
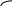
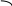 d/2
d/2
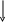
![]()
![]()
Fсопр=mg. (1)
Используя формулу Стокса, выразим Fсопр:
(2)
Подставив (2) в (1), получаем
(3)
d/2 +
x
l у

 q
-q
q
-q
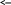
![]() (4)
(4)
Разделим почленно выражения (4) и (3), получаем
![]() (5)
(5)
Напряженность электрического поля в плоском конденсаторе
(6)
Подставляя (5) в (4) получаем
![]()
Пылинка
пролетает расстояние
![]() за время t
со скоростью v2,
т. е.
за время t
со скоростью v2,
т. е.
![]()
Отсюда найдем время t
![]()
Расстояние l пылинка пролетит со скоростью v1 за время t, т. е.
L = v1t.
Вычисления:
![]()
l=210-21 = 2(см).
Ответ: через 1 с после подачи на пластины разности потенциалов U=3000 В пылинка достигнет одной из пластин. За это время она пролетит по вертикали 2 см.

