Задача 5

На рисунке АА — заряженная плоскость с поверхностной плотностью заряда 40 мкКл/м² и В — одноименно заряженный шарик с массой 1г и зарядом 1нКл. Какой угол с плоскостью АА образует нить, на которой висит шарик?

Дано:	Решение: На шарик действуют три силы: сила упругости , сила тяжести и сила кулоновского отталкивания . При равновесии шарика суммы проекций сил на горизонтальное и верти-
 – ?	кальное направления равны нулю.

А 

 

x

В

y

А

Найдем проекции векторов на оси координат

Ох: F_K–F_упрsin=0

Oy: –F_упрcos+mg=0.

F_K = F_упрsin. (1)

mg = F_упрcos. (2)

Разделим почленно уравнение (1) на (2), получаем уравнение

(3)

По определению

F_K=qE. (4)

Напряженность бесконечной плоскости

(5)

Подставим (5) в (4)

(6)

Подставляя (6) в (3), получаем

Вычисления:

Ответ: угол, который образует нить с плоскостью, равен .

Задача 6

С какой силой F_l на единицу длины отталкиваются две одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда 3 мкКл/м, находящиеся на расстоянии r₁=2 см друг от друга? Какую работу на единицу длины надо совершить, чтобы сдвинуть эти нити до расстояния r₂=1 см.?

Дано:	Решение: Напряженность поля, образованного заряженной бесконечно длинной нитью равна (1) а) Сила, действующая
Fl – ?, Аl – ?	на элементарный заряд dq, равна

dF=Edq (2)

Линейная плотность заряда равна

(3)

где dl – длина физически бесконечно малого отрезка нити,

dq – заряд, сосредоточенный на этом отрезке.

dl

dq dF x

r₁

Силу взаимодействия двух нитей можно найти по формуле с использованием формул (1), (2), (3)

где l – длина нити.

Отношение будет равно силе, с которой отталкиваются две нити на единицу длины

(1)

Вычисления:

б) Сила, действующая на отрезок нити равный dl равна

(4)

где х – расстояние между нитями.

Совершаемая при этом работа равна

dA_l=F_ldx. (5)

Интегрируем выражение (5)

(6)

Подставляя в (6) формулу (1) при этом заменяя в (1) постоянный параметр r₁ на изменяющийся параметр х, получаем

Вычисления:

Ответ: две одноименные заряженные бесконечно длинные нити отталкиваются с силой F_l=8,1 Н/м, приходящейся на единицу их длины; чтобы сдвинуть эти две нити на 1 см, надо совершить работу A_l=0,112 Дж/м, приходящуюся на единицу их длины.

Задача 7

В плоском горизонтально расположенном конденсаторе заряженная капелька ртути находится в равновесии при напряженности электрического поля Е=60кВ/м. Заряд капли q= . Найти радиус R капли.

Дано:	Решение: На шарик (каплю) действуют две силы: сила тяжести и сила электростатического взаимодействия. При равновесии капли сумма проекций сил на вертикальное и горизонтальное направления равна нулю.
R – ?	(1)

-

+ у

Найдем проекции векторов сил на ось Оу

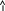
Оу: mg–F_эл=0  mg=F_эл (2)

По определению

В области между плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

По определению

(3)

Подставим формулу (3) в (2), получаем

Вычисления:

Ответ: радиус капли должен быть