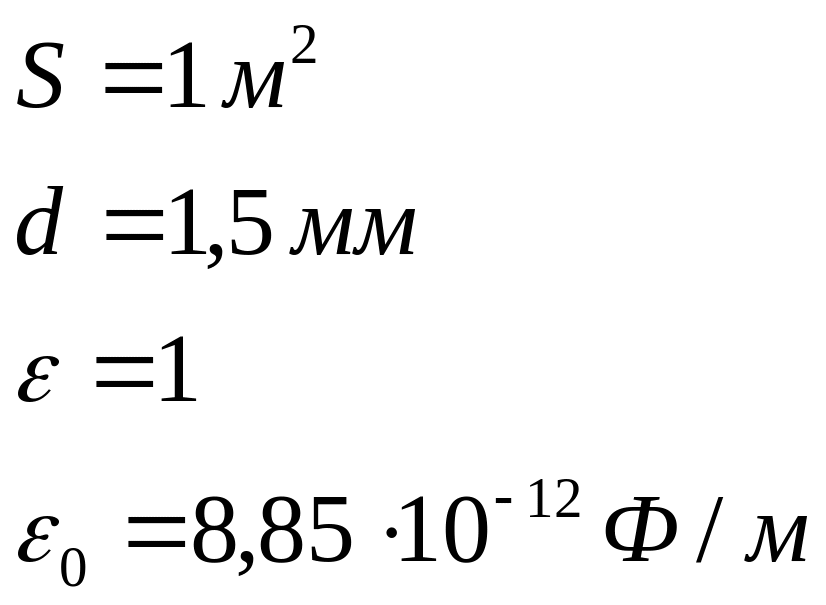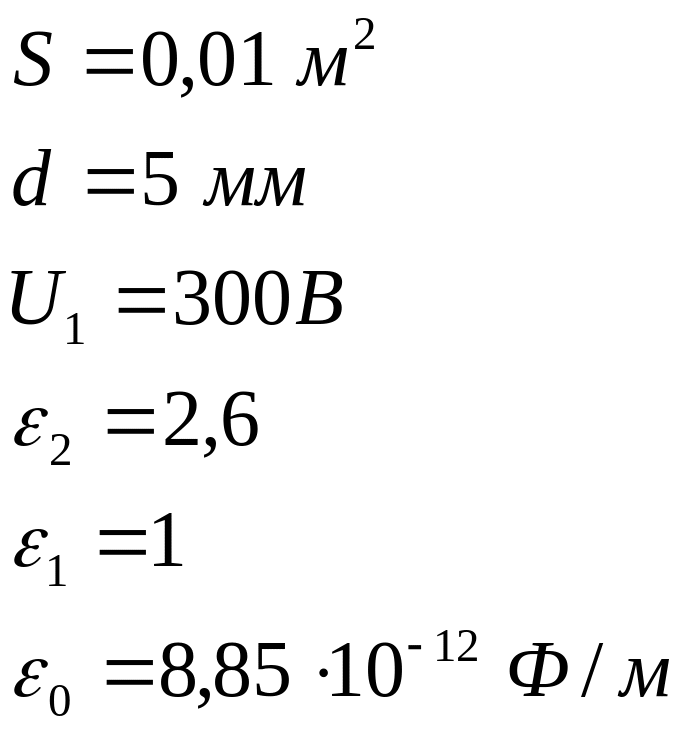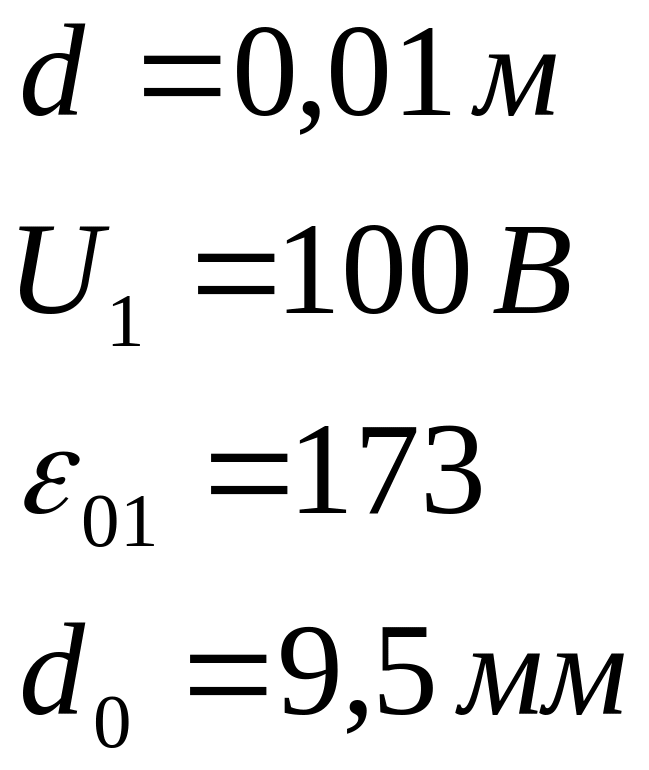Сила притяжения между пластинами плоского конденсатора

Задача 21

Площадь пластин плоского воздушного конденсатора S=1м², расстояние между ними Найти емкость С этого конденсатора.

Дано:	Решение: Если на единице поверхности обкладок имеется заряд  и диэлектриком является вакуум, то полное напряжение между обкладками равно
С – ?	где d – расстояние между пластинами.

d

S

-q +q

Если площадь каждой пластины равна S, то полный заряд пластины есть

поэтому

Вычисления:

Ответ: емкость плоского воздушного конденсатора равна С=5,9 нФ.

Задача 22

Конденсатор предыдущей задачи заряжен до разности потенциалов U=300В. Найти поверхностную плотность заряда на его пластинах.

Дано:	Решение: Вычислим разность потенциалов между положительно заряженной пластиной и произвольной точкой, удаленной на расстояние х от нее. Напряженность поля в плоском конденсаторе выражается формулой
– ?

d

S

-q +q

Поэтому

Полная разность потенциалов U₀ между электродами равна

Вычисления:

Ответ: поверхностная плотность заряда на пластинах конденсатора

Задача 23

Площадь пластин плоского воздушного конденсатора , расстояние между ними d=5 мм. К пластинам конденсатора приложена разность потенциалов . После отключения конденсатора от источника напряжения пространство между пластинами конденсатора заполняется эбонитом. Какова будет разность потенциалов между пластинами после заполнения? Найти емкости конденсатора и поверхностные плотности заряда на пластинах до и после заполнения.

Дано:	Решение: В данном случае q1=q2, где q1 и q2 – заряды на пластинах конденсатора до и после заполнения эбонитом. Таким образом, q=const. Следовательно, и поверхностная плотность заряда на пластинах

d

=1

S

-q +q

d

=2,6

S

-q +q

Так как

то до и после заполнения имеем

Учитывая, что =const и d=const, получим

откуда

До и после заполнения эбонитом имеем

Поверхностная плотность заряда

Вычисления:

Ответ: до и после заполнения эбонитом имеем

Задача 24

Между пластинами плоского конденсатора, находящимися на расстоянии d=1 см друг от друга, приложена разность потенциалов U=100 В. К одной из пластин прилегает плоскопараллельная пластинка кристаллического бромистого таллия ( ) толщиной . После отключения конденсатора от источника напряжения пластинку кристалла вынимают. Какова будет после этого разность потенциалов между пластинами конденсатора?

Дано:	Решение: Конденсатор, находящийся в положении 1, можно представить как батарею из двух последовательно соединенных конденсаторов с различной средой между обкладками. В этом случае одинаков для всех конденсато-
U2 – ?	ров заряд q, равный полному заряду батареи, и мы

можем написать

Напряжение батареи будет равно сумме напряжений на отдельных конденсаторах, т.е.

Следовательно,

Поэтому для емкости С всей батареи находим

d

С

-q +q

d₀

 ₀₁

U₁

С 

d

+q -q

=1

U₂

т. е.

(1)

Пусть С – емкость конденсатора после вынимания пластины.

По определению

(2)

Подставим (1) в (2), получаем

Емкость конденсатора во втором положении

По закону сохранения заряда q=q, т. е.

Вычисления:

Ответ: разность потенциалов станет 1,8 кВ.