
- •Введение
- •Тема 1 Закон Кулона Напряженность электрического поля
- •Напряженность электрического поля определяется формулой
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Разделим почленно уравнение (1) на (2), получаем уравнение
- •Задача 6
- •Задача 7
- •Задача 8
- •Тема 2 Потенциал
- •Шаровой конденсатор
- •Плоский конденсатор
- •Цилиндрический конденсатор
- •Задача 9
- •Задача 10
- •Работа внешних сил над электроном – работа сил поля равна
- •Задача 11
- •Задача 12
- •Задача 13
- •Задача 14
- •Задача 15
- •Задача 16
- •Задача 17
- •Задача 18
- •Задача 19
- •Задача 20
- •Тема 3 Электроемкость
- •Сила притяжения между пластинами плоского конденсатора
- •Задача 21
- •Задача 22
- •Задача 23
- •Задача 24
- •Задача 25
- •Задача 26
- •Задача 27
- •Задача 28
- •Тема 4 Электрический ток. Закон Ома
- •Задача 29
- •Задача 30
- •Задача 31
- •Задача 32
- •Задача 33
- •Задача 34
- •Задача 35
- •Задача 36
- •Задача 37
- •Задача 38
- •Задача 39
- •Задача 40
- •Задача 41
- •Задача 42
Задачи по физике. Электричество и магнетизм. Часть I
Введение
В предлагаемое учебное пособие вошли задачи по курсу общей физики (раздел “Электричество и магнетизм”), предназначенные для студентов физико-математических факультетов педагогических вузов. Задачи разделены по темам в соответствии с действующей программой по общей физике для подготовки бакалавров образования по направлениям “физика”, “математика”, “прикладная математика и информатика” и специалистов соответствующего профиля. В сборнике содержатся задачи трех уровней сложности, что упрощает его использование в сочетании с рейтинговой системой оценки знаний. Задачи первого (низшего) уровня сложности являются типовыми, они снабжены подробными решениями и предлагаются для воспроизведения студентам, претендующим на удовлетворительную оценку. Задачи второго и третьего уровней сложности предназначены для самостоятельного решения студентами, претендующими на более высокий рейтинг, требуют, как правило, проработки дополнительной литературы, и творческого подхода. Учебное пособие может быть полезно также учителям, работающим в школах с углубленным изучением физики и учащимся этих школ.
Тема 1 Закон Кулона Напряженность электрического поля
По закону Кулона сила, действующая между двумя заряженными телами, размеры которых малы по сравнению с расстоянием между ними, определяется формулой:
![]() ,
,
где q1 и q2 – электрические заряды тел,
r – расстояние между ними,
– относительная диэлектрическая проницаемость среды,
0 – электрическая постоянная, равная в СИ 8,8510-12 Ф/м.
Напряженность электрического поля определяется формулой
![]()
где F – сила, действующая на заряд q.
Напряженность поля точечного заряда
![]()
Напряженность электрического поля от нескольких зарядов находится по правилу геометрических сложений полей.
По теореме Гаусса поток напряженности сквозь любую замкнутую поверхность
![]()
где q – алгебраическая сумма зарядов, находящихся внутри этой поверхности.
При помощи теоремы Гаусса можно найти напряженность электрического поля, образованного различными заряженными телами.
Напряженность поля, образованного заряженной бесконечно длинной нитью
![]()
где – линейная плотность заряда на нити,
а – расстояние от нити.
Если нить имеет конечную длину, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из середины нити на расстоянии а от нее равна:
![]()
где – угол между направлением нормали к нити и радиус-вектором, проведенным из рассматриваемой точки к концу нити.
Напряженность поля, образованного заряженной бесконечно протяженной плоскостью
![]()
где – поверхностная плотность заряда на плоскости.
Если плоскость представляет собой диск радиусом R, то напряженность поля в точке, находящейся на перпендикуляре, восстановленном из центра диска на расстоянии а от нее,
![]()
Напряженность поля, образованного разноименно заряженными бесконечными плоскостями
![]()
Напряженность поля, образованного заряженным шаром
![]()
где q – заряд шара радиусом R,
r – расстояние от центра шара, причем r>R.
Задача 1
В вершинах правильного шестиугольника расположены три положительных и три отрицательных заряда. Найти напряженность Е электрического поля в центре шестиугольника при различных комбинациях в расположении этих зарядов. Каждый заряд 1,5 нКл, сторона шестиугольника 3 см.
Дано:
|
Решение: Возможны три варианта расположения зарядов в вершинах шестиугольника. Пусть
Напряженность электрического поля в т. А является векторной суммой напряженностей
|
Ерез – ? |
создаваемых в этой точке положи- |
тельными
и отрицательными зарядами. Эти
напряженности равны по модулю
![]()
Рассмотрим случаи:
а) по принципу суперпозиции
|
(1) |
угол между векторами 2=120.
Т.к.
векторы
![]() и
и
![]() ,
,
![]() и
и
![]() ,
,
![]() и
и
![]() сонаправлены, то их можно сложить.
сонаправлены, то их можно сложить.
A![]()
|
(2) |
-q4
+q2
-q6
+q3




![]()
![]()


 +q1
-q5
+q1
-q5![]()
![]()
![]() ,
она численно равна
,
она численно равна
![]()
Вектор
![]() направлен в противоположную сторону
и, значит, уравнение (2) приобретает вид
направлен в противоположную сторону
и, значит, уравнение (2) приобретает вид
![]()
учитывая,
что
![]() ,
приходим к выводу, что
,
приходим к выводу, что
Ерез=0.
б) используя принцип суперпозиции:
, |
(3) |
векторы
![]() имеют взаимно противоположные направления
и одинаковые значения, и уравнение
приобретает вид:
имеют взаимно противоположные направления
и одинаковые значения, и уравнение
приобретает вид:
Ерез=Е2+Е5=2Е2, |
(4) |
+q1
-q5
+q2
+q3

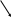 -q4
-q6
-q4
-q6![]()
![]()
![]()
![]()
![]() сонаправлены и имеют равные значения,
лежат на одной прямой.
сонаправлены и имеют равные значения,
лежат на одной прямой.
![]() (5)
(5)
Подставим (5) в (4)
![]()
в) по принципу суперпозиции
|
(6) |
+q3
-q4
+q1
-q6

 +q2
-q5
+q2
-q5![]() ,
и что они численно равны, выражение (6)
можно переписать в виде:
,
и что они численно равны, выражение (6)
можно переписать в виде:
![]()
Результирующий
вектор
![]() лежит на
лежит на
![]() (используя сложение правилом
параллелограмма), угол между векторами
(используя сложение правилом
параллелограмма), угол между векторами
![]() равен 60.
Результирующая напряженность направлена
от А к q5
и равна по модулю
равен 60.
Результирующая напряженность направлена
от А к q5
и равна по модулю
![]()
![]() .
.
Ответ: напряженность в центре шестиугольника при трех вариантах расположения зарядов равна Е=0; Е=30 кВ/м; Е=60 кВ/м, соответственно.

