Порядок выполнения лабораторной работы

1 Синтезировать и сохранить для отчета временные диаграммы сигналов.

2 Определить требуемые значения и графики используя численные методы анализа. Тип метода интегрирования указан в исходных данных.

Содержание отчета лабораторной работе

1 Содержание индивидуального задания. Численные значения параметров.

2 Математические описания и параметры тестовых сигналов, программы их синтеза.

3 Графики исходных сигналов и их суммы. Указывать размерности физических величин.

4 Рассчитанные значения п.п. 1…7 задания №2 занести в таблицу:

Тип сигнала	максимальное значение напряжения, В	среднее значение напряжения, В	…	...
1-й
2-й
3-й
∑

5 Графики скорости изменения сигнала, мощности, энергии исходных сигналов и их суммы. Указывать размерности физических величин.

6 Выводы по результатам работы.

Вопросы к защите лабораторной работы

1 Физическая величина. Тип величины, числовое значение, единицей измерения.

2 Постоянная, переменная, смешанная, случайная величина.

3 Гармоническое колебание. Полигармонический сигнал.

4 Импульс. Последовательность импульсов. Коэффициент скважности и заполнения.

5. Случайные сигналы.

5 Динамическое представление произвольного сигнала посредством функций включения (Хевисайда) и дельта-функций (функции Дирака).

6 Определить размах колебаний величины, максимальное значение величины, среднее значение, средневыпрямленное значение, действующее значение величины, коэффициент формы и амплитуды.

7 Как определить величину мощности электрического сигнала, величину электрической энергии выделяемой на нагрузке, величину средней мощности электрического сигнала?

8 Абсолютный и относительный уровень сигнала. По напряжению (току), по мощности.

9 Дифференцирование непрерывных функций. Физический и геометрический смысл. Постановка задачи численного дифференцирования. Особенность задачи численного дифференцирования.

10 Интегрирование непрерывных функций. Физический и геометрический смысл. Постановка задачи численного интегрирования. Методы численного интегрирования.

Задачи

1 Импульсный сигнал u прямоугольной формы имеет длительность 2 с и амплитуду 3 В. Начало импульса в момент времени t_н=3 с. Записать аналитическое выражение этого сигнала с помощью функций Хевисайда.

2.

Лабораторная работа №2

Корреляционный анализ сигналов Цели лабораторной работы

Исследовать корреляционные свойства простейших сигналов.

Теоретические сведения

Корреляционный анализ

Корреляционный анализ играет большую роль в теории сигналов. Его смысл состоит в количественном измерении степени сходства различных сигналов.

Корреляционная функция

Корреляционная функция (КФ; английский термин — correlation function, CF) детерминированного сигнала с конечной энергией представляет собой интеграл (в бесконечных пределах) от произведения двух копий сигнала, сдвинутых друг относительно друга на время τ.

Корреляционная функция показывает степень сходства между сигналом и его сдвинутой копией — чем больше значение корреляционной функции, тем это сходство сильнее. Кроме того, корреляционная функция обладает следующими свойствами:

1. Значение КФ при τ=0 равно энергии сигнала, то есть интегралу от его квад­рата:

2. КФ является четной функцией своего аргумента т:

.

3. Значение КФ при т = О является максимально возможным значением:

4. С ростом абсолютного значения т КФ сигнала с конечной энергией затухает:

5. Если сигнал s(t) не содержит особенностей в виде дельта-функций, его КФ не может иметь разрывов (то есть обязана быть непрерывной функцией).

6. Если сигнал — напряжение, то размерность его КФ равна В² • с.

В качестве примера вычислим КФ прямоугольного импульса

- при 0<τ< Т

- при -T<τ<0

- при |τ| > Т

Объединяя результаты, можно записать

График КФ прямоугольного импульса показан на рис. 1.26.

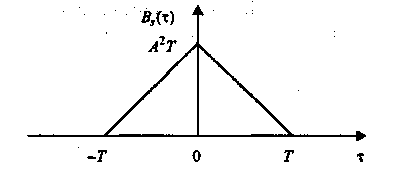
Рис. 1.26. Корреляционная функция прямоугольного импульса

В случае периодического сигнала (и вообще любого сигнала с бесконечной энергией) воспользоваться приведенным определением не удастся. Поэтому КФ периодического сигнала с периодом Т вычисляют, усредняя произведение сдвинутых копий в пределах одного периода:

КФ гармонического сигнала тоже является гармонической функцией. Еще очень важен тот факт, что результат не зависит от начальной фазы гармонического сигнала.

Набор свойств такой КФ несколько меняется.

1. Значение при τ=0 равно не энергии, а средней мощности анализируемого сигнала:

2. Свойство четности сохраняется:

.

3. Значение КФ при τ = 0 по-прежнему является максимально возможным:

4. КФ периодического сигнала является периодической функцией с тем же периодом, что и сам сигнал:

.

5. Если сигнал не содержит дельта-функций, его КФ будет непрерывной функцией.

6. Размерность КФ периодического сигнала — квадрат размерности сигнала (В², если сигнал — напряжение).

Взаимная корреляционная функция

Если КФ показывает степень сходства между сдвинутыми копиями одного и того же сигнала, то взаимная корреляционная функция (ВКФ; английский термин — cross-correlation function, CCF) позволяет измерить аналогичную величину для сдвинутых экземпляров двух разных сигналов.

Общий вид формулы КФ сохраняется, но под интегралом стоит произведение двух разных сигналов, один из которых задержан на время т:

ЗАМЕЧАНИЕ. Очевидно, что КФ является частным случаем ВКФ, когда оба сигнала одинаковы

В качестве примера вычислим ВКФ прямоугольного и треугольного импульсов:

График полученной ВКФ представлен на рис. 1.27.

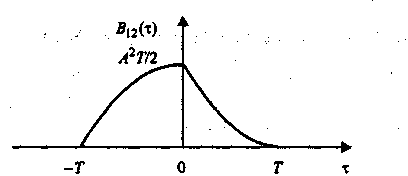
Рис. 1.27. ВКФ прямоугольного и треугольного импульсов

Свойства ВКФ несколько отличаются от свойств КФ:

1. , где Е1 и E2 — энергии сигналов s₁(t) и s₂(t).

2. , то есть изменение знака τ равносильно взаимной перестановке сигналов.

3. Значение ВКФ при τ=0 ничем не выделяется; максимум может быть расположен в любом месте оси τ.

4. С ростом абсолютного значения т ВКФ сигналов с конечной энергией затухает:

5. Если сигналы s₁(t) и s₂(t) не содержат особенностей в виде дельта-функций, то ВКФ не может иметь разрывов (то есть обязана быть непрерывной функцией).

6. Если сигналы — напряжение, то размерность их ВКФ равна В² с.

Для периодических сигналов понятие ВКФ обычно не применяется, хотя оно мо­жет быть введено в случае, если сигналы s₁(t) и s₂(t) имеют одинаковый период.

Литература

1 Цифровая обработка сигналов. А.Б.Сергиенко –СПб.: Питер, 2003. –608с.

2 Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высш. шк., 1988. –448с.