Численные методы

“ЭВМ многократно увеличивает

некомпетентность вычислителя”

Принцип Питера

Дифференцирование

Физическим смыслом производной называют скорость изменения функции на бесконечно малом интервале аргумента.

Геометрическим смыслом производной называют отношение приращения функции к бесконечно малому интервалу приращения аргумента, что соответствует понятию касательной к функции в данной точке. Тангенс угла наклона касательной в данной точке функции – величина производной.

Особенность задачи численного дифференцирования

Когда производную аналитически заданной функции по причине ее сложности искать затруднительно либо выражение для производной приобретает слишком неудобную для применений форму, используют приближенное, или численное, дифференцирование. Этот метод тем более необходим, если исходная функция задана таблично. Один из способов решения задачи дифференцирования — использование интерполяционных многочленов.

Пусть - функция, для которой нужно найти производную в заданной точке отрезка |а; b|, a — интерполяционный многочлен для построенный на отрезке |а; b|. Заменяя интерполяционным многочленом , получим значение производной на отрезке |а; b| как значение производной интерполяционного многочлена, т. е. примем приближенно

Аналогичным путем можно поступать при нахождении значений производных высших порядков функций .

Полагая, что погрешность интерполирования определяется формулой

,

получаем подход к оценке погрешности производной :

т. е. погрешность производной интерполирующей функции равна производной от погрешности этой функции.

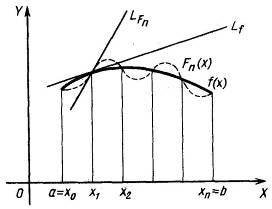
Рисунок 1

Заметим, однако, что задача численного дифференцирования является некорректной. Дело в том, что погрешность производной интерполяционного многочлена может существенно превышать погрешность самой интерполяции. Из рисунка 1 хорошо видно, что даже незначительное отличие (в том числе и совпадение) значений и никак не гарантирует близости значений их производных и ( и — касательные к кривым и соответственно).

В некоторых случаях необходимо найти наклон выпрямленных пар значений, например, когда из выпрямленной скорости надо вычислить ускорение. Для решения этого вопроса можно воспользоваться двумя, рассмотренными ниже, методами.

Разностное отношение

Если измеренные значения в зависимости от параметра получены через интервалы , то при разложении в ряд Тейлора:

можно представить алгоритм вычисления производной как:

( 7 )

Нетрудно заметить, что формула (7) соответствует одному из распространенных определений производной функции и вычисляется как отношение приращения функции к приращению аргумента.

В случае лабораторной работы величина , это не что иное, как период дискретизации сигнала. Например, если частота дискретизации сигнала равна 22050 Гц, то , расстояние между двумя выборками и по временной шкале, будет равно 1/22050 c.

Наклон полинома третьего порядка, построенного по пяти узловым точкам

Согласно (4) через пять точек можно провести полином третьего порядка. Если продифференцировать этот полином по , то получим:

( 8 )

При необходимости, можно вывести формулы, для вычисления значения производной в крайних точках , , и .

Не рекомендуется рассеянные измеренные значения сглаживать с помощью полиномов выше третьего порядка. Полиномы высшего порядка являются причиной пульсации, поэтому наклон сглаживающего полинома сильно отклоняется от измеренного действительного разностного отношения.

Интегрирование

Постановка задачи численного интегрирования

При вычислении определенного интеграла

,

где f(x) — непрерывная на отрезке функция, иногда удается воспользоваться известной формулой Ньютона — Лейбница:

Здесь F(x) — одна из первообразных функций f(x), т. е. такая функция, что F'(x)=f(x). Однако даже в тех, практически редких, случаях, когда первообразную функции удается явно найти в аналитической форме, не всегда удается довести до числового ответа значение определенного интеграла. Если к тому же учесть, что иногда подынтегральная функция вовсе задается таблицей или графиком, то становится понятным, почему интегрирование по формуле Ньютона — Лейбница не получает широкого применения на практике.

В подобных случаях применяют различные методы приближенного (численного) интегрирования. Формулы, используемые для приближенного вычисления однократных интегралов, называют квадратурными формулами. Простой прием построения квадратурных формул состоит в том, что подынтегральная функция f(x) заменяется на отрезке интерполяционным многочленом, например многочленом Лагранжа L_n(x), и получается приближенное равенство

Подобный подход удобен тем, что он приводит к алгоритмам, легко реализуемым на ЭВМ и позволяющим получать результат с достаточной точностью. При этом, естественно, предполагается, что отрезок разбит на n частей точками , наличие которых подразумевается при построении многочлена L_n(x).

Рассмотрим функцию f(x) представленную последовательностью из значений – узловых точек; где взяты через одинаковые интервалы . Для вычисления площади поверхности ограниченной этими узловыми точками можно воспользоваться одним из приведенных ниже методов, причем те из них, которые требуют больше затрат, являются более точными.