Измерение физических величин Основные определения и термины

Амплитуда – максимальное значение синусоидальной переменной величины. Амплитуда, например, как наибольшее из мгновенных значений величины синусоидальной, обозначается .

Величина (физическая величина) – характеристика (свойство) предмета, состояния или процесса, подлежащая измерению.

Каждая величина должна качественно описываться (тип, вид и т.д.) и количественно определяться (значение величины). К примеру, металлы имеют свойство создавать сопротивление электрическому току; сети электропитания характеризуются электрическим напряжением. Их количественные характеристики могут быть измерены. Тип физической величины, особенно в формулах, обозначается буквенным символом, а значение величины как результат измерения обозначается численным значением с единицей измерения.

Физическая величина (ph magnitudes) R=5,6 кОм U=220 В	Тип величины Сопротивление R Напряжение U
	Значение величины 5,6 кОм 220 В	Численное значение (value) 5600 220
		Единица измерения (unit of measurements) Ом В

Зависимость изучаемых параметров от времени характеризуют главным образом постоянной и периодической величинами. Отношение двух однородных величин оценивают относительной величиной.

Величина относительная – физическая или техническая величина, которая определяется через отношение двух величин.

Отношение двух однородных величин представляет собой безразмерную относительную величину, отличающуюся, однако, от обычного числа тем, что имеет признаки и свойства величины, например коэффициент усиления, коэффициент полезного действия. Если в знаменателе стоит исходная (базовая) величина, то название относительной величины часто содержит прилагательное “приведенная” или “нормированная” (величина). Если относительная величина задана в виде логарифма, то говорят о логарифмической относительной величине, например, мера (единица) уровня. Относительная величина отклонения выходного значения обозначается преимущественно в следующих единицах: процент (1%=10^-2), промилле (1‰=10^-3) или миллионная часть (1ppm=1млн^-1=10^-6).

Величина переменная – динамическая величина, среднее значение которой равно нулю.

Переменная величина есть величина колебательная (в основном с периодическим изменением во времени). Ее среднее значение, определенное на большом интервале времени наблюдения (значение постоянное, постоянная величина), равна нулю. Иногда смешанную величину рассматривают как общий случай переменной величины, имеющей ненулевое среднее значение.

Величина периодическая — динамическая величина, изменение мгновенного значения которой имеет периодический характер.

Периодическую величину в общем случае можно математически описать равенством , где t — время; n — любое целое число. Периодическую величину можно представить в виде суммы (статической) постоянной величины (постоянной составляющей периодической величины ) и (периодической) переменной величины, переменной составляющей x(t) (рис. 11): .

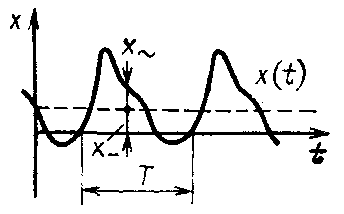
Рис. 1. Величина периодическая: — постоянная составляющая; — переменная составляющая; Т — длительность периода

Величина постоянная — постоянный процесс. Величина (или процесс), мгновенные значения которой в течение периода наблюдения не изменяют свой знак. Статическая постоянная величина имеет постоянное во времени мгновенное значение (например, постоянное напряжение или постоянный ток). Пульсирующая постоянная величина характеризуется изменением во времени мгновенного значения при неизменном знаке (например, выпрямленное переменное напряжение, пульсирующий постоянный ток). В общем случае постоянная величина обозначается добавлением к соответствующему символу горизонтального штриха, например, . В тех случаях, когда символ трактуется однозначно и путаница исключается, допускается использование в качестве обозначения постоянных величин заглавных букв без дополнительных индексов (например, J — переменный ток, I — постоянный ток).

Величина промежуточная — промежуточное значение, более широкая трактовка. Величина, в которую преобразовывается измеряемая или другая величина с целью дальнейшей обработки сигнала.

Величина промежуточная часто встречается в измерительной технике. Особенно наглядно она проявляется при электрическом измерении неэлектрических величин. Так, например, при измерении температуры с помощью термометра сопротивления и магнитоэлектрического измерительного механизма изменение температуры (измеряемая величина) преобразуют в изменение сопротивления, напряжения, тока (промежуточная величина).

Величина синусоидальная — синусоидальное колебание, прежнее название — гармоническое колебание. Переменная величина, мгновенное значение которой изменяется во времени по синусоидальному закону.

Чисто синусоидальную величину можно математически описать в общем случае уравнением вида

где — амплитуда синусоидальной величины; ω— круговая частота и φ — (начальный) фазовый угол. Важными параметрами являются эффективное значение ( , ), средневыпрямленное значение и размах колебаний ( ).

Рис. 12. Величина синусоидальная:

х — амплитуда; — эффективное значение; — средневыпрям-

ленное значение; - размах колебаний (значение от пика до пика); Т — длительность периода; φ — начальный фазовый угол

Многофазную синусоидальную величину образуют несколько однотипных синусоид равной частоты с различными амплитудами и начальными фазовыми углами. Величину, похожую на синусоидальную, но у которой изменяются амплитуда, круговая частота или/и начальный фазовый угол, называют квазисинусоидальной. К ним относятся, например, пульсирующие величины, модулированные синусоиды, экспоненциально нарастающие или спадающие синусоиды.

Величина смешанная — динамическая величина, мгновенное значение которой изменяется во времени как по размеру, так и по знаку (направлению).

Смешанная величина является обычной переменной величиной. Ее среднее значение за время наблюдения, иначе говоря, постоянное значение отлично от нуля. На эту постоянную составляющую наложено переменное колебание.

Отношение эффективного значения переменной составляющей к постоянной составляющей смешанной величины называют пульсацией (или коэффициентом пульсаций ): . В электротехнике периодически изменяющиеся во времени напряжения и токи, содержащие постоянную составляющую, а также постоянное напряжение (ток) с наложенными колебаниями называют смешанными напряжениями или токами.

Рис. 13. Величина смешанная:

— среднее значение; - амплитудное значение; — наименьшее значение; — размах колебаний или значение от пика до пика; Т — длительность периода

Величина числовая — физическая величина, измеряемая путем счета и служащая для количественной характеристики множеств. При этом определяется количество единиц, содержащихся в данном множестве. Признаком числовой величины в словосочетаниях является слово “число” (“количество”), например, число оборотов, число (количество) событий, число (количество) витков.

Время нарастания – разность между двумя моментами времени, в которые импульсная величина принимает наперед заданные мгновенные значения.

Когда форма импульса специально не регламентируется, то временем нарастания T_r называют время между значениями 10 и 90% амплитуды на нарастающем участке. Время спада T_f аналогично на спадающем участке.

Градуировочная характеристика – закон следования градуировочных отметок на аналоговой шкале.

В зависимости от значения каждого деления шкалы различают градуировку, кратную1, 2 и 5.

При градуировке с основанием 1 цена деления шкалы равняется 1 или , где , каждая 5-я, 10-я или 20-я отметка шкалы может иметь численное значение. Если численное значение деления шкалы равняется, например 0,2, 2, 20, то говорят о градуировке с основанием 2. При этом каждая 5-я, 10-я или 20-я отметка шкалы должна иметь численное значение. Аналогично при цене деления, кратной 5, говорят о градуировке с основанием 5, причем каждая 4-я, 10-я или 20-я отметка шкалы имеет численное значение. По отношению к линейности градуировочной характеристики различают линейные и нелинейные шкалы.

Длительность импульса – интервал времени, в течении которого мгновенное значение импульса существенно отличается от нуля.

Длительность импульса в каждом конкретном случае может определяться по-разному. Так, в качестве длительности импульса может быть выбран интервал времени, в течение которого мгновенное значение превосходит заданный или выбранный уровень (например, 10% амплитудного значения). Если уровень составляет 50% от амплитуды импульса, то говорят о длительности импульса на уровне 0,5. Допускается регламентировать длительность реального импульса через длительность равновеликого по площади или энергии прямоугольного импульса с равной амплитудой. Способ определения должен указываться вместе с измеренным значением.

Длительность периода (длительность колебания) – наименьший промежуток времени, по прошествии которого периодически изменяющаяся величина повторяет свои значения. Величиной, обратной длительности периода, является частота.

Единица измерений – установленный соглашением (международным) определенный размер физической величины, служащий для сравнения значений физической величины.

В соответствии с международной системой единиц (СИ) единица измерений имеет числовое значение 1, а приставки (милли, микро, кило, мега и др.) служат для образования дольных и кратных единиц измерения. Обозначение единицы измерения характеризует сущность физической величины, например, символ «В» свидетельствует, что измеряемой величиной является напряжение (см. Обозначения единиц измерения). Относительные и счетные величины имеют специальные единицы измерений.

Значение максимальное (наибольшее значение) – наибольшее значение, которое может принимать мгновенное значение периодической величины. Обычно обозначается . Если наблюдается переменная величина синусоидальной формы, то допускается максимальное значение обозначать как амплитуду.

Значение мгновенное – значение изменяющейся во времени величины в определенный момент времени. Мгновенное значение обозначается маленькими буквами, например . Аргумент t может быть опущен, если обозначение временной зависимости маленькой буквой не имеет двусмысленного толкования, например, u.

Значение наименьшее – наименьшее значение, которое может принимать мгновенное значение периодической величины. Обычно обозначается .

Значение пиковое – амплитудное значение, имеющее место в течение очень короткого (по сравнению с длительностью периода) интервала времени.

Значение постоянное (среднее арифметическое значение периодической величины) – усредненное по времени среднее арифметическое значение периодической величины в течение одного периода или интервала наблюдения для случайной величины

.

Для дискретных сигналов

,

где N – количество отчетов(выборок) сигнала,

x(i) – значение i-й выборки сигнала.

У постоянных величин мгновенное значение и постоянное значение совпадают. Смешенная величина имеет отличное от нуля постоянное значение. У переменных величин постоянное значение равно нулю, например, синусоида. В этом случае говорят о средневыпрямленном значении.

Значение средневыпрямленное – усредненное по времени среднее арифметическое абсолютного значения периодической величины в течение одного периода или интервала наблюдения для случайной величины

.

Для дискретных сигналов

,

где N – количество отчетов(выборок) сигнала,

x(i) – значение i-й выборки сигнала.

Значение численное – число, показывающее, как много единиц измерения содержится в наблюдаемой величине. Значение численное, стоящее перед единицей измерения, является составной частью значения величины. Оно представляет собой отношение измеряемого значения и единицы измерения и характеризует размер (количество) величины. Например, напряжение в электрической сети (220*1В) имеет численное значение 220. В зависимости от выбранной единицы измерения численное значение может быть различным (например, скорость транспортного средства 50,04 км/ч=13,9 м/с)/

Значение эффективное. Эффективное (действующее) значение– среднее квадратическое значение периодической величины в течение одного периода или интервала наблюдения для случайной величины

.

Для дискретных сигналов

,

где N – количество отчетов(выборок) сигнала,

x(i) – значение i-й выборки сигнала.

Эффективное значение переменной во времени величины вызывает за время наблюдения такой же эффект (например, тепловое воздействие тока или величина вращающего момента), как значение постоянной величины.

Таблица . Соотношение между эффективным, средневыпрямленным и амплитудным значениями различных форм периодических сигналов

Формы сигналов	Коэф. формы	Коэф. ампл.	Формулы для расчетов
«Синусоида»
«Меандр»		1
«Прямоугольные видеоимпульсы»
«Треугольник»

Коэффициент амплитуды – отношение амплитудного значения к эффективному значению переменной величины.

Коэффициент передачи (усиления или ослабления) – отношение значения выходной величины к значению входной величины передаточного звена. Обычно используется отношение напряжений (коэффициент передачи по напряжению), а также по току, мощности. .

Коэффициент передачи задается в виде безразмерного числа или в единицах передачи, дБ (см. Уровень передачи). Если коэффициент передачи меньше единицы, речь идет об ослаблении или «подавлении» (разговорное).

Коэффициент формы – отношение эффективного значения к средневыпрямленному значению переменной величины.

Последовательность импульсов – динамическая величина, из одинаковых импульсов периодически повторяющихся импульсов. Параметрами являются амплитуда импульсов, длительность периода и частота(следования импульсов). В случае последовательности прямоугольных импульсов отношение периода Т к длительности импульсов τ называют скважностью

.

Обратную величину называют коэффициентом заполнения g. Различают немодулированные и модулированные последовательности. С заполнением импульса другой динамической величиной (например, гармоническим колебанием – «радиоимпульсы») и без заполнения («видеоимпульсы»).

Частота – количество колебаний периодически изменяющейся величины в единицу времени.

Буквенное обозначение f. Единица измерения 1Гц=1/c; f=1/T, где Т – длительность периода изменения величины. Частота есть в общем случае величина , обратная длительности периода.

При несинусоидальной форме колебаний за основную частоту (первую гармонику) принимается величина, обратная наибольшей длительности периода. Целые кратные значения называют гармоническими частотами (высшими гармониками): f_n=nf. Субгармоническая частота определяется как целая дробь от основной частоты: f_1/n=f/n. Круговая частота (или угловая частота) ω есть скорость изменения угла . При изменении угла на целый круг (полный оборот) ( ) в течение одного периода справедливо равенство . При постоянной частоте справедливо равенство .

Численные значения шкалы – численные значения, соответствующие градуировочным отметкам.

Для определения измеренного значения (основные) градуировочные отметки в соответствии с градуировочной характеристикой имеют численные значения шкалы, у размерных шкал эти числа соответствуют определенным значениям измеряемой величины, а у безразмерных шкал – только порядковому числу градуировочной отметки. У электроизмерительных приборов отдельное численное значение должно содержать не более четырех цифр. Численные значения представляются целыми числами или десятичными дробями.

Уровень – логарифм относительной величины, в знаменателе которой стоит исходная (базовая) величина.

Если логарифмируется отношение двух энергетических величин (главным образом, мощностей) или параметров поля (например, напряжение ,ток, звуковое давление), то логарифмируемое отношение (величин) сохраняется. Используемый при логарифмировании базис обозначается с помощью соответствующего коэффициента и с добавлением обозначений, имеющих смысл единиц измерения. Используются как натуральные (ln с основанием e=2.718), так и десятичные логарифмы. В первом случае единицу измерения называют непер (Нп), во втором случае – бел (Б) или децибел(дБ), 10ºдБ =1Б. Для перевода одной единицы в другую служит следующее соотношение: 1ºдБ=0,1151ºНп или 1ºНп=8,686ºдБ.

Понятием относительный уровень пользуются в тех случаях, когда, например, мощность, ток или напряжение сигнала в какой-то точке канала передачи (P_x, I_x, U_x) сравниваются с аналогичной величиной в выбранной условной точке (P₁, I₁, U₁). В общем случае такой условной точкой выбирается вход канала передачи. Если же в качестве базовой используется постоянная и независимая условная точка (базовое или опорное значение), то говорят об абсолютном уровне.

В общем случае в качестве относительного принято значение мощности P₀=1ºмВт (мощность образцового генератора или милливатного передатчика с внутренним сопротивлением R_i=600ºОм), или напряжения (U₀=0,775ºВ), или тока (I₀=1,29 мА), которые выделяют на сопротивлении 600ºОм мощность 1ºмВт или 1ºмВ∙А. В качестве условного значения звукового давления принято значение p₀=20ºмкПа. В радиоприемной технике иногда используется базовое значение напряжения в 1мкВ, а уровень обозначается дБмкВ.

Таблица Уровни

Уровень	Определение	Единица измерения
Относительный уровень мощности		дБ
		Нп
Относительный уровень напряжения		дБ
		Нп
Абсолютный уровень мощности		дБ/ 1ºмВт
		Нп/ 1ºмВт
Абсолютный уровень напряжения		дБ/ 0,775ºВ
		Нп/ 0,775ºВ
Уровень тока	Аналогично уровню напряжения при I0=1,29 мА

Уровень передачи – характеристика свойств объекта или системы с помощью уровня. Уровень передачи четырехполюсника выражается логарифмом отношения (эффективных значений, если не указаны другие величины) входного напряжения U₁ и выходного напряжения U₂, или соответствующих токов (I₁ ,I₂), или мощностей (P₁ ,P₂), и выражается в децибелах (дБ) или реже в неперах (Нп).

Если входная величина больше выходной, то положительный знак уровня передачи указывает на наличие ослабления (подавления) сигнала. В противном случае (выходная величина больше входной) знак уровня передачи отрицательный, т.е. имеет место усиление. Однако на практике оказывается удобным пользоваться всегда положительными значениями как ослабления, так и усиления.

Таблица Ослабление или усиление

Параметр	Определение	Соотношение величин входных и выходных
Ослабление мощности
Усиление мощности
Ослабление напряжения
Усиление напряжения
Ослабление и усиление тока	Аналогично ослаблению и усилению напряжения

Уровень. Практическое использование. Итак, децибелом (дБ) называется мера отношения между двумя уровнями сигнала:

,

где

— усиление в децибелах; — мощность на входе; — мощность на выходе; lg — логарифм по основанию 10.

Связь между значениями в децибелах и степенями числа 10 показана в таблице.

Таблица Значения в децибелах

Отношение мощностей	дБ	Отношение мощностей	дБ
101	10	10-1	-10
102	20	10-2	-20
103	30	10-3	-30
104	40	10-4	-40
105	50	10-5	-50
106	60	10-6	-60

В литературе наблюдается некоторая несогласованность в употреблении терминов "усиление" и "ослабление". Если значение G_dB положительно, оно означает на практике увеличение мощности. Например, усиление 3 дБ означает, что мощность сигнала удвоилась. Если же значение G_dB отрицательно, оно означает на практике уменьшение мощности. Например, усиление -3 дБ означает, что мощность уменьшилась вдвое, т.е. произошло ослабление. Обычно при этом говорят, что имеется ослабление 3 дБ. Однако, согласно некоторым источникам, эта величина должна называться усилением -3 дБ. Более правильно будет сказать, что отрицательное усиление соответствует положительному ослаблению. Таким образом, ослабление в децибелах определяется как

.

Пример. Если на входе линии передачи уровень мощности сигнала составляет 10 мВт, а на некотором расстоянии — 5 мВт, то ослабление сигнала можно выразить следующим образом:

L_dB = 10 lg(10/5) = 10 (0,3) = 3 дБ.

Отметим, что в децибелах выражается относительное, а не абсолютное отличие. Ослабление сигнала с 1000 мВт до 500 мВт также является ослаблением на 3 дБ. Децибелы используются и для измерения отношения напряжений, учитывая тот факт, что мощность пропорциональна квадрату напряжения:

,

где P — мощность, рассеиваемая на сопротивлении R; U — напряжение на сопротивлении R.

Следовательно,

Суммарное усиление или ослабление сигнала в каскадном канале передачи можно вычислить с помощью простых операций сложения и вычитания.

Пример. Использование децибелов полезно при определении усиления или снижения мощности, происходящего на последовательности передающих элементов. Рассмотрим, например, последовательность элементов, на вход которого подается мощность 4 мВт, первый элемент является линией передачи с ослаблением 12 дБ (усилением -12 дБ), второй элемент — это усилитель с усилением 35 дБ, а третий — линия передачи с ослаблением 10 дБ. Суммарное усиление равно (-12 + 35 - 10) = 13 дБ. Вычислим мощность на выходе:

G_dB= 13= 10 1g(P_in/4мBт),

Р_out = 4 · 10^1,3 мВт = 79,8 мВт.

Значения в децибелах связаны с относительными амплитудами или изменениями амплитуд, но никак не с абсолютными уровнями. Было бы удобно передать абсолютный уровень мощности также в децибелах, чтобы можно было легко вычислять усиление или снижение мощности по отношению к исходному сигналу. Единица дБВт (dBW - децибел-ватт) широко используется в приложения СВЧ-связи. В качестве эталонного уровня выбрана величина 1 Вт, и ей присвоено значение 0 dBW. Абсолютный уровень мощности в децибел-ваттах определяется следующим образом:

мощность, .

Пример. Мощности 1000 Вт соответствует 30 дБВт, а мощности 1 мВт соответствует минус 30 дБВт.

Широко используется другая производная единица — дБмВт (dBmW или просто dBm, децибел-милливатт). В этом случае за эталонный уровень мощности принимается 1 мВт, 0 дБмВт соответствует 1 мВт. Следовательно,

мощность,

Полезезно запомнить следующие соотношения:

+30 дБмВт = 0 дБВт, 0 дБмВт = -30 дБВт.

Энергия – физическая и техническая величина в электрических цепях, выражаемая как произведение мощности на единицу времени. Если в электрической цепи напряжение u и ток i являются переменными величинами, то получаемая мощность, отнесенная к конкретному моменту времени (мгновенная мощность), является произведением тока и напряжения.

Энергия, иначе, способность производить работу, выражается мощностью, выделяемой в течение определенного промежутка времени. Электрическая энергия или работа определяется поэтому произведением электрической мощности и времени. Это относится как к переменному току ( например, трехфазному) току, так и к постоянному. Единицей измерения электрической энергии в системе СИ является джоуль. Кроме того, используется ватт∙секунда и кратные ей величины (например, кВт∙ч).

Таблица Уравнения для вычисления потребленной энергии

Энергия или работа	Однофазный переменный ток	Симметрично нагруженная трехфазная сеть	Единица измерения
Полная переменного тока
Активная составляющая
Реактивная составляющая
Постоянного тока		-