Непрерывность функции, разрывы [Данко п.Е., Попов а.Г., Кожевникова т.Я. Высшая математика в упражнениях и задачах (часть 1)]

Пусть функция f(x) определена на некотором множестве Е и х₀ – предельная точка множества Е.

Функция f(x) называется непрерывной в точке х₀, если

1. Она определена в точке х₀

2. Существует конечный предел

3. Этот предел равен значению функции в точке х_0.

Иначе говоря, функция у=f(x) называется непрерывной в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, то есть

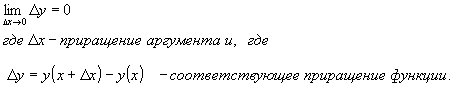
Разрывность функции

Итак, если хотя бы одно из трех условий непрерывности не выполняется, функция называется разрывной в точке х₀, а сама точка x₀-точкой разрыва. Если в точке x₀ оба односторонних предела существуют и конечны, то разрыв называется разрывом первого рода. Пусть х₀-точка разрыва первого рода, т.е.

Возможны два случая

1. f(x₀+0)=f(x₀-0)=L, но либо функция f(x) не определена в точке х₀, либо f(x₀) # L (то есть не выполнено либо первое либо третье условие непрерывности). В этом случае разрыв называется устранимым, так как если доопределить функцию в точке х₀ или переопределить ее, положив f(x₀)=L, функция f(x) станет непрерывной в точке х₀.

оба односторонних предела существуют, конечны и равны.

2. f(x₀- 0) не равна f(x₀+0). B этом случае разрыв называется неустранимым.

Если же хотя бы один из односторонних пределов f(x₀+0) или f(x₀-0) не существует или бесконечен, то разрыв называется разрывом второго рода. Разрыв второго рода всегда неустранимый.

Если в точке х₀ функции f(x) и g(x) непрерывны, то в этой же точке непрерывными являются и функции

Свойство нерерывности сложной функции

Если функция u=g(x) непрерывна в точке х₀ и функция y=f(u) непрерывна в точке u₀=g(x₀), то сложная функция y=f(g(x)) непрерывна в точке х₀.

Основные элементарные функции непрерывны во всех точках своей области определения.

Таким образом, всякая элементарная функция, т.е. функция, составленная из основных элементарных, с помощью конечного числа алгебраических действий и композиций, является непрерывной во всех точках своей области определения.

Функция непрерывна на отрезке, если она непрерывна во всех точках отрезка.

Рассмотрим на примере, исследуем функцию:

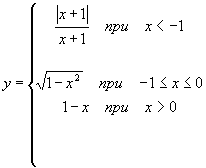
на непрерывность, найдем точки разрыва и их тип. Построим схематический график функции. Данная функция определена на всей числовой оси.

ПРОИЗВОДНАЯ ФУНКЦИИ

Нахождение производной

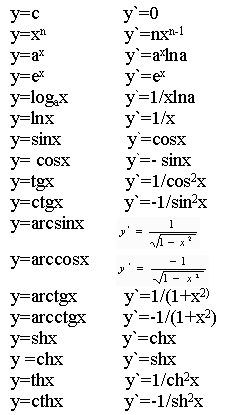
Связь непрерывности и дифференцируемости функции

Из уже известных нам свойств пределов очевидно, что если функция у(x) имеет конечный предел , то предел произведения этого соотношения на бесконечно малую тем более конечен и, более того, равен нулю.

,

а – это означает непрерывность функции. То есть если функция дифференцируема, то она непрерывна.

То, что обратное неверно, видно из примера:

Рассмотрим функцию

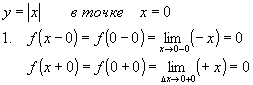
Предел слева существует, конечен и равен пределу справа, и значение функции в точке совпадает со значением предела.

Следовательно, функция непрерывна в нуле.

2. Выражение для производной функции у

.

Имеет в точке x=0 левый предел (-1), а правый предел – (+1), а это означает, что предела она не имеет, то есть производной в точке х=0 не существует.

Видим, что функция, непрерывна в точке х=0, производной в этой точке не имеет.

Приложение Б

Условные обозначения

Описание динамически изменяющихся величин:

x(t), s(t)-одномерный сигнал

Производные от динамически изменяющихся величин:

- первая производная,

- вторая производная,

Обычно используют греческие буквы для обозначения статистик модели и латинский буквы для соответствующей статистики выборки, т.е. μ и m( или M), σ и s.

Также,

- среднее значение выборки

Список основных символов и сокращений

u(t) – напряжение,

i(t) – ток,

p(t) – мощность,

e(t) – энергия.

Приложение

Теоретические основы преобразования сигналов