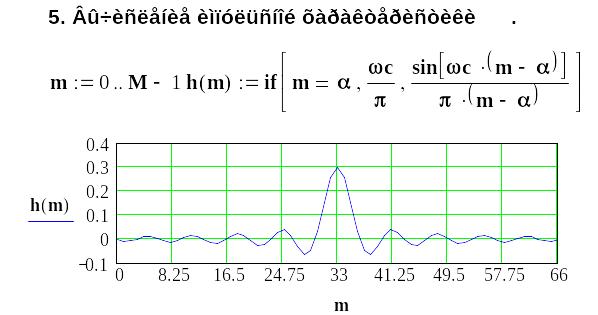
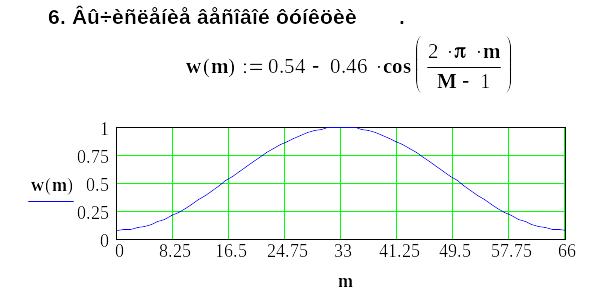
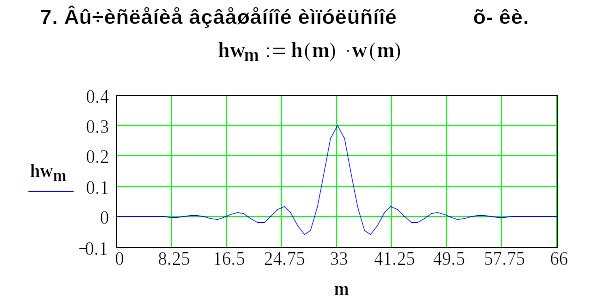
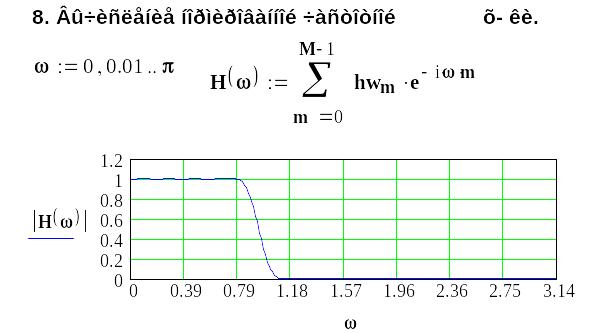
3 Методика синтеза ких-фильтров с использованием рядов Фурье

Методику синтеза обсудим на примере проектирования фильтра нижних частот.

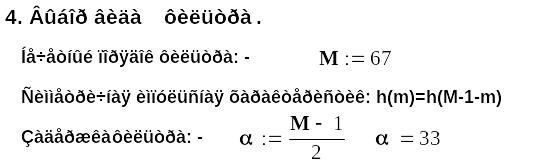
10. Проверяем достижение требований частотной

характеристики цифрового фильтра.

8.4 Синтез КИХ-фильтров методом частотной выборки

Пусть требуемая частотная характеристика цифрового фильтра. Положим, что порядок синтезируемого фильтра равен .

Взяв частотные выборки с частотной характеристики синтезируемого цифрового фильтра с шагом можно получить:

, (8.7)

где: комплексные отсчеты:

(8.8)

1 , если - в полосе пропускания

0 , если - в полосе заграждения

Чтобы получить действительную импульсную характеристику и частотную характеристику с линейной фазой необходимо:

• должны быть симметричными по амплитуде ;

• линейную антисимметричную фазу на интервале .

Фильтр вида-А: , — нечётное.

(8.9)

Учитывая (8.9) в обратном ДПФ (4.7), получим:

(8.10)

Реальная частотная характеристика фильтра:

• Аппроксимация частотной характеристики с помощью частотных выборок функций неудовлетворительна.

• уменьшение ошибки можно получить за счет введения переходной полосы и взятия в ней частотных выборок отличающихся от 0 или 1.

• Уменьшение ошибки можно достичь с помощью весовых оконных функций.

Достоинства метода

• Синтез фильтра с произвольным видом частотной характеристики.

8.5 Методика синтеза ких-фильтров с использованием частотных выборок

Методику синтеза обсудим на примере синтеза фильтра нижних частот:

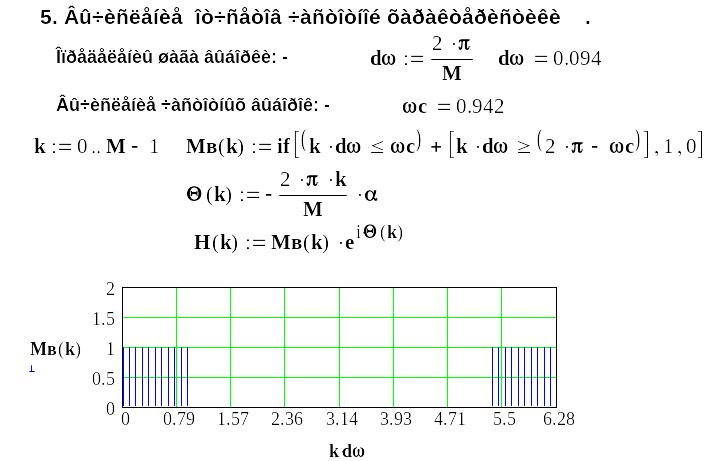
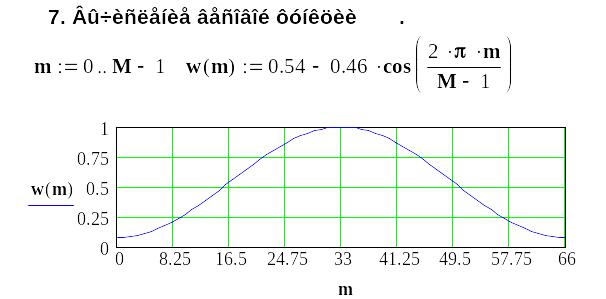
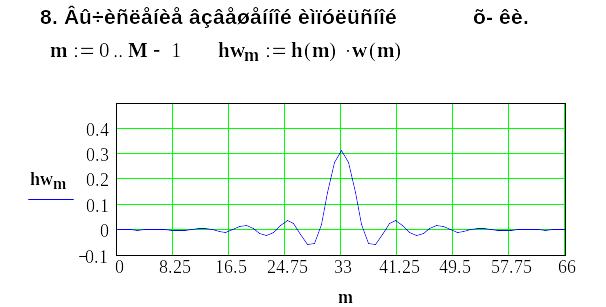
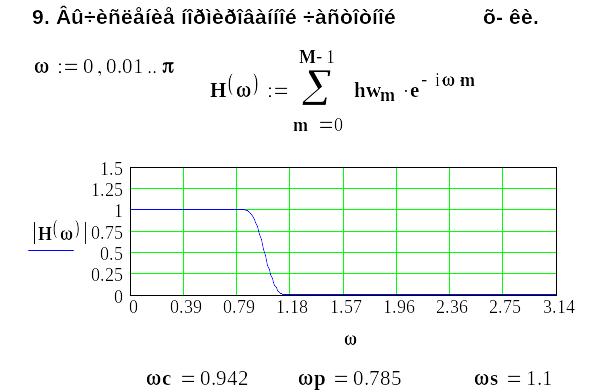
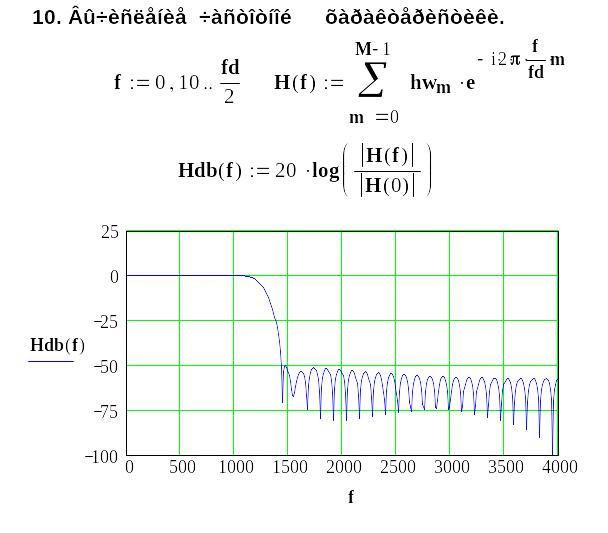
11. Проверяем достижение требований частотной

характеристики цифрового фильтра.

Литература

1 Гутников В.С. Фильтрация измерительных сигналов. -Л.: Энергоатомиздат. Ленингр. отд-ние, 1990. – 192 с.: ил.

2 Цифровая обработка сигналов. А.Б.Сергиенко –СПб.: Питер, 2003. –608с.

Исходные данные к лабораторной работе

Таблица

n/n	Метод синтеза фильтра	Тип базового фильтра	Ds, дБ
1	взвешивания	ФНЧ	10
2	частотных выборок	ФВЧ	20
3	взвешивания	ФПЗ	30
4	частотных выборок	ФНЧ	40
5	взвешивания	ФВЧ	50
6	частотных выборок	ФПЗ	10
7	взвешивания	ФНЧ	20
8	частотных выборок	ФВЧ	30
9	взвешивания	ФПЗ	40
10	частотных выборок	ФНЧ	50
11	взвешивания	ФВЧ	10
12	частотных выборок	ФПЗ	20
13	взвешивания	ФНЧ	30
14	частотных выборок	ФВЧ	40
15	взвешивания	ФПЗ	50
16	частотных выборок	ФНЧ	10
17	взвешивания	ФВЧ	20
18	частотных выборок	ФПЗ	30
19	взвешивания	ФНЧ	40
20	частотных выборок	ФВЧ	50
21	взвешивания	ФПЗ	10
22	частотных выборок	ФНЧ	20
23	взвешивания	ФВЧ	30
24	частотных выборок	ФПЗ	40
25	взвешивания	ФНЧ	50

Тип базового фильтра – фильтр, который используется для реализации заданного (полосового). Т.е. если указан тип фильтра НЧ, следовательно, необходимо определить структурную схему фильтра ПП, состоящего из нескольких ФНЧ с разными частотами среза и сумматоров, которые обеспечат получение желаемой частотной характеристики полоснопропускающего фильтра(ФПП)

Условные обозначения:

Ds - уровень ослабления сигнала в полосе заграждения

Содержание лабораторной работы

Задание №1: Определить необходимую частотную характеристику полосового нерекурсивного фильтра выделяющего гармоническую составляющую суммарного сигнала (исходные данные к лабораторной работе №1). Т.е. гармонический сигнал считается полезным, а остальные составляющие являются помехами и их необходимо удалить из суммарного сигнала.

Задание №2: Определить структуру системы для реализации необходимого полосового фильтра из заданного типа фильтра(ФНЧ, ФВЧ, ФПЗ). Определить коэффициенты нерекурсивного фильтра. Тип частотной характеристики базового фильтра и метод синтеза задан в исходных данных к работе.

Задание №3: Исследовать характеристики базового фильтра и фильтра для выделения гармонического сигнала.

Задание №4: Представить результаты применения фильтра во временной и частотной области.