Лабораторна робота №3

Проходження керуючих сигналів через лінійні кола

Мета роботи - Дослідження процесів проходження керуючих сигналів

через лінійні кола . процеси диференціювання та інтегрування сигналів

1. Основні позначення, розрахункові формули і означення

При аналізі передачі складних сигналів через лінійні радіотехнічні кола використовується принцип суперпозиції. Відповідно до цього відгук на виході лінійного кола на сумарний вплив дорівнює сумі відгуків на кожен вплив.

Шляхом гармонійного аналізу вхідного впливу можна визначити його спектральну характеристику, тим самим складний вхідний вплив аналітично представляється сукупністю найпростіших впливів (гармонік). Для визначення відгуку кола (вихідного сигналу) необхідно ще знати передаточну функцію кола. Передаточна функція кола – це відношення комплексних амплітуд вихідного сигналу до вхідного при гармонійному сигналі на вході:

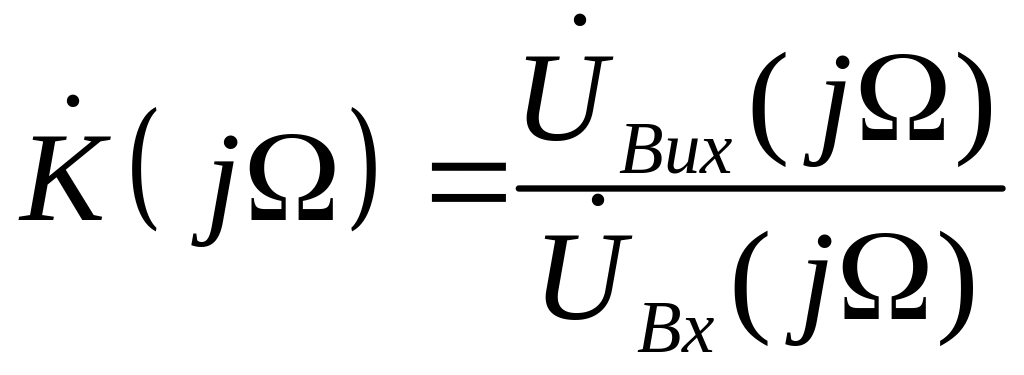
Оскільки – величина комплексна, то модуль передаточної функції визначає амплітудно-частотну характеристику кола, а аргумент – фазочастотну характеристику. Ідеальні кола мають рівномірну АЧХ і лінійну ФЧХ .

Метод аналізу передачі сигналів через лінійні кола, заснований на гармонійному розкладанні сигналів і визначенні передаточної функції, називається спектральним і включає наступні етапи:

• якщо вхідний вплив 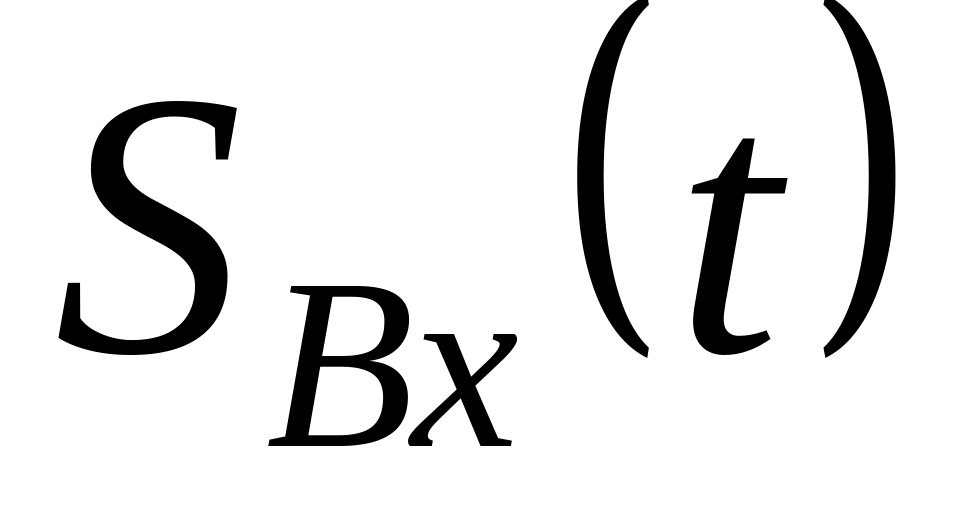, то його спектральна щільність визначається виразом ;

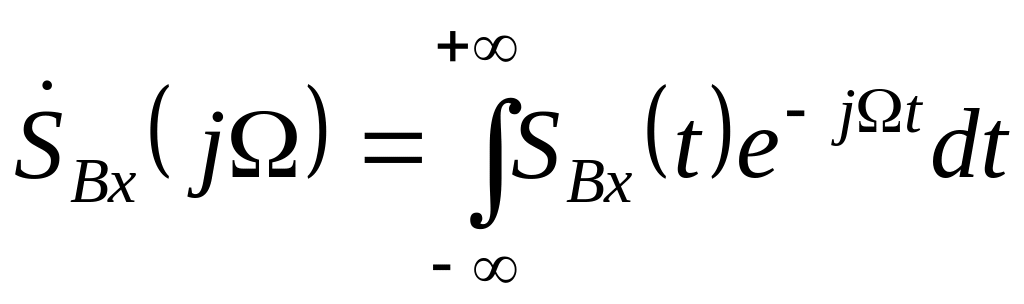• передаточна функція кола – ;

• спектр вихідного сигналу ;

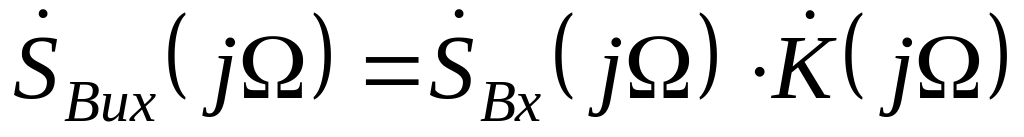• вихідний сигнал знаходиться на основі зворотному перетворення Фур'є

.

Замість перетворення Фур'є для обчислення вихідної напруги можна використовувати перетворення Лапласа:

, де .

Якщо вхідний вплив представляють у виді сукупності стрибків ( імпульсів) напруги, то вихідний сигнал (відгук кола) визначається за методом інтеграла накладення. При цьому необхідно знати перехідну ( імпульсну) характеристику кола. Перехідна характеристика кола – це відгук кола на одиничний стрибок напруги (чи струму).

Представимо вхідний вплив у виді суми стрибків малої величини, що запізнюються по відношенню один до одного і стрибка при t = 0 ( рис.1.1).

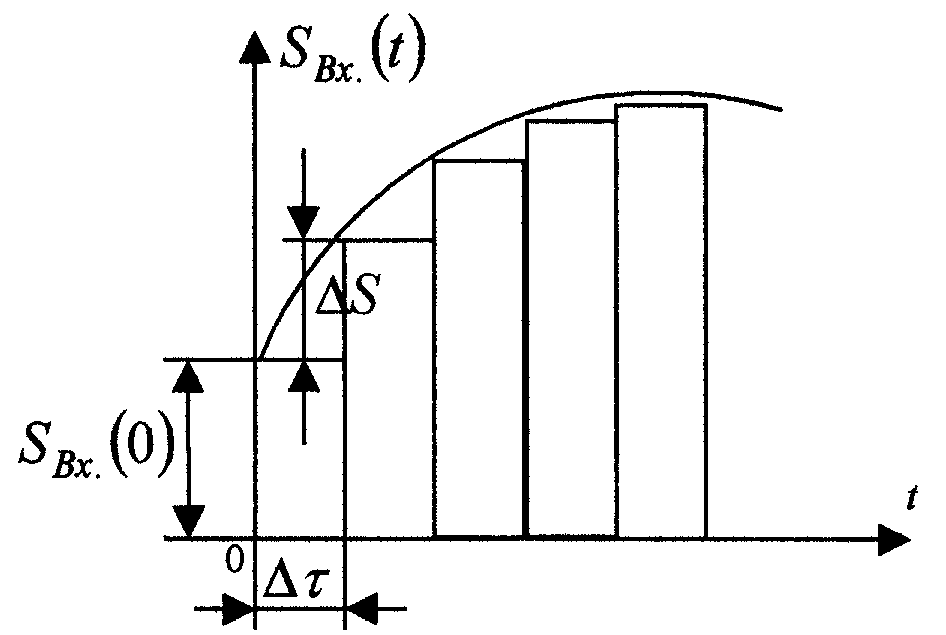
Рисунок 1.1 - Представлення вхідного сигналу у вигляді сукупності стрибків

Реакція кола на перший стрибок дорівнює відгуку кола на одиничний стрибок [тобто перехідній характеристиці ], помноженої на висоту стрибка , реакція на зміщений стрибок – . Тут ΔS – висота стрибка, η(t – Δτ) – перехідна характеристика, зміщена убік запізнювання на Δτ. Отже, для розглянутого моменту часу t = K · Δτ відгук кола

.

при n → ∞ і Δτ → 0 отримаємо наступний вираз у вигляді інтегралу Дюамеля

або

Якщо представити вхідний сигнал сукупністю великого числа коротких імпульсів (див. рис.1.2), то реакцію кола визначають через імпульсну характеристику.

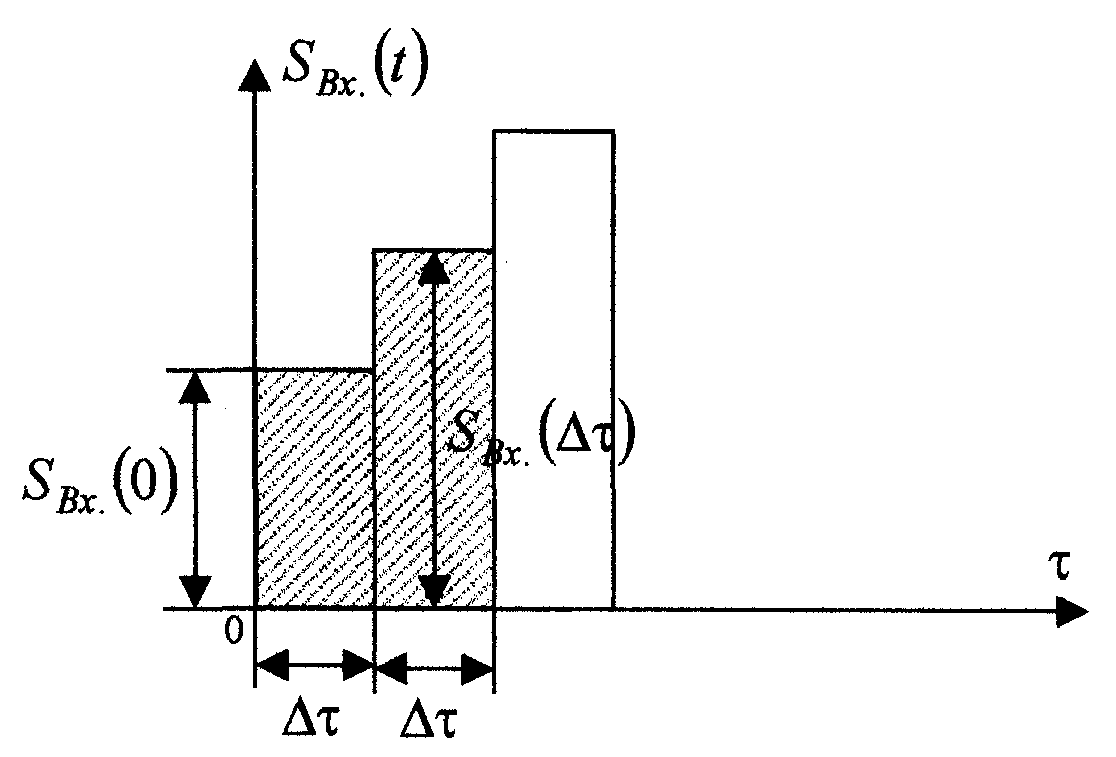
Рисунок 1. 2- Представлення вхідного сигналу у вигляді сукупності імпульсі

Імпульсна характеристика q(t) – це відгук кола на одиничний  - імпульс. Реакція кола на перший імпульс дорівнює реакції на одиничний імпульс (тобто імпульсній характеристиці q(t) ), помноженій на площу імпульсу ; реакція кола на другий імпульс , де через S_вх() позначено площу другого імпульсу, q(t - ) – імпульсна характериcтика, що відповідає моменту .

Відгук кола для моменту t = n   становитиме .

Коли виконати граничний перехід при п → ∞ і ∆τ → 0, то отримаємо

Передаточна функція є спектральною (частотною) характеристикою, а перехідна й імпульсна характеристики – часові характеристики. Усі ці характеристики зв'язані між собою:

• а) імпульсна характеристика і передаточна функція: ,

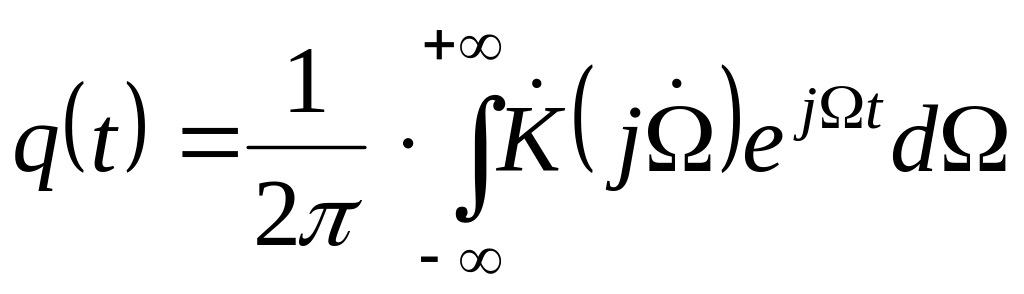де імпульсна характеристика визначена як відгук кола на δ – функцію спектральним методом;

• імпульсна і перехідна характеристика - ,тобто імпульсна характеристика дорівнює похідній від перехідної;

• перехідна характеристика і передатна функція:

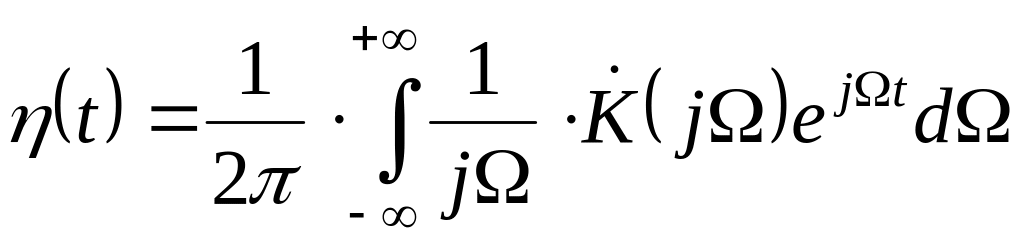
В иходячи з цього зв'язку можна визначити одну характеристику через іншу. Нехай, наприклад, передаточна функція RС - кола (див. рис. 1.3) має вигляд .

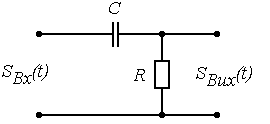
Рисунок 1.3 – Схема найпростішого RС- кола

Перехідна характеристика

;

або в операторній формі:

Імпульсна характеристика:

З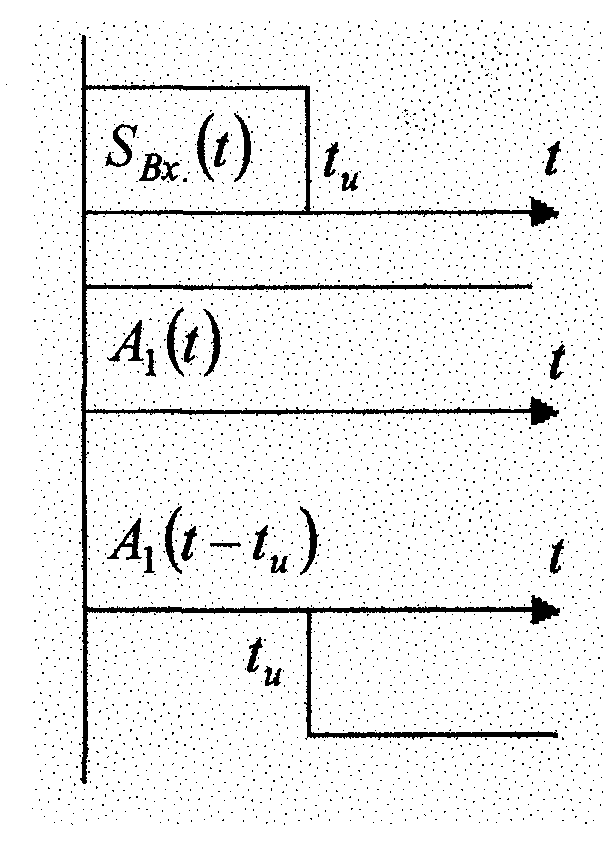 астосуємо розглянуті методи аналізу для визначення вихідної напруги у RC- колі , якщо на вході діє прямокутний імпульс. Прямокутний імпульс можна представити у виді різниці двох однакових стрибків, зміщених у часі на величину t₀ (див. рис .1.4)

Рисунок 1.4 - Представлення прямокутного імпульсу через різницю стрибків

тобто , де А₁ - амплітуда імпульсу (величина стрибка напруги); t_u - тривалість імпульсу. Тоді напруга на опорі легко знаходиться через перехідну характеристику h(t) .

Для даного кола , тоді

Такий же результат вийде і при аналізі спектральним методом. Легко можна знайти і напругу на ємності.

Форма сигналів на елементах кола залежить від співвідношення постійної часу кола RC = τ₀ тривалості імпульсу t_u. Для випадку τ₀ << t_u і τ₀ >> t_u графіки сигналів R і C побудовані на рис.1.5а та 1.5б відповідно. Аналогічні розрахунки можна провести і для RL- кіл.

Кола RC і RL при відповідному знятті вихідної напруги і визначених умов застосовуються для одержання сигналу, приблизно пропорційного похідної від вхідного сигналу, тобто як диференціальні кола (рис. 1.5а) чи для одержання сигналу, пропорційного інтегралу вхідного сигналу, тобто як інтегрувальні кола (рис.1. 5б).

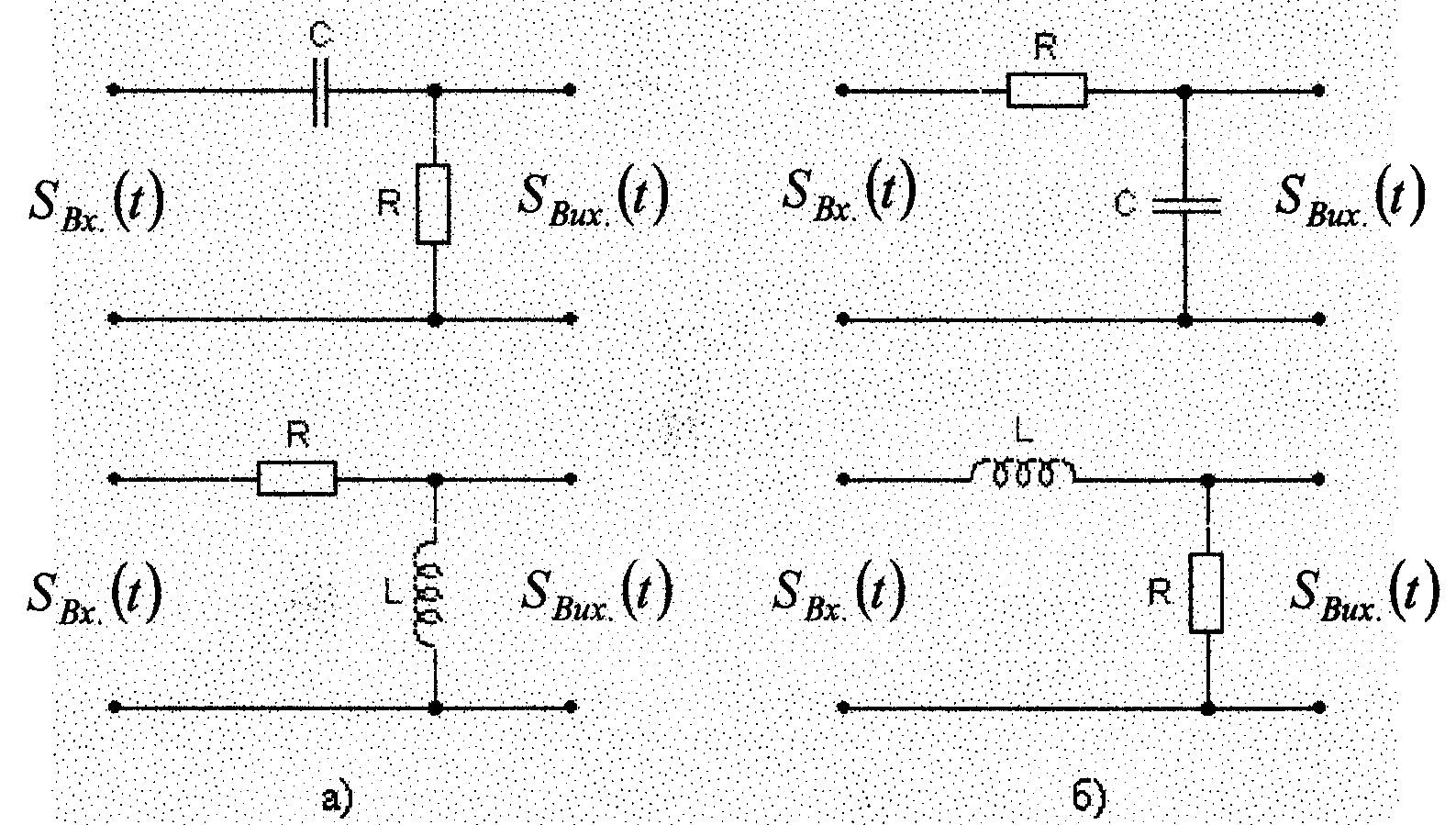
Рисунок 1.5 – Принципові схеми-електричні диференціальних

та інтегрувальних кіл

Для RC- кола запишемо за законом Кирхофа

Нехай напруга знімається з R і RC = ₀ << t_u. У момент t = 0 напруга на ємності дорівнює нулю, і вся напруга прикладена до опору. По закінченні перехідного процесу (3-5)τ₀ при нашій умові конденсатор зарядиться майже до повної вхідної напруги Напруга на опорі стане рівною

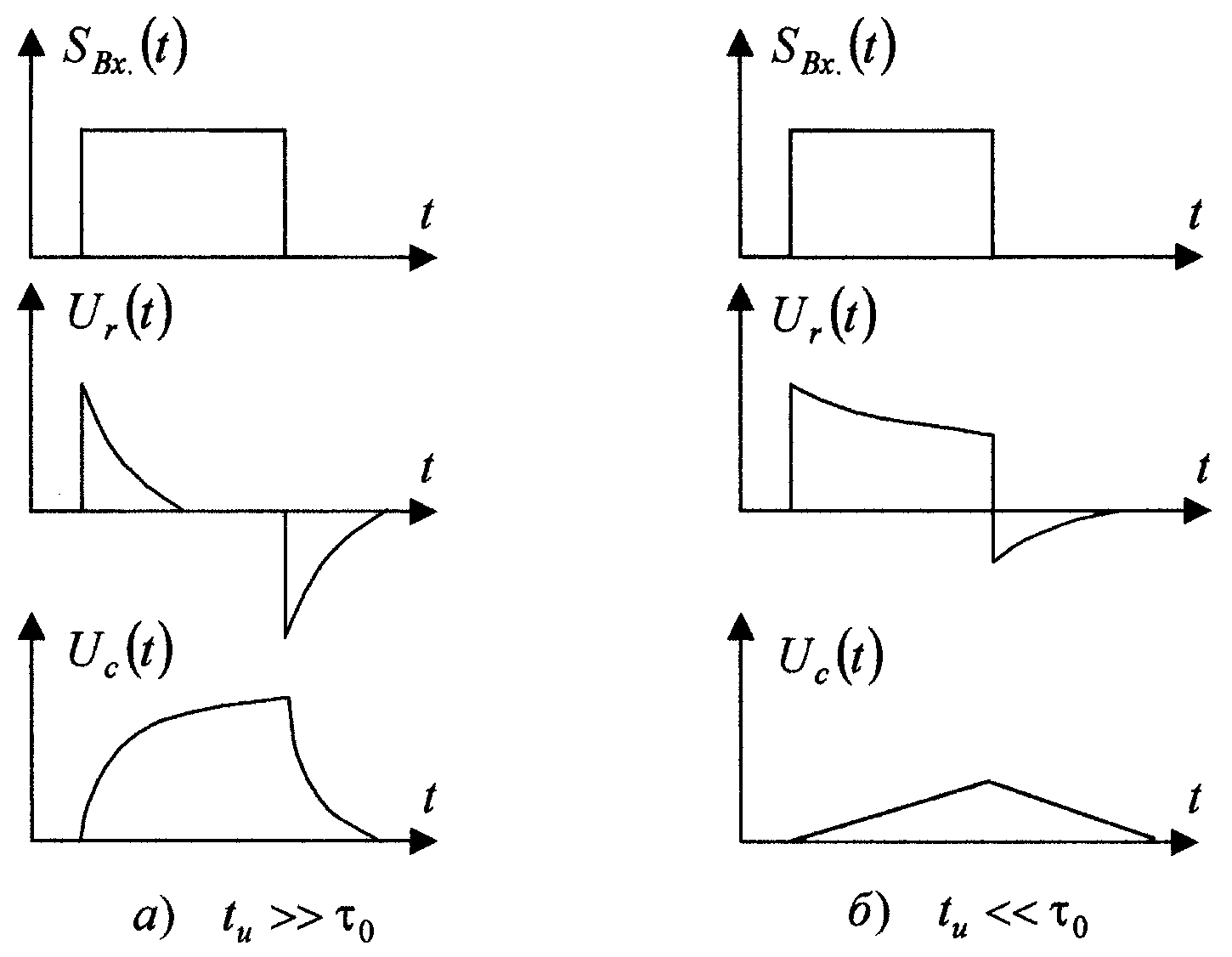
Рисунок 1.6 - Форма сигналів на виходах диференціальних та інтегрувальних кіл

Отже, на виході кола, що диференціює, при τ₀ << t_u i буде сигнал у формі коротких імпульсів (див рис.1.6а). Чим менше τ₀ в порівнянні з тривалістю імпульсу t_u тим краще диференціювання. В ідеальному випадку вихідний сигнал являє собою два δ - імпульси. Умову задовільного диференціювання можна одержати з спектральної точки зору. Вона записується у вигляді Ωτ₀ << 1. Ця умова повинна виконуватись для всіх частот головної частини спектра. Якщо головна частина спектра прямокутного імпульсу містить частоти в смузі [ 0-2π/t_i ], то умова запишеться: , або τ₀ << t_u. Отже, чим довший імпульс (нижче частоти головної частини спектра) тим краще він диференціюється при тієї ж τ₀.

Кола (рис.1.5б) при виконанні умови τ₀ >> t_u застосовуються для інтегрування сигналів. На виході їх можна одержати напругу

У цьому випадку на ємності до моменту закінчення імпульсу перехідний процес не встигає закінчитися, і напруга на ній наростає лише до малої величини (рис.1.6б).

З частотної точки зору умова задовільного інтегрування запишеться як , тобто при тій же τ₀ краще інтегрується короткий імпульс.

Кола RC і RL взаємозамінні, тому що струм в індуктивності під час перехідного процесу змінюється за тим законом, що і напруга на ємності.