Министерство образования и науки Российской Федерации

Филиал федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

Уфимский государственный нефтяной технический университет

Филиал ФГБОУ ВПО УГНТУ в г. Салавате

Кафедра "Общенаучные дисциплины"

СОГЛАСОВАНО УТВЕРЖДАЮ

Зав. кафедрой ОНД Зам. директора по учебной работе, профессор

______________ А.К.Боровиков Ф.. М. Хазиев

________________________2011 ____________________________2011

Методические указания к лабораторной работе изучение электрических колебаний в связанных контурах

Дисциплина «Физика»

СОГЛАСОВАНО РАЗРАБОТАЛ

Инженер по охране труда ст. преподаватель кафедры ОНД

_____________ Г. В. Мангуткина ______________В.Г. Прачкин

____________________ 2011 ___________________2011

Салават 2011

Методические указания предназначены для специальностей 140610 «Электрооборудование и электрохозяйство предприятий, организаций и учреждений», 240801 «Машины и аппараты химических производств», 240403 «Химическая технология природных энергоносителей и углеродных материалов», 220301 «Автоматизация технологических процессов и производств», всех форм обучения.

Рассмотрено на заседании кафедры ОНД

Протокол №__________ от_____________2011

© Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Уфимский государственный нефтяной технический университет» в г. Салавате

ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ В СВЯЗАННЫХ КОНТУРАХ

ЦЕЛЬ РАБОТЫ: изучение обмена энергии в системе электрических контуров, слабо связанных между собой.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: компьютер в сборе, плата L-140, модуль ФПЭ-13м, провода соединяющие.

Общие сведения

Колебательные процессы (осцилляции) в электрических контурах имеют аналогии в механике. Поведение простейшего осциллятора - одиночного маятника, представляющего собой массу, подвешенную на длинном стержне, хорошо изучено: это гармонические колебания с частотой ω₀.

Существенно более сложную структуру при колебаниях представляет собой система двух одинаковых маятников, связанных между собой слабой пружиной, как это показано на рис.1.

Маятники будут участвовать в коллективных колебаниях, амплитудно-частотная характеристика которых зависит от фазы смещения маятников друг относительно друга (относительная фаза).

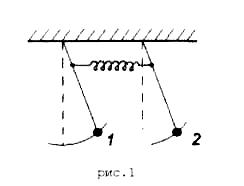
Рисунок 1

Если оба маятника имеют вначале (при t = 0) равные смещения, то они будут колебаться как единое целое с постоянной амплитудой и частотой, равными частоте и амплитуде колебаний одиночного маятника ω₀. Если при t=0 имеются равные и противоположные амплитуды, то маятники будут колебаться с постоянной амплитудой, но с некоторой другой, слегка повышенной по отношению к ω₀, частотой ω₁. Эти два вида движения называются нормальными модами колебаний системы связанных осцилляторов, причем вид колебаний с частотой ω₀ называют четной модой нормальных колебаний и обозначают знаком «+» (ω⁺=ω₀), а вид колебаний с повышенной частотой ω₁ называют нечетной модой нормальных колебаний и обозначают знаком "-". Нормальная мода колебаний - это коллективное колебание, при котором амплитуда колебаний каждой движущейся частицы системы остается неизменной. В более сложных случаях, когда при t= 0,имеется относительный сдвиг фаз, результирующее движение можно рассматривать как комбинацию (суперпозицию) двух нормальных мод колебаний, как амплитудно-модулированное колебание. С суперпозицией гармонических колебаний разных частот приходится встречаться в самых разнообразных явлениях. Примером могут служить не только маятники, но и два звучащих камертона с разными собственными частотами, причем наиболее интересным образом проявляется "смесовая" природа коллективных колебаний, когда частоты колебаний камертонов отличаются мало друг от друга. В этом случае человеческое ухо наиболее явственно воспринимает результирующее колебание как гармоническое колебание с переменной амплитудой, т.е. ухо слышит музыкальный тон, интенсивность которого периодически меняется с частотой и периодом . Такой вид суперпозиции гармонических колебаний, при ω₁≈ω₀ но и ω₁ >ω₀, иллюстрирует рис.2. Само это явление называется биениями ,а величины ω₆ и Т₆ – периодом и частотой биений соответственно.

Рисунок 2

В системе двух связанных слабой пружиной маятников биения могут установиться, если сместить один из них (например, маятник 1, слева рис.1), удерживая другой на месте, а затем отпустить их одновременно. В этом случае маятник 1 начинает колебаться один, но с течением времени колебания маятника 2 будут постоянно нарастать, а колебания маятника 1 - затухать. Через некоторое время маятник 2 испытывает сильные колебания, а маятник 1 останавливается. В случае четной моды нормальных колебаний, маятники движутся вместе, пружина не растянута и частота маятника такая же, как у одиночного маятника. В случае нечетной моды колебаний пружина растянута, что увеличивает частоту этой моды колебании. Если в какой-то момент времени смещен только один из маятников, то возникают две нормальные моды колебаний, находящиеся в определенной относительной фазе. Но поскольку частота нечетного колебания немного выше частоты четного колебания, относительная фаза изменяется в процессе коллективного колебания. Амплитуда колебаний первого маятника оказывается равной нулю, а амплитуда второго достигает максимума, когда два нормальных вида колебаний окажутся в противофазе, затем начнется увеличение амплитуды первого маятника и т.д

Поведение связанных осцилляторов легко объяснить с энергетической точки зрения: при t = 0 вся энергия сосредоточена в маятнике 1. В результате связи через пружину энергия постепенно передается от маятника 1 к маятнику 2 до тех пор, пока вся энергия не скопится в маятнике 2, затем, конечно, если система осцилляторов подпитывается извне энергией для компенсации затухания из-за трения и т.д., процесс обмена энергией повторяется от маятника 2 к маятнику 1 и т.д. Таким образом, "биения" - процесс обмена энергией между двумя гармоническими осцилляторами, собственные частоты которых различаются мало, а при t = 0 наблюдается относительный сдвиг фаз. Биения можно наблюдать и в электрической системе - в двух одинаковых LC -контурах, связанных между собой слабой емкостной связью Cf -аналог механической связи в виде пружины. Колебания в контурах (рис.3) возбуждаются с помощью преобразователя импульсов (ПИ).

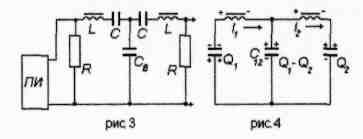
Рисунок 3 Рисунок 4

Для теоретических расчетов рассмотрены упрощенный вариант этой схемы (рис.4), где обозначены знаки зарядов в контурах и положительное направление тока: С_В=С₁₂, L₁=L₂=L. Причем для наблюдения биений важно, чтобы токи I₁ и I₂ были сонаправлены. Для двух контуров, соединенных по схеме рис.4, можно записать два уравнения, описывающих колебания зарядов Q в контурах:

(1)

Подставляя получаем:

(2)

Получились довольно сложные уравнения для двух переменных. Можно упростить ситуацию, написав новые уравнения, полученные сложением и вычитанием уравнений (2). Сложив эти уравнения получаем:

(3)

а разность этих уравнений дает

(4)

С помощью проведенных математических операций удалось уравнения (2) записать через переменные (Q₁+Q₂) и (Q₁-Q₂). Если при t=0 переменная (Q₁+Q₂) имеет значение (Q₁+Q₂)₀, то решение уравнения (3) имеет вид

(Q₁+Q₂)= (Q₁+Q₂)₀ cosω⁺t (5)

Частота равна частоте собственных колебаний отдельного контура. Аналогично, решение (4) приобретает вид

(Q₁ – Q₂) = (Q₁ - Q₂)₀ cosω^- t (6)

где ω ^- = , (Q₁ – Q₂)₀ – значения при t=0 переменная (Q₁ – Q₂).

Два вида движения, описываемые уравнениями типа (5) и (6), называются нормальными модами колебаний системы связанных осцилляторов. В данном случае они описывают колебания тока в системе двух связанных электрических контуров. Нормальная мода колебаний - это коллективное колебание тока, при котором амплитуда колебаний каждого заряда остается неизменной.

Если сместить из положения равновесия один из контуров, то результирующим колебанием явится колебание двух нормальных мод колебаний. При Q₂₀=0 из (5) и (6) получаем:

(7)

(8)

Используя известные тригонометрические тождества:

Можно записать уравнения (7) и (8) в виде:

(9)

(10)

Графики Q₁ и Q₂ (уравнения (9) и (10)) показаны на рис.2. Обратите внимание, что при t= 0 амплитуда Q₂ равна нулю. Амплитуда Q₂ увеличивается, а амплитуда Q₁ падает до тех пор, пока в момент времени, определенный из соотношения амплитуда Q₁, не станет равной нулю, а амплитуда Q₂ достигнет максимума.

При t=0 вся энергия сосредоточена в контуре 1. В результате связи через емкость С₁₂ энергия постоянно передается от контура 1 к контуру 2 до тех пор, пока вся энергия не соберется в контуре 2. Время, необходимое для перехода энергии из контура 1 в контур 2 и обратно, можно получить из уравнения , а частота, с которой контуры обмениваются энергией.

(11)

Для четной моды колебаний, обозначенной знаком "+", токи текут в одинаковом направлении , тогда на емкости С₁₂ нет заряда. При этом частота остается такой же, как для несвязанных контуров, т.е. . В случае нечетной моды нормальных колебаний (знак "-"), емкость С₁₂ заряжена, что увеличивает частоту колебаний, т.е. Следует отметить, что для того чтобы применить к связанным контурам рассмотренную выше теорию, они должны иметь одинаковую резонансную частоту и, кроме того, предполагается, что С₁₂ велика по сравнению с С ("слабая связь"). Тогда выражение (11) можно преобразовать следующим образом:

(12)

Полученное значение частоты обмена ω_обм (имеется в виду обмен энергии), или частота "биений" ω_обм=ω_биен можно изменять, настраивая систему контуров путем изменения номиналов радиоэлементов, добиваясь того, чтобы разностная частота (11) была сведена к минимуму.

Исследование биений, т.е. обмена энергий в связанных контурах, и является одной из практических задач данной работы.