3.4. Неустойчивость шнура с распределённым током

В реальных токамаках ток распределен по радиусу. Поэтому перейдем к рассмотрению устойчивости плазмы с распределённым током. Воспользуемся для анализа вариационным принципом (2.2.16). Для удобства приведем его снова:

Напомним, что все равновесные величины зависят только от радиуса , .

Для устойчивости функционал должен быть неотрицательным. Покажем, что первый и третий члены в сумме всегда неотрицательны. Для того чтобы вычислить работу плазмы при возмущении, умножим возмущенное давление (3.1.30) на :

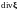. (3.4.1)

Пусть плазма сжалась, , а давление увеличилось, . При этом работа , совершённая внешней силой над плазмой, положительна, то есть . В случае расширения плазмы , 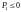, а величина по-прежнему. Таким образом, первый и третий члены в выражении (2.2.16) в сумме неотрицательны. Поэтому наиболее опасными являются несжимаемые возмущения, для которых .

Два последних интеграла в выражении (2.2.16) обращаются в ноль, так как объём вакуума равен нулю, а смещение плазмы на твёрдой границе также зануляется.

Итак, функционал (2.2.16) значительно упрощается:

, (3.4.2)

где . Второй член в фигурных скобках преобразуется следующим образом:

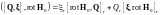. (3.4.3)

С учётом этого выражение (3.4.2) будет выглядеть как

. (3.4.4)

Компоненты вектора имеют вид:

; (3.4.5)

; (3.4.6)

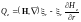. (3.4.7)

Вычислим теперь второй член в формуле (3.4.4).

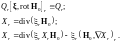(3.4.8)

Здесь . Окончательно получаем

(3.4.9)

Функционал теперь принимает вид

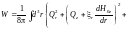
. (3.4.10)

Интеграл от дивергентного члена свёлся к интегралу по поверхности и выпал, так как смещение на жёсткой границе обращается в ноль.

Подставим в условие равновесия .

. (3.4.11)

В этом случае функционал принимает вид

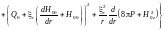. (3.4.12)

В интеграл входят только две независимые функции: и . Представим эти функции в виде гармоник:

(3.4.13)

Тогда компоненты вектора выразятся через и как

(3.4.14)

Интеграл (3.4.12) содержит члены, пропорциональные , 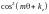и . При интегрировании члены вида и дают множитель , а члены, пропорциональные , зануляются. Постоянный множитель при минимизации функционала не важен, поэтому можно написать

(3.4.15)

Величина входит в функционал алгебраически. Поэтому его можно минимизировать, просто приравняв производную от подынтегрального выражения к нулю. Отсюда находим

. (3.4.16)

Подставим это выражение в (3.4.15)

(3.4.17)

Последний член можно проинтегрировать по частям, учитывая, что . В результате находим, что функционал представляется в виде

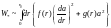. (3.4.18)

Здесь

;

.

Легко видеть, что задача свелась к принципу наименьшего действия в механике для одномерного движения материальной точки. Роль действия играет функционал . Уравнение, аналогичное уравнения Эйлера, имеет вид

. (3.4.19)

Очевидно, что наиболее опасными возмущениями являются те, для которых минимален первый член под интегралом в формуле (3.4.18), то есть

. (3.4.20)

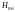Это винтовые возмущения, вытянутые вдоль силовой линии. Но и зависят от радиуса. Поэтому условие (3.4.20) может выполняться лишь на некоторых, так называемых резонансных поверхностях. Уравнения силовых линий на магнитной поверхности имеет вид . Здесь , – коэффициент запаса устойчивости. При целочисленном шаг силовой линии кратен периоду эквивалентного цилиндра. Вблизи резонансной силовой линии с шагом приближенно , где – отклонение от рациональной поверхности.

Рассмотрим наиболее простой случай . Функции и будут выглядеть так:

(3.4.21)

Два последних члена в g малы как x и x² и могут быть отброшены. Функционал W в этом случае упрощается:

. (3.4.22)

Здесь , штрих означает производную по r.

Уравнение Лагранжа для этого функционала имеет вид

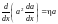, (3.4.23)

а его решение

,

где . Если , то – действительное отрицательное число, и оба решения расходятся в нуле. Если , одно из решений расходится в нуле, а второе нарастает к периферии, то есть не удовлетворяет граничному условию 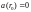. Это означает, что в обоих случаях возмущения не развиваются и плазма устойчива.

Пусть теперь . В этом случае решение, удовлетворяющее граничным условиям

,

сильно осциллирует в нуле, модель требует уточнения, и вопрос об устойчивости требует дальнейшего изучения.

В связи с этим рассмотрим модельную задачу. Введем безразмерную переменную , где – координата некоторой условной границы, достаточно далёкой от рациональной поверхности. Граничные условия будут иметь вид . Домножим функционал 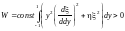на положительную величину :

. (3.4.24)

С помощью неравенства Буняковского

(3.4.25)

для первого члена в левой части неравенства (3.4.24) можно написать неравенство

. (3.4.26)

Мы проинтегрировали правую часть неравенства (3.4.24) по частям. Заменим первый член этого неравенства на меньший с помощью неравенства (3.4.26) и получим необходимое условие устойчивости:

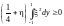, или , или . (3.4.27)

Здесь .

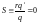Полученный критерий устойчивости называется критерием Сайдема. Заметим, что в системах для удержания плазмы . Поэтому при нулевом шире, , любой спадающий профиль неустойчив.