
- •Д.Х. Морозов Введение в теорию горячей плазмы
- •Часть 2
- •Оглавление
- •Глава 1. Равновесие плазмы в системах
- •Глава 2. Гидродинамический подход к описанию
- •Глава 3. Устойчивость идеальной плазмы
- •Глава 4. Резистивные неустойчивости 62
- •Глава 5.Элементы теории переноса тепла и частиц 75
- •Глава 6. Излучение плазмы 84
- •Глава 3 посвящена следующим неустойчивостям идеальной плазмы:
- •3. Неустойчивость на запертых частицах.
- •Глава 1. Равновесие плазмы в системах
- •1.1. Уравнение Шафранова–Грэда
- •1.2. Равновесие плазмы в токамаке
- •Глава 2. Гидродинамический подход
- •2.1. Метод малых возмущений
- •2.2. Энергетический принцип
- •Глава 3. Устойчивость идеальной плазмы
- •3.1. Желобковая неустойчивость
- •3.2. Неустойчивости цилиндрически симметричных
- •3.3. Винтовая неустойчивость
- •3.4. Неустойчивость шнура с распределённым током
- •3.5. Винтовая неустойчивость в системах типа «токамак»
- •3.6. Ионная температурно-дрейфовая неустойчивость.
- •3.7. Неустойчивость на запертых частицах
- •Глава 4. Резистивные неустойчивости
- •4.1. Тиринг-мода
- •4.2. Дрейфовая диссипативная неустойчивость
- •Глава 5. Элементы теории переноса тепла
- •5.1. Классическая теория переноса
- •5.2. Неоклассическая теория переноса
- •Глава 6. Излучение плазмы
- •6.1. Циклотронное и тормозное излучения
- •6. 2. Линейчатое и рекомбинационное излучения
- •6.3. Радиационно-конденсационная неустойчивость.
- •Часть 2
- •115409, Москва, Каширское шоссе, 31
- •144000, Московская область, г.Электросталь, ул.Красная, д.42
3.2. Неустойчивости цилиндрически симметричных
плазменных конфигураций
В этом разделе мы
рассмотрим неустойчивости идеальной
плазмы, то есть будем пренебрегать
диссипативными процессами. Такие
неустойчивости наиболее опасны.
Во-первых, они обычно занимают по радиусу
всю область плазменного шнура. Во-вторых,
время их нарастания чрезвычайно мало.
Действительно, оно по порядку величина
равно отношению радиуса плазменного
шнура a
к альфвеновской
скорости
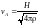 и в современных плазменных установках
составляет величину порядка 10-8
÷ 10-7
с.
и в современных плазменных установках
составляет величину порядка 10-8
÷ 10-7
с.
Рассмотрим вначале простейшую теорию неустойчивости цилиндрически симметричной конфигурации относительно цилиндрически симметричного возмущения, так называемой неустойчивости относительно перетяжек, или «сосисочной неустойчивости».
Пусть равновесная
конфигурация представляет собой
однородный плазменный цилиндр радиуса
a.
Пусть вдоль оси цилиндра, совпадающей
с осью z,
по поверхности
цилиндра протекает ток J.
Цилиндр помещен в продольное магнитное
поле
 внутри плазмы и
внутри плазмы и
 вне её. Вне цилиндра
вне её. Вне цилиндра
 существует полоидальное магнитное поле
существует полоидальное магнитное поле
 .
Пусть теперь на плазменном цилиндре
образовалась перетяжка, радиус которой
равен
.
Пусть теперь на плазменном цилиндре
образовалась перетяжка, радиус которой
равен
 (рис. 8).
(рис. 8).
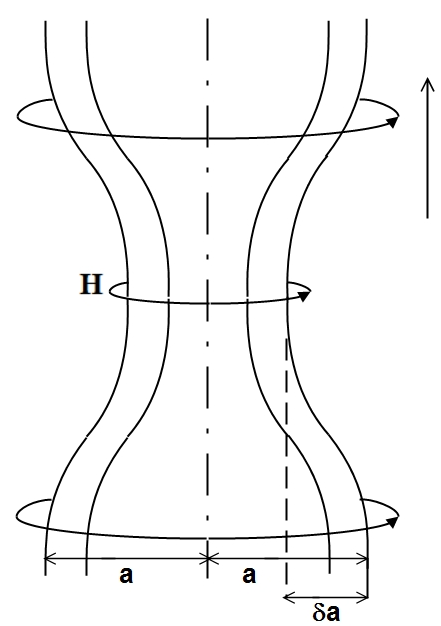
Рис. 8. Неустойчивость относительно перетяжек
В силу идеальной проводимости поток магнитного поля через сечение перетяжки должен сохраниться:
 .
(3.2.1)
.
(3.2.1)
Отсюда в первом приближении находим:
 .
(3.2.2)
.
(3.2.2)
Ток внутри шнура
остался прежним, поэтому и циркуляция
вектора
 также
сохранилась,
также
сохранилась,
 ,
то есть
,
то есть
 .
.
Вне плазмы магнитное
давление в первом по возмущению
приближении равно
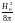 ,
а внутри –
,
а внутри –
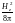 .
Газокинетическое давление сохранилось.
Поэтому равенство полных давлений по
обе стороны границы плазмы в линейном
приближении можно записать так:
.
Газокинетическое давление сохранилось.
Поэтому равенство полных давлений по
обе стороны границы плазмы в линейном
приближении можно записать так:
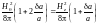 .
(3.2.3)
.
(3.2.3)
Если давление внутри плазмы при образовании перетяжки выросло, то есть
 ,
(3.2.4)
,
(3.2.4)
то плазма устойчива, если наоборот, то неустойчива, и перетяжка будет развиваться.
3.3. Винтовая неустойчивость
Более общим случаем возмущений цилиндрической плазменной конфигурации является винтовое возмущение. Идеальную винтовую моду в иностранной литературе называют «kink mode». Будем в этом разделе следовать монографии [3].
Для анализа таких возмущений вернемся к достаточно общему уравнению (2.1.31). Напомним, что это уравнение описывает идеальную плазму, то есть плазму с бесконечной проводимостью. Как и в предыдущем разделе, градиент давления и ток в плазме (за исключением тока по поверхности) равны нулю. Такое распределение тока имеет место в пинчах:
 (3.3.1)
(3.3.1)
Будем рассматривать несжимаемую плазму
 .
(3.3.2)
.
(3.3.2)
Тогда уравнение (2.1.31) существенно упрощается:
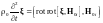 .
(3.3.3)
.
(3.3.3)
Ищем решение этого уравнения в виде
 .
(3.3.4)
.
(3.3.4)
Так как смещение зависит от радиуса-вектора, волновой вектор является оператором,
 . (3.3.5)
. (3.3.5)
Подставляя это выражение в (3.3.2) и учитывая, что , окончательно получаем
 .
(3.3.6)
.
(3.3.6)
Умножим это
уравнение скалярно на
 .
В силу (3.3.2) левая часть полученного
равенства обращается в ноль. Правая
часть обращается в ноль, если
.
В силу (3.3.2) левая часть полученного
равенства обращается в ноль. Правая
часть обращается в ноль, если
 . (3.3.7)
. (3.3.7)
Мы предположили,
что
 ,
где m
– целое число.
,
где m
– целое число.
Общим решением уравнения (3.3.7) является линейная комбинация модифицированной функции Бесселя и функции Кельвина:
 , (3.3.8)
, (3.3.8)
где С1
и С2
– произвольные постоянные. Функция Km
расходится в нуле, поэтому С1
= 0. Выражая
C2
через
 ,
имеем
,
имеем
 . (3.3.9)
. (3.3.9)
Подставим
 в радиальную компоненту уравнения
(3.3.6), имея в виду, что радиальная
составляющая волнового вектора является
оператором,
в радиальную компоненту уравнения
(3.3.6), имея в виду, что радиальная
составляющая волнового вектора является
оператором,
 .
.
 .
(3.3.10)1
.
(3.3.10)1
Штрих означает
производную по аргументу. Это решение
должно быть «сшито» с решением в вакуумной
области, где rotH
= 0.
Следовательно,
магнитное поле может быть представлено
как градиент некоторой функции
 .
Тогда уравнение divH = 0
переходит
в уравнение Лапласа, решение которого
снова имеет вид (3.3.8). Но во внешней
области
.
Тогда уравнение divH = 0
переходит
в уравнение Лапласа, решение которого
снова имеет вид (3.3.8). Но во внешней
области
 при
при
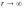 ,
поэтому С1
= 0.
В результате
,
поэтому С1
= 0.
В результате
 . (3.3.11)
. (3.3.11)
На границе плазмы
должно выполняться условие (2.1.38). При
условии несжимаемости
 оно приводится к виду
оно приводится к виду
 .
(3.3.12)
.
(3.3.12)
Из (2.1.27) находим
 , (3.3.13)
, (3.3.13)
а для возмущения поля во внешней области
 .
(3.3.14)
.
(3.3.14)
Подставляем эти выражения в (3.3.12):
 .
(3.3.15)
.
(3.3.15)
Еще одно краевое условие – это обращение в ноль на границе тангенциальной составляющей электрического поля в системе отсчета, движущейся вместе с плазмой,
 .
(3.3.16)
.
(3.3.16)
Берем
rot
от этого уравнения, учитываем, что в
линейном приближении
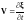 ,
и используем нормальную к границе
составляющую уравнения Максвелла
,
и используем нормальную к границе
составляющую уравнения Максвелла
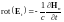 .
В результате получаем
.
В результате получаем
 .
(3.3.17)
.
(3.3.17)
Интегрируем это уравнение по времени:
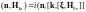 .
(3.3.18)
.
(3.3.18)
Учитывая, что
 ,
это равенство можно переписать следующим
образом:
,
это равенство можно переписать следующим
образом:
 .
(3.3.19)
.
(3.3.19)
Продифференцируем по радиусу (3.3.11) и подставим в левую часть этого равенства. Отсюда находим
 . (3.3.20)
. (3.3.20)
Подставляя (3.3.10) и (3.3.20) в (3.3.15), получаем в результате дисперсионное уравнение

 (3.3.21)
(3.3.21)
Неравенство
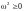 является критерием устойчивости системы.
Поскольку
является критерием устойчивости системы.
Поскольку
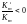 ,
второй член в правой части (так же, как
и первый) – стабилизирующий. Он имеет
минимум, если множитель
,
второй член в правой части (так же, как
и первый) – стабилизирующий. Он имеет
минимум, если множитель
 .
.
Пусть
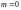 ,
,
 .
Условие устойчивости (3.3.21)
упрощается:
.
Условие устойчивости (3.3.21)
упрощается:
 .
(3.3.22)
.
(3.3.22)
Так как
 ,
мода заведомо устойчива, если
,
мода заведомо устойчива, если
 .
Этот случай соответствует перетяжкам
и уже был рассмотрен в разделе 3.2.
.
Этот случай соответствует перетяжкам
и уже был рассмотрен в разделе 3.2.
Мода
 ,
,
 – это винтовая мода, «змейки» в
русскоязычной литературе или «kink-mode»
в англоязычной. Рассмотрим эту моду в
пределе длинных волн,
– это винтовая мода, «змейки» в
русскоязычной литературе или «kink-mode»
в англоязычной. Рассмотрим эту моду в
пределе длинных волн,
 .
При этом для цилиндрических функций
можно использовать разложение в ряд:
.
При этом для цилиндрических функций
можно использовать разложение в ряд:
 ;
;
 .
.
При этом дисперсионное уравнение (3.3.21) принимает вид
 .
(3.3.23)
.
(3.3.23)
В рассмотренном
случае
 второй член в скобках отрицателен, и
плазма может быть неустойчивой.
второй член в скобках отрицателен, и
плазма может быть неустойчивой.
Рассмотрим типичный
для токамака случай
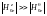 .
Снова будем исследовать предел
.
Разложим в ряд функции Бесселя и Кельвина:
.
Снова будем исследовать предел
.
Разложим в ряд функции Бесселя и Кельвина:
 ;
;
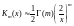 для
для
 .
.
Здесь
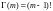 ;
;
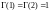 .
.
Дисперсионное уравнение (3.3.21) в этом приближении имеет вид
 .
(3.3.24)
.
(3.3.24)
Квадрат частоты
является квадратичной формой волнового
вектора
 (рис. 9).
(рис. 9).
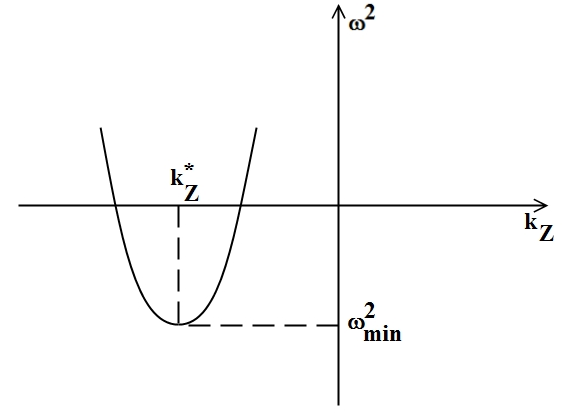
Рис. 9. Качественная зависимость квадрата частоты от kz
Значение
 ,
соответствующее
минимуму этой кривой, определяет
максимальный
инкремент.
Это достигается при значении
,
соответствующее
минимуму этой кривой, определяет
максимальный
инкремент.
Это достигается при значении
 ,
когда
парабола достигает минимума,
т. е.
,
когда
парабола достигает минимума,
т. е.
 .
(3.3.25)
.
(3.3.25)
Условие устойчивости имеет вид
 .
(3.3.26)
.
(3.3.26)
Выразим это условие
устойчивости через параметр
 .
.
Условие равновесия
при
 принимает вид
принимает вид
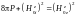 ,
что можно переписать так:
,
что можно переписать так:
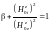 .
(3.3.27)
.
(3.3.27)
Выражая правую
часть неравенства (3.3.26) через
 ,
получаем условие устойчивости
,
получаем условие устойчивости
 ,
(3.3.28)
,
(3.3.28)
что в пределе
 дает
дает
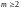 .
(3.3.29)
.
(3.3.29)
Это означает, что
моды
 и
и
 неустойчивы, остальные – устойчивы.
неустойчивы, остальные – устойчивы.
В реальных
тороидальных системах величина
 ограничена снизу,
ограничена снизу,
 ,
где
,
где
 и
и
 – длина окружности и большой радиус
тороидальной системы.
– длина окружности и большой радиус
тороидальной системы.
В бесконечном
цилиндре наиболее неустойчива мода с
.
В случае цилиндра с отождествленными
концами на
 налагается ограничение
налагается ограничение
 ,
и если
,
и если
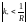 ,
то наиболее неустойчивой оказывается
мода с
,
то наиболее неустойчивой оказывается
мода с
 .
Для этого случая при
.
Для этого случая при
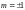 ,
условие
(3.3.24) можно переписать как
,
условие
(3.3.24) можно переписать как
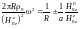 .
(3.3.30)
.
(3.3.30)
Плазма устойчива, если положительна правая часть этого равенства,
 .
.
Это условие называют
условием Крускала–Шафранова, а величину
 – коэффициентом запаса устойчивости
Шафранова.
– коэффициентом запаса устойчивости
Шафранова.
Данное условие
несколько модифицируется, если плазменный
цилиндр окружён бесконечно проводящей
стенкой при
 .
В этом случае дисперсионное уравнение
превращается в следующее:
.
В этом случае дисперсионное уравнение
превращается в следующее:
 . (3.3.31)
. (3.3.31)
При удалении бесконечно проводящей стенки на бесконечность дисперсионное уравнение переходит в уравнение (3.3.24). При приближении стенки к границе плазмы система становится устойчивой.
