Глава 3. Устойчивость идеальной плазмы

В СИСТЕМАХ С ЗАМКНУТЫМИ МАГНИТНЫМИ

ПОВЕРХНОСТЯМИ

В этой главе мы рассмотрим конкретные неустойчивости, характерные для плазменных конфигураций в термоядерных установках.

3.1. Желобковая неустойчивость

Одной из наиболее опасных оказывается так называемая желобковая (flute-like в зарубежной литературе) неустойчивость. Её ещё называют перестановочной или конвективной неустойчивостью. Эта неустойчивость весьма опасна, т.к. она практически не возмущает магнитного поля.

Рассмотрим эту неустойчивость в пробкотроне.

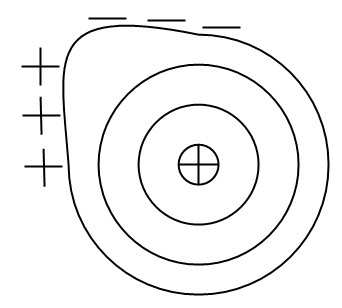
Рис. 4. Желобковое возмущение

Пусть трубка плазмы, вытянутая вдоль силовых линий, всплывает из более горячей и плотной области в менее плотную и более холодную. Сечение магнитных поверностей пробкотрона, перпендикулярное оси, показано на рис. 4. Это приводит к изгибанию линий постоянной плотности. Пусть магнитное поле направлено за плоскость чертежа. Если сечение проходит через середину пробкотрона, в этом сечении магнитное поле спадает к периферии. При этом положительно заряженные частицы дрейфуют в направлении вектора [H, H], то есть против часовой стрелки, а отрицательно заряженные – в противоположном направлении. В той области, где трубка «всплыла», на её краях выступят нескомпенсированные заряды и возникнет электрическое поле в полоидальном направлении. Под действием этого поля как положительно, так и отрицательно заряженные частицы будут испытывать ExВ-дрейф, приводящий к дальнейшему «всплыванию» частиц. Но частицы движутся также и вдоль силовых линий от пробки к пробке, попадая в те области вблизи пробок, где магнитное поле возрастает к периферии. В этих областях они будут дрейфовать к оси пробкотрона. В пробкотроне частицы плохо проникают в область пробок. В результате частицы в среднем будут смещаться наружу, то есть плазма будет неустойчива.

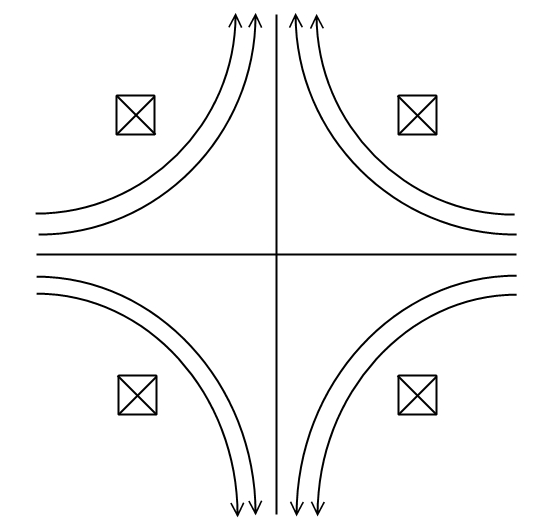
Рис. 5. Антипробкотрон

В антипробкотроне (см. рис. 5), когда поля от двух кольцевых токов направлены навстречу друг другу, магнитное поле всюду будет спадать по радиусу, и плазма будет устойчива. Но в экваториальном сечении в магнитном поле будет существовать круговая щель, через которую частицы будут быстро уходить из ловушки вдоль поля. Такая система для удержания плазмы непригодна.

Мы качественно рассмотрели желобковую неустойчивостью. Перейдем теперь к её количественному описанию.

Пусть силовая трубка, вытянутая вдоль силовых линий, «всплыла» из положения 1а–1б в положение 2а–2б (рис. 6), причём время «всплытия» много больше, чем время пролёта частиц между пробками.

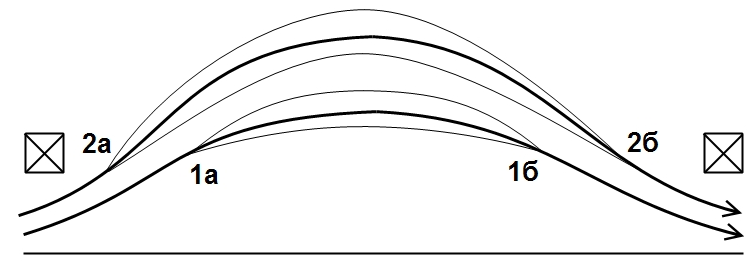
Рис. 6. Всплытие трубки в пробкотроне

Тогда при «всплытии» сохраняется продольный адиабатический инвариант . Выражая параллельную составляющую импульса через магнитный момент и полный импульс , получаем следующее выражение для адиабатического инварианта:

. (3.1.1)

Интегрирование здесь ведется между точками отражения. При смещении трубки из положения 1 в положение 2 меняются магнитное поле и точки отражения. При этом адиабатический инвариант не меняется:

. (3.1.2)

Найдем среднее за период изменение энергии частицы:

, (3.1.3)

а также вариацию магнитного поля . В установках типа токамак или стелларатор параметр , равный отношению плазменного давления к магнитному, мал, и возмущение магнитного поля можно считать практически вакуумным, то есть для него можно положить rotH = 0. Вычислим циркуляцию вектора Н по замкнутому контуру 1а–1б–2б–2а–1а, показанному на рис. 6. Будем считать контур узким, то есть интегралами на участках 1б–2б и 2а–1а можно пренебречь. Длина участка 1а–1б равна dl, магнитное поле на этом участке равно H. Длина участка 2а–2б равна , а магнитное поле, соответственно, равно . Таким образом, из условия обращения в ноль циркуляции магнитного поля получаем

. (3.1.4)

Если потенциальная энергия при отклонении от равновесия растёт, то система устойчива. Потенциальная энергия плазмы в трубке – это сумма энергий всех частиц в этой трубке. Вероятность пребывания частицы на отрезке силовой линии dl равна отношению времени пребывания на этом отрезке к времени пребывания между пробкам

Подставляя (3.1.4) в (3.1.3) и учитывая, что , получаем

. (3.1.5)

Вероятность пребывания частицы на отрезке равна отношению времени пребывания на нём к периоду обращения между пробками:

. (3.1.6)

Пусть в интервале на данной силовой линии содержится частиц. Тогда полное приращение энергии в трубке сечением dS имеет вид

(3.1.7)

Величина – это число частиц в фазовом объёме d³pd³r. Элемент объёма dV выражается через сечение трубки и элемент её длины, dV = dlsS. Величина HdS – это магнитный поток через площадку dS. При этом соотношение (3.1.7) перепишется так:

. (3.1.8)

В случае почти изотропной функции распределения можно написать:

. (3.1.9)

Среднеквадратичная скорость частиц в неподвижной плазме пропорциональна давлению:

. (3.1.10)

Плазма будет устойчива, если её энергия при отклонении от положения равновесия будет возрастать, , то есть

. (3.1.11)

Во многих реальных системах давление анизотропно. Простейшим примером такой системы является пробкотрон. Вследствие ухода через магнитные пробки распределение частиц по параллельным скоростям отличается от распределения по перпендикулярным. В декартовой системе координат тензор давления диагонален и имеет вид

, (3.1.12

где

; f – функция

_{распределения частиц по скоростям.}

_{В этом случае условие устойчивости (3.1.12) будет выглядеть так:}

. (3.1.13)

В токамаке продольное давление мало отличается от перпендикулярного . Согласно (1.1.5) должно выполняться равенство (H, P) = 0. Поэтому условие (2.1.11) переходит в условие

, (3.1.14)

С другой стороны, вариацию интеграла можно представить в следующем виде:

,

так как в замкнутых системах величина не варьируется. Таким образом, условие устойчивости имеет вид

. (3.1.15)

То есть интеграл должен убывать при удалении от оси системы.

Условие (3.1.15) можно представить несколько иначе:

, (3.1.16)

где – сечение трубки, – объём трубки, а – магнитный поток через это сечение. Условием устойчивости является убывание объёма силовой трубки с ростом заключённого в ней магнитного потока.

Очевидно, что невозможно создать систему с абсолютным минимумом магнитного потока. Но возможно создать систему с минимумом Н в среднем. Примерами таких систем являются цилиндр с эллиптическим сечением, в котором эллипс сечения вращается вокруг центральной оси, и пробкотрон со стабилизирующими стержнями (установка Иоффе, рис. 7).

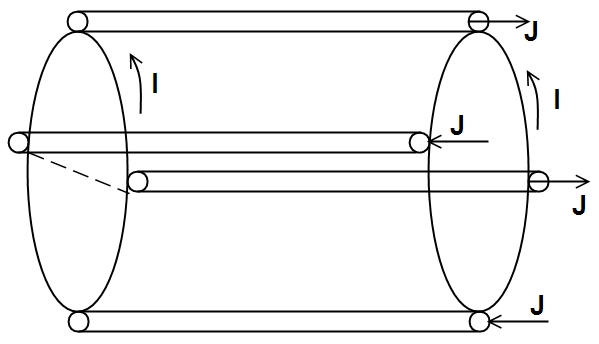
Рис. 7. Схема установки Иоффе

Подробнее об этом можно прочитать в работе [1].