1.2. Равновесие плазмы в токамаке

Ближе всего к параметрам термоядерного реактора в настоящее время находится токамак. Поэтому рассмотрим равновесие в такой системе подробно. Конфигурация его представляет собой тор с сильным продольным магнитным полем, вдоль которого течёт ток. В цилиндрическом приближении магнитные поверхности представляют собой коаксиальные цилиндры с постоянным радиусом. При свёртывании цилиндра в тор магнитные поверхности будут торами, оси которых будут смещены относительно магнитной оси. Рассмотрим такую тороидальную систему в приближении малой тороидальности. Отношение малого радиуса тора r к большому радиусу R обычно обозначают через . Будем рассматривать токамак в пределе малой тороидальности . Сечение магнитных поверхностей плоскостью в такой системе будет представлять систему вложенных слегка вытянутых окружностей со смещёнными центрами. Будем считать, что эти сечения мало отличаются от окружностей радиуса r.

Для описания магнитных поверхностей введём новую систему координат . Старые цилиндрические координаты будем называть 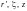. Удобно выбрать новую систему координат так, чтобы поверхности совпадали с магнитными поверхностями. Радиус поверхности будем называть малым радиусом в отличие от большого радиуса R, равного расстоянию от центра сечения данной поверхности до оси симметрии тора (рис. 3).

Пусть R₀ – большой радиус магнитной оси системы. Тогда центр магнитной поверхности радиуса r будет удален от оси симметрии тора на расстояние

. (1.2.1)

Рис. 3. Квазицилиндрическая система координат

Введем точку А на окружности . Радиус точки А в старой системе координат в новой системе координат выражается следующим образом:

. (1.2.2)

Угол показан на рис. 3. В случае малой тороидальности он мало отличается от азимутального угла . Тороидальное магнитное поле в этом случае можно представить как

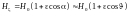. (1.2.3)

Азимутальное магнитное поле в том же приближении может быть представлено в виде

, (1.2.4)

где 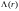– параметр асимметрии, зависящий от распределения тока и давления.

В новой цилиндрической системе координат квадрат элемента длины будет иметь вид

. (1.2.5)

Здесь – контравариантные компоненты вектора d l, g_ik – метрический тензор, отличные от нуля компоненты которого с точностью до имеют вид

; (1.2.6)

; (1.2.7)

; (1.2.8)

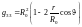. (1.2.9)

Уравнение силовых линий в ковариантном виде выглядит как

. (1.2.10)

Здесь

; (1.2.11)

. (1.2.12)

Величину удобно выразить так, чтобы силовые линии были прямыми, то есть выполнялось бы условие

. (1.2.13)

Для этого должно выполняться равенство

. (1.2.14)

Действительно, подставив это выражение в (1.2.11) и разделив на , находим

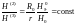. (1.2.15)

Из условия

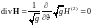, (1.2.16)

где , находим

; (1.2.17)

. (1.2.18)

Окончательно для метрического тензора получаем

; (1.2.19)

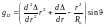; (1.2.20)

; (1.2.21)

. (1.2.22)

В этой системе координат, как уже указывалось, силовые линии являются прямыми и описываются выражениями

. (1.2.23)

Ковариантные и контравариантные компоненты магнитного поля имеют вид

; (1.1.24)

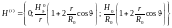. (1.2.25)

Составляющая будет содержать еще малую добавку к , возникающую из-за азимутального тока. В результате электрический ток выражается следующим образом:

. (1.2.26)

Подставляя ток в уравнение равновесия в нулевом по приближении получаем

. (1.2.27)

В следующем приближении имеем

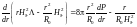, (1.2.28)

откуда простым интегрированием находим .

Здесь для простоты опущен индекс «0» у H и P.

Если положить, что на кожухе сдвиг обращается в ноль, можно написать

(1.2.29)

Эта величина называется смещением Шафранова.