6. 2. Линейчатое и рекомбинационное излучения

Несмотря на то, что концентрация примесей обычно не превышает нескольких процентов от концентрации основной плазмы, она может играть определяющую роль в энергобалансе и устойчивости благодаря тому, что линейчатое излучение не полностью ионизованной примеси оказывается весьма существенным.

Линейчатое излучение при плотностях плазмы, характерных для токамака и стелларатора, обычно можно рассчитать в корональном приближении. Для этого должны выполняться следующие условия:

а) характерное время ионизации наиболее представленного при данной температуре иона должно быть существенно больше времени жизни возбужденного состояния: ;

б) время между столкновениями электрона с ионом примеси должно быть много больше .

В данном приближении можно сначала вычислить распределение примесей по ионизационным состояниям, а затем просуммировать излучение от отдельных ионизационных состояний. При этом полагают, что излучение свободно выходит из плазмы. В таком приближении считается, что возможны только переходы между соседними ионизационными состояниями, то есть заряд иона может меняться только на единицу:

. (6.2.1)

Здесь 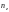– концентрация ионов с зарядовым номером ; и 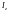– скорости рекомбинации и ионизации соответственно. Во всех приведенных ниже формулах для скоростей процессов температура и энергия ионизации измеряются в электрон-вольтах. При этом считается, что основным механизмом ионизации является ионизация электронным ударом. Скорость такой ионизации из основного состояния определяется выражением

cм³/c. (6.2.2)

Фотоионизацией в корональном приближении пренебрегают. В противоположном случае локального термодинамического равновесия (ЛТР) считается, что существует равновесие между процессами фотоионизации и фоторекомбинации, а для расчёта степени ионизации пользуются формулой Саха. Однако этот случай мы рассматривать не будем, так как в токамаках и стеллараторах эта ситуация реализуется крайне редко.

Рекомбинация в рассматриваемом нами случае может быть трёх типов: фоторекомбинация, трёхчастичная рекомбинация и диэлектронная рекомбинация. Для того чтобы одновременно выполнялись законы сохранения импульса и энергии, в процессе должны участвовать как минимум три частицы. В случае фоторекомбинации это ион, электрон и фотон. В случае трёхчастичной рекомбинации в процессе принимают участие два электрона и ион. Один из электронов захватывается ионом, а второй уносит избыток энергии, оставаясь свободным.

Диэлектронная рекомбинация происходит следующим образом. Сначала электрон захватывается в виртуальное состояние, в котором энергия связанного состояния превосходит энергию ионизации. Далее возможны два процесса. Первый – это когда захваченный электрон снова переводится в свободное состояние. Второй – если захваченный электрон остается захваченным, а избыток энергии высвечивается в результате каскада переходов электрона из возбужденного состояния в основное.

Скорость фоторекомбинации определяется в интервале 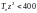эВ следующим приближенным выражением:

cм³/c. (6.2.3)

Скорость диэлектронной рекомбинации вычисляется по довольно сложному правилу и зависит от многих характеристик плазмы и примеси. Однако для лёгких примесей можно пользоваться приближенным выражением

(6.2.4)

Константы в этой формуле, зависящие от сорта примеси, приведены в работе [7]. Диэлектронную рекомбинацию, как правило, следует учитывать в термоядерной плазме.

Трёхчастичная (three body) рекомбинация в плазме токамака c лёгкими примесями играет существенную роль лишь при температурах не выше одного-двух эВ и описывается формулой

. (6.2.5)

Рекомбинационное излучение начинает играть определенную роль в том случае, когда линейчатое излучение уже довольно слабо, а тормозное ещё не слишком важно. Его интенсивность определяется выражением

. (6.2.6)

В стационарном случае (корональное равновесие) можно вычислить распределение примесей по её зарядовым состояниям, положив в уравнении (6.2.1) производную по времени равной нулю. Заметим, что в реальной плазме всегда существуют флуктуации, которые несколько смещают концентрации зарядовых состояний от их стационарных значений на величину, которая в предельном случае может составлять величину порядка тридцати процентов. Здесь мы, однако, не будем учитывать этот эффект.

В стационарном случае концентрация ионов с зарядом z зависит только от заряда и электронной температуры: . Величину можно вычислить аналитически, однако это имеет смысл лишь про малых z. В противном случае выражения получаются чрезвычайно громоздкими. Интенсивность излучения при этом сводится к произведению плотности электронов, суммарной плотности примеси

. (6.2.7)

Здесь , , – энергия перехода с уровня энергии иона j на уровень i, – частота таких переходов. Эта частота может быть вычислена по формуле

. (6.2.8)

Здесь i – исходный уровень, j – возбужденный уровень, – энергия перехода, – сила осциллятора, – гаунт-фактор, который зависит от отношения энергии перехода к температуре, атомного номера и изменения главного квантового при переходе. Очень грубая аппроксимация дает . Во многих случаях можно принимать во внимание только переходы в основное состояние. Тогда хорошая аппроксимация в области температур, типичных для токамака, 1 эВ < Т_е < 10 КэВ имеет вид

(6.2.9)

Результаты расчётов для излучения отдельных ионов и полного излучения примеси в корональном равновесии, отнесённого к одному иону примеси и к одному электрону (удельного), приведены на рис. 14 и 15.

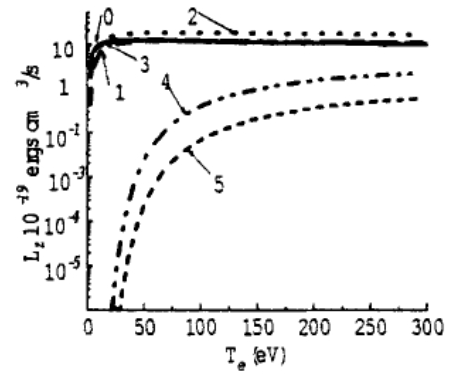
Рис. 14. Удельная мощность излучения иона с зарядом z

в зависимости от температуры

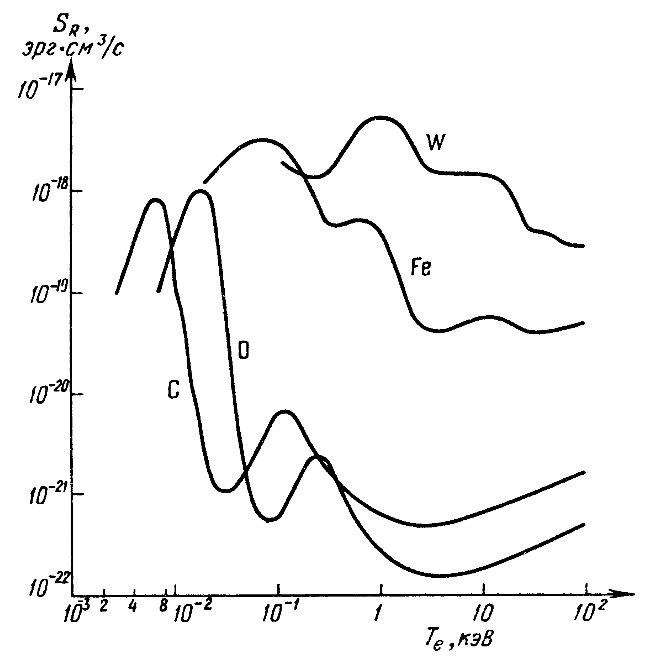
Рис. 15. Полное удельное излучение примеси для некоторых её видов

Подробные расчёты излучения примесей в корональном приближении приведены в работе [8].

Формулы (6.2.8) и (6.2.9) могут быть использованы и в нестационарном случае, если характерное время процесса много больше времени жизни возбужденного состояния. Это хорошо выполняется для радиационно-конденсационных неустойчивостей, которые будут рассмотрены ниже.

Отклонения от коронального приближения появляются, если:

1. время развития процесса меньше или порядка времени ионизации – рекомбинации, ;

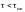2. плазма частично непрозрачна для собственного излучения, то есть длина пробега излучённого примесью фотона меньше размера плазмы, . Здесь – естественная ширина спектральной линии, а – внешняя ширина, возникающая, например, вследствие допплеровского уширения;

3. время девозбуждения электронным ударом порядка или меньше естественного времени жизни.

В этих случаях необходимо пользоваться радиационно-столкновительной моделью, хотя иногда хороший результат дают и поправки к корональной модели. В токамаке плазма может оказаться непрозрачной, если высока концентрация примесей и низка температура (например, при инжекции пеллет для подпитки реакции топливом, при срывах или инжекции нейтрального газа для смягчения последствий большого срыва).