Глава 5. Элементы теории переноса тепла

И ЧАСТИЦ

Проблема переноса тепла и частиц является одной из важнейших в проблеме термоядерного синтеза. Действительно, выход термоядерной энергии должен превосходить потери тепла. Это возможно лишь при достаточно высокой температуре, когда термоядерная реакция идет достаточно интенсивною. К сожалению, теория переноса в настоящее время далека от завершения. Эксперимент показывает, что потери тепла и частиц существенно превосходят те, что предсказывает классическая теория. При этом, если переносы по ионному каналу не слишком сильно отличаются от теоретических (так называемых неоклассических), то потери по электронному каналу обычно на порядок–два превышают неоклассические. Поэтому для расчётов термоядерных установок обычно пользуются эмпирическими скейлингами. В этой главе мы рассмотрим простейшую задачу переносов в прямом магнитном поле и так называемую неоклассическую теорию, базирующуюся на классических представлениях, но учитывающую особенности переносов в тороидальной геометрии.

5.1. Классическая теория переноса

В этом разделе мы рассмотрим классические, то есть не учитывающие тороидальных эффектов и турбулентности переносы в плазме. Уравнение непрерывности, описывающее переносы в направлении, перпендикулярном магнитным поверхностям, имеет вид

. (5.1.1)

Пока мы не конкретизировали вида перпендикулярной скорости отдельной частицы, такое уравнение описывает как классические переносы, так и аномальные. Будь то длина пробега в незамагниченной плазме, или ларморовский радиус в замагниченной, или расстояние, на которое частица переносится благодаря однократному взаимодействию с волной, если эта величина много меньше характерного размера задачи, например малого радиуса плазмы в токамаке, то такой перенос носит диффузионный характер. Поток плазмы, перпендикулярный магнитному полю, , пропорционален коэффициенту диффузии . В одномерном случае в отсутствие источников можно написать

. (5.1.2)

По порядку величины запишем

, (5.1.3)

где – длина пробега между столкновениями, а – время между ними. В спокойной замагниченной плазме для частиц сорта роль играет ларморовский радиус , а роль – обратная частота кулоновских столкновений частиц сорта с частицами сорта , и по порядку величины имеем

. (5.1.4)

Классический коэффициент диффузии можно более точно выразить через частоту столкновений. Для этого рассмотрим стационарное уравнение импульса для частиц сорта , сталкивающихся с частицами сорта :

. (5.1.5)

Здесь . Умножая это уравнение на векторно и раскрывая двойное векторное произведение, получаем

; (5.1.6)

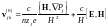. (5.1.7)

В первом приближении получаем

. (5.1.8)

Рассмотрим случай, когда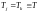

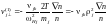. (5.1.9)

Поток частиц в направлении, перпендикулярном магнитному полю, пропорционален плотности и не зависит от сорта частиц

. (5.1.10)

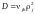Действительно, из третьего закона Ньютона , квадрат ларморовского радиуса пропорционален массе частицы, а коэффициент диффузии от неё не зависит. Таким образом, классическая диффузия автоматически амбиполярна, .