III. Домашнее задание: №197(2, 4); №201(2, 4); №206.
IV. Итог урока.
V. Дополнительное задание.
Практическая работа.
Постройте на одном чертеже графики функций: ,
,
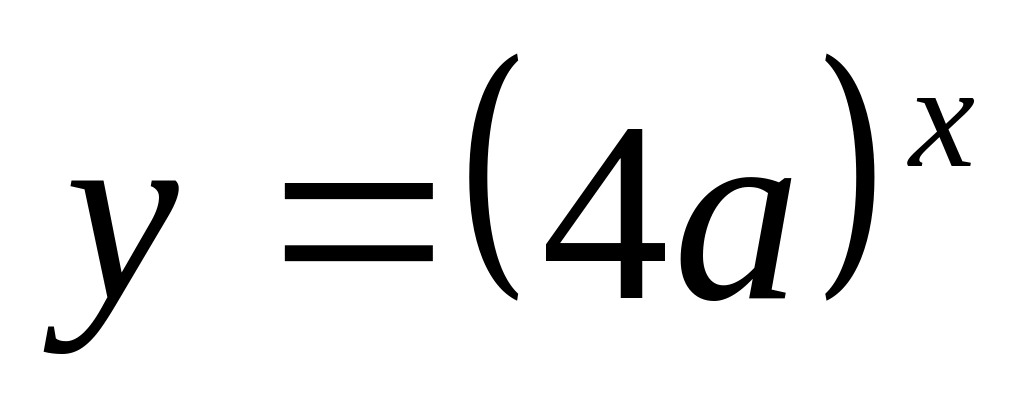.Найдите области значений каждой из этих функций на данном отрезке.
На каком отрезке надо задавать функцию: а) ; б) ;
в) , чтобы ее областью значений был данный отрезок ?
Вариант I |
Вариант II |
Вариант III |
Вариант IV |
|
|
б)
в)
|
1. а= 2. 3.
а) б) в) |
Ответ: Вариант I:
2.
;
;
.
Вариант II:
2.
;
;
.
Вариант III:
2.
;
;
.
3.
;
;
.
Вариант IV:
2.
;
;
.
3. ; ; .
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ.
Знания и навыки учащихся.
Знать вид показательных уравнений; знать алгоритмы решения показательных уравнений, уметь их решать, пользуясь алгоритмом.
Ур о к
I. Организационный момент.
II. Проверка знаний учащихся.
ДИКТАНТ
Вариант I [Вариант II]
Запишите функции:
;
;
;
;
.
Постройте схематично их графики.
Выпишите убывающие (возрастающие) функции.
Для каждой функции запишите множество значений.
Определите для каждой функции точку пересечения с осью ординат.
III. Изучение нового материала.
Показательное уравнение – это уравнение, в котором неизвестное содержится в показателе степени.
Решение уравнений.
Если показательное уравнение сводится к виду
(1)
Где а>0, a , то оно имеет единственный корень х=b.
Иногда, чтобы привести показательное уравнение к виду (1), необходимо в левой части уравнения вынести за скобки общий множитель
,
например:
,
и т.д.
Или разделить обе части уравнения на выражение, не равное нулю, например:
и т.д.
Некоторые показательные уравнения заменой
сводятся к квадратным. Надо помнить,
что t>0, так как показательная функция
не может принимать отрицательные
значения.Графическое решение уравнений сводится к построению графиков функций из левой и правой частей уравнения, отысканию по рисунку примерного значения абсциссы точки пересечения графиков. Если возможно, с помощью проверки уточняется корень уравнения.
№208 (1) – учитель показывает на доске решение:
.
№208(3) – на доске по желанию.
№208(2; 4) – самостоятельно по вариантам.
Ответ: 2)
3)
4)-
№209(1) – учитель с классом.
№209(3) – на доске по желанию.
Ответ: 1)- ; 3)-2.
№214 – самостоятельно по вариантам.
Ответ: 1)-4; 3; 2)5; 2; 3)3; 4)- .
№250(1; 3) – на доске по очереди.
Ответ: 1)1; 3)-1; 6.