Иррациональные неравенства
знания и навыки учащихся
Знать определение рационального неравенства, алгоритм решения этого неравенства; уметь решать иррациональные неравенства по алгоритму, а также с помощью графиков.
У р о к
I. Организационный момент.
II. Актуализация опорных знаний.
Решить уравнение:
а)
;
б)
2. Найти ОДЗ неравенства:
а)
;
б)
3. Укажите, какой функции:
а)
;
б)
;
в)
;
г)
соответствует график:
А. Б. В. Г.
III. Теоретическая часть.
Ввести определение иррационального неравенства.
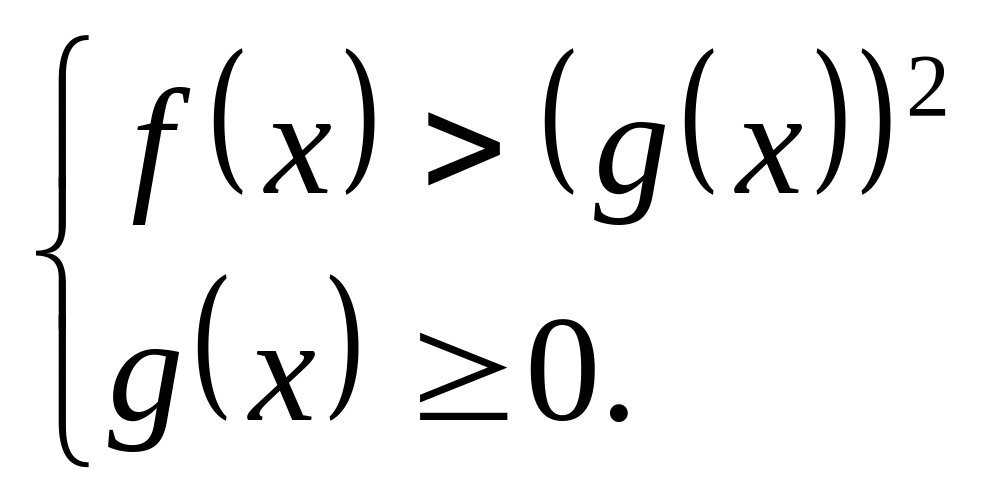
3.
4. Чтобы решить
неравенство
графически, нужно на одном рисунке
построить графики функций
и
и выяснить при каких значениях х точки
графика функции
лежат ниже точек графика функции
.
IV. Практическая часть.
№166(3,5, 6) – на доске по очереди.
Ответ: 3)х
;
5)х>
;
6)0
.
№167(1) – под диктовку.
№167(3) – за доской.
Ответ: 1)х>11;
3)-22<x
.
№170(1, 3) – на доске по желанию
№170(5) – учитель показывает на доске решение.
Д=1+8=9
,
Решение первой системы:
Решение второй системы:
Нет решений.
Ответ: -2<x<1.
№172(1) – учитель
показывает на доске решение:
Построим графики
функций
и
в одной системе координат.
График функции
лежит выше графика функции
при
Ответ:
№172(4) – на доске по желанию.
Ответ:
V. Домашнее задание: №166(2, 4); №167(2, 4); №170(4, 6); №172(2, 3).
VI. Итог урока. Объясните алгоритм решения иррационального неравенства.
У р о к
I. Организационный момент.
II. Проверочная работа (5-10 мин).
Решите неравенства.
Вариант I Вариант II
1)
1)
2)
2)
3)
3)
Ответ: В-I
1)0<x<1;
2)-5
;
3)
.
В-II 1)
;
2)
;
3)
.
III. Повторение.
Какая функция называется степенной?
Какой функции соответствует график?
а)
1)
2)
б)
в)
г)
д)
е)
3)
4)
ж)
5) 6) 7)
Ответ: а)-6; б)-5; в)-2; г)-1; д)-4; е)-3; ж)-7.
Изобразите схематически график функции и найдите ее область определения и область значений:
а)
;
б)
;
в)
;
г)
;
д)
.
4. Какая функция называется обратной? Какие функции являются взаимно обратными? Как найти функцию, обратную данной? Что вы можете сказать о графиках взаимно обратных функций?
№180(2, 3) – на доске по желанию.
№181 – самостоятельно по вариантам.
№185(1, 3) – под диктовку.
№186(1) – учитель с классом.
№186(2, 3, 4) – самостоятельно по вариантам.
Ответ: 1)
,
,
2)
;
,
3)
;
;
4)
,
,
5. Повторить алгоритм решения иррационального уравнения.
6. №187 – работа в парах (первая парта решает первое уравнение, вторая – второе и т.д.)
Ответ: 1)нет решений; 2)х=1; 3)нет решений; 4)х=0.
IV. Домашнее задание: №185(2), задание в рамочке Проверь себя».
V. Итог урока. Провести самоанализ знаний и навыков.
VI. Дополнительное задание.
1)
Решение.
ОДЗ уравнения:
или
х=2
или х=3
или
1+
не является корнем уравнения.
Ответ: 2; 3; 1- .
2)
Решение.
Ответ: 4.
3)
Решение.
Пусть
,
тогда
или
не является корнем.
,
т.е.
,
или
.
Ответ:т-1; 6.
У р о к
КОНТРОЛЬНАЯ РАБОТА
Цель: проверка знаний, умений и навыков учащихся по изученной теме.
Вариант I.
Найдите область определения функции:
а)
;
б)
2. Постройте график
функции
Найдите ее область определения и область
значений.
3. Найдите функцию,
обратную к данной, ее область определения
и область значений:
.
4. Решите уравнение:
а)
б)
5. Решите неравенство
Вариант II.
Найдите область определения функции
а)
б)
2. Постройте график
функции
Найдите ее область определения и область
значений.
3. Найдите функцию,
обратную к данной, ее область определения
и область значений:
4. Решите уравнение:
а)
б)
5. Решите неравенство
Ответы к контрольной работе.
Вариант I.
1.а)0
б)
2. Д
Е
3.Обратная функция
Д
Е
а) =
б)
Вариант II.
а)
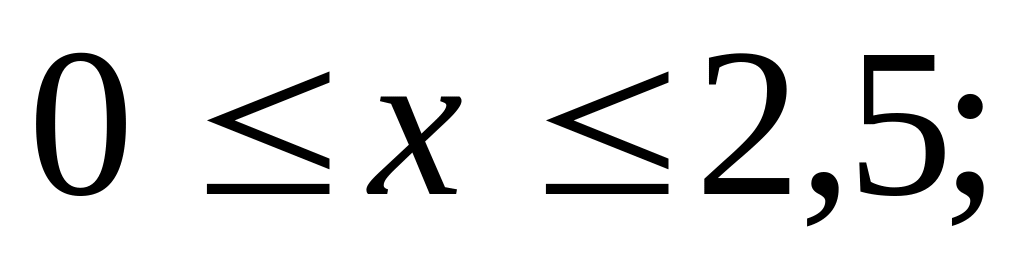б)
2. Д
Е
3.Обратная функция
Д
Е
а)
б)
5.
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА
И ГРАФИК
ЗНАНИЯ И НАВЫКИ УЧАЩИХСЯ
Знать определение показательной функции, три основных свойства показательной функции, уметь строить график показательной функции.
У р о к