
Алгебраические операции
Первоначальными понятиями в алгебре являются числа и действия над ними. В курсе арифметики и алгебры средней школы вводятся множества натуральных чисел – N;
целых чисел – Z; рациональных чисел – Q; иррациональных чисел; действительных чисел – R, а также четыре арифметических действия: сложение, вычитание, умножение и деление.
Напомним обозначения:
N={1,2,3,4,5,…} – множество натуральных чисел;
Z={…,-3,-2,-1,0,1,2,3,…} –множество целых чисел;
![]() - множество рациональных чисел.
- множество рациональных чисел.
Любое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби.
Множество R действительных (вещественных) чисел образовано числами, которые представимы в виде конечных или бесконечных десятичных дробей. Оно включает в себя перечисленные выше множества
![]() .
.
Для множества иррациональных чисел специального обозначения не вводят, так как это множество – есть разность R\Q. По определению это действительные числа, которые не являются рациональными.
Рассмотрим подробнее свойства арифметических операций. Каждая из арифметических операция производится над двумя числами, т.е имеет два операнда, а сама операция называется бинарной.
Для сложения и умножения чисел выполняются следующие свойства(законы):
сложение чисел коммутативно:
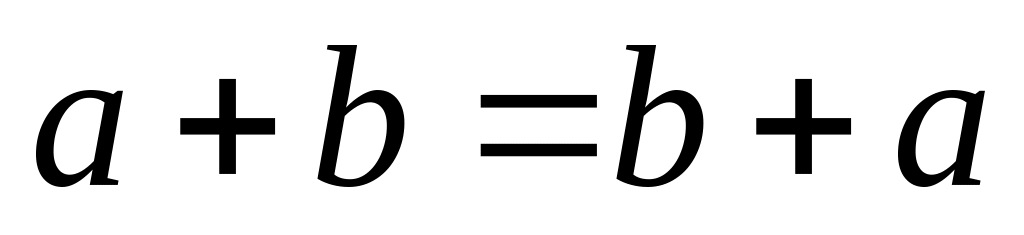 ;
;сложение чисел ассоциативно:
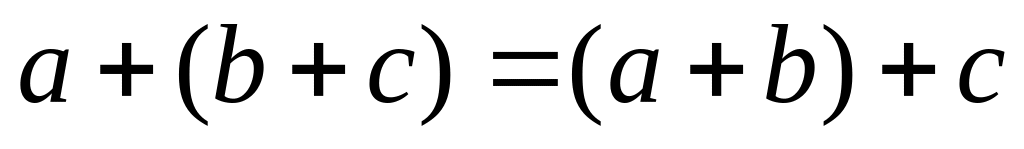 ;
;умножение чисел коммутативно:
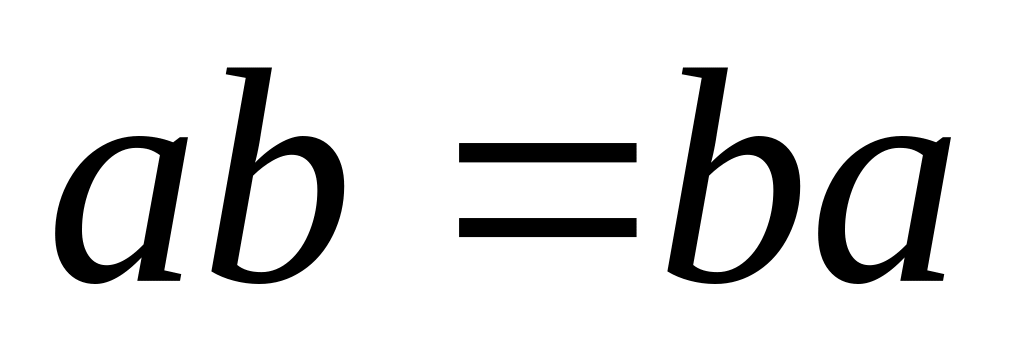 ;
;сложение чисел ассоциативно:
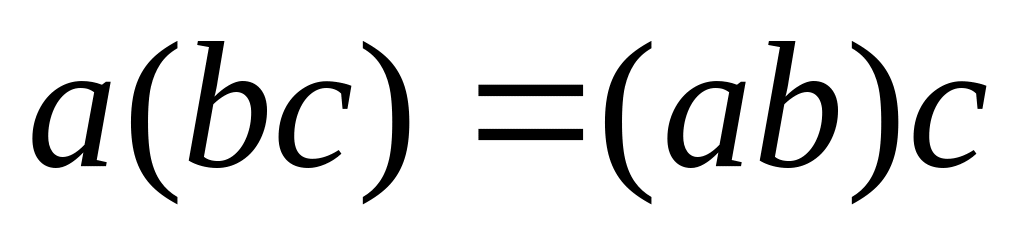 ;
;сложение и умножение связаны законом дистрибутивности:
 .
.
Вычитание и деление чисел вводятся как операции, обратные по отношению к сложению и умножению.
Разностью
![]() чисел a и b называют такое
число d, что
чисел a и b называют такое
число d, что
![]() .
.
Вычитание чисел можно определить (эквивалентным образом) по другому, подчеркивая особую роль числа нуль. В самом деле, число нуль обладает важным свойством: для любого числа а имеет место равенство а+0=а. Поэтому для любого числа а имеется противоположное число (-а) такое, что а+(-а)=0. Теперь разность а-b можно определить, как сумму числа а с числом, противоположным b:
![]() .
.
Аналогичным образом вводится операция
деления. Особую роль здесь играет число
1 (единица): для любого числа а
справедливо равенство
![]() .
Для любого числа а, отличного от
нуля, имеется обратное число
.
Для любого числа а, отличного от
нуля, имеется обратное число
![]() такое, что
такое, что
![]() .
Поэтому операцию деления чисел а
и b можно определить, как умножение
числа а на число, обратное к b:
.
Поэтому операцию деления чисел а
и b можно определить, как умножение
числа а на число, обратное к b:
![]() .
.
В отличие от сложения и умножения операции вычитания и деления чисел не удовлетворяют законам коммутативности и ассоциативности. Более того, если сложение и умножение двух любых натуральных чисел дает натуральное число, то при их вычитании или делении может получиться и не натуральное число. Поэтому говорят, что вычитание и деление не определены на множестве натуральных чисел (имея в виду, что они не выполняются для всех натуральных чисел). В этом смысле операция деления на отличное от нуля число не определена также и на множестве целых чисел.
Определим теперь понятие алгебраической операции, обобщающей арифметические действия. Пару чисел называют упорядоченной, если указано, какое число в этой паре является первым, а какое – вторым. Например, в упорядоченной паре (а,b) число а - первое, а число b – второе.
Определение 1. n-арной
операцией на множестве А называется
правило, по которому всякой упорядоченной
n-ке
![]() элементов из А поставлен в
соответствие некоторый единственный
элемент
элементов из А поставлен в
соответствие некоторый единственный
элемент
![]() .
.
Определение 2. Бинарной
операцией на множестве А называется
правило, по которому всякой упорядоченной
паре
![]() элементов из А поставлен в
соответствие некоторый единственный
элемент
элементов из А поставлен в
соответствие некоторый единственный
элемент
Будем говорить, что на множестве А
определена бинарная алгебраическая
операция (обозначим ее символом
![]() ),
если каждой упорядоченной паре паре
(а,b) элементов этого множества
ставится в соответствие элемент
),
если каждой упорядоченной паре паре
(а,b) элементов этого множества
ставится в соответствие элемент
![]() из этого же множества А.
из этого же множества А.
Задание бинарной операции на множестве
А равносильно заданию отображения
множества
![]() в множество А:
в множество А:
![]() .
.
Определим основные свойства (или законы) алгебраических операций.
Пусть на множестве А определена алгебраическая операция *. Говорят, что эта операция:
коммутативна, если
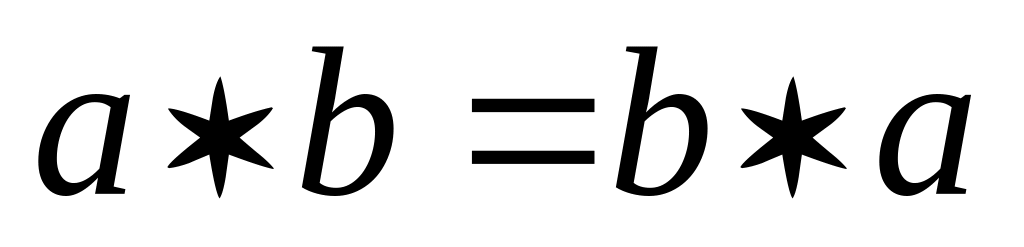
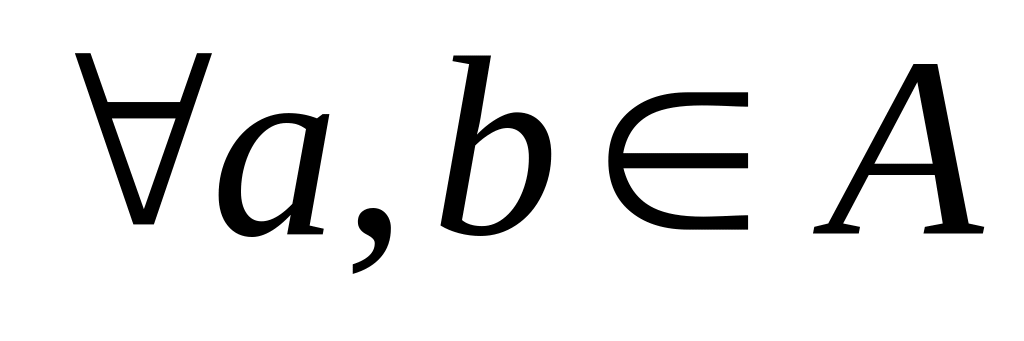 ;
;ассоциативна, если

 ;
;
Операции сложения и умножения подчиняются законам коммутативности ассоциативности на любом из множеств N, Z, Q, R.
Приведем примеры некоммутативных и неассоциативных операций.
Пример 3. Доказать, что
а) операция вычитания на множестве целых чисел не является коммутативной и ассоциативной;
б) операция «вычитания по модулю»:
![]() определенная на множестве целых чисел
является коммутативной, но не является
ассоциативной;
определенная на множестве целых чисел
является коммутативной, но не является
ассоциативной;
в) операция «умножения на модуль»:
![]() определенная на множестве целых чисел
не является коммутативной, но ассоциативна.
определенная на множестве целых чисел
не является коммутативной, но ассоциативна.
Решение.
а) Для опровержения какого-либо свойства достаточно привести контрпример:
![]() ;
- коммутативность;
;
- коммутативность;
![]() ;
- ассоциативность;
;
- ассоциативность;
б) для любых целых чисел а и b справедливо равенство
![]() - коммутативность;
- коммутативность;
Но эта операция не является ассоциативной, т.к.
![]() ;
;
в) для любых целых чисел а , b и с справедливо равенство
![]() - ассоциативность.
- ассоциативность.
Но эта операция не является коммутативной, так как это свойство не выполняется, например для чисел 1 и (-2):
![]() .
.
Для алгебраической операции можно определить обратную операцию.
Пусть на множестве А определена операция и выполняются два условия:
в А существует нейтральный элемент
 относительно операции * такой, что
относительно операции * такой, что
![]() ;
;
2)
![]() существует симметричный элемент
существует симметричный элемент
![]() такой, что
такой, что
![]() .
.
В аддитивной терминологии нейтральный
элемент называется нулевым и обозначается
символом
![]() ,
а в мультипликативной терминологии он
называется единичным и обозначается
символом
,
а в мультипликативной терминологии он
называется единичным и обозначается
символом
![]() .
.
В аддитивной терминологии симметричный
элемент
![]() называется
противоположным элементу
называется
противоположным элементу
![]() и обозначается символом
и обозначается символом
![]() ,
а в мультипликативной терминологии он
называется обратным к
и обозначается символом
,
а в мультипликативной терминологии он
называется обратным к
и обозначается символом
![]() .
.
Тогда для любой пары (а,b) можно
определить операцию
![]() ,
положив
,
положив
![]() .
.
В самом деле, элемент
![]() принадлежит А, поскольку
принадлежит А, поскольку
![]() ,
,
а операция
определена в А. Тем самым определена
операция
![]() ,
которую можно считать обратной по
отношению к операции
.
,
которую можно считать обратной по
отношению к операции
.
Покажем, что для сложения эти два условия
выполняются на множествах Z, Q, R,
поэтому на этих множествах определена
обратная операция – операция вычитания.
В самом деле, в каждом из множеств Z,
Q, R для операции сложения имеется
«нейтральный элемент» - нуль:
![]() для любого а. Кроме того, для любого
числа а существует «обратный
элемент» - противоположное число (-а):
для любого а. Кроме того, для любого
числа а существует «обратный
элемент» - противоположное число (-а):
![]() ,
причем противоположное число (-а)
принадлежит тому же множеству, что и
а. Осталось определить разность
чисел
,
причем противоположное число (-а)
принадлежит тому же множеству, что и
а. Осталось определить разность
чисел
![]() ,
как сумму числа а с числом,
противоположным числу b. Таким
образом условия 1) и 2) позволяют
определить операцию вычитания.
,
как сумму числа а с числом,
противоположным числу b. Таким
образом условия 1) и 2) позволяют
определить операцию вычитания.
Исследуем, на каких множествах можно
определить операцию деления. Сначала
рассмотрим множества Q, R. Операция
умножения, определенная на этих
множествах, удовлетворяет условиям 1)
и 2). Действительно, существует «нейтральный»
для операции умножения элемент –
единица:
![]() .
Кроме того, для каждого числа а,
отличного от нуля, существует «обратный
элемент» - число
.
Кроме того, для каждого числа а,
отличного от нуля, существует «обратный
элемент» - число
![]() :
:
![]() .
Следовательно, на множествах
.
Следовательно, на множествах
![]() можно определить частное
можно определить частное
![]() ,
как произведение числа а на число,
обратное к b, т.е. операцию деления,
обратную к умножению.
,
как произведение числа а на число,
обратное к b, т.е. операцию деления,
обратную к умножению.
Операция деления не определена на множествах N и Z.
Таким образом, вычитание определено на множествах Z, Q, R, а деление – на множествах .
