
- •Лекция 1. Составные высказывания. Основные понятия
- •Составные высказывания
- •Лекция 2. Основные логические операции. Формулы логики. Дизъюнктивная конъюнктивная нормальные формы. Логические операции.
- •Стрелка Пирса - ↓.
- •Формулы логики высказываний
- •Лекция 3. Изучение законов логики. Равносильные преобразования. Законы логики (свойства логических операций)
- •Логическое следствие
- •Лекция 4. Булевы функции.
- •Лекция 5. Совершенная дизъюнктивная и конъюнктивная нормальные формы (сднф и скнф)
- •Лекция 6. Понятие полноты множества функций. Замкнутые классы.
- •Лекция 7. Множества и подмножества.
- •Сравнение множеств.
- •Лекция 8. Операции над множествами
- •Свойства операций над множествами.
- •Лекция 9. Понятие предикат.
- •Лекция 10. Логические операции над предикатами. Операции над предикатами.
- •Кванторы.
- •Операции с кванторами.
- •Лекция 11. Понятие бинарного отношения и его свойства. Отношения.
- •Отношения на множестве.
- •Виды отношений:
- •Инъекция.
- •Сюръекция.
- •Биекция.
- •Лекция 12. Отношение эквивалентности.
- •Лекция 13. Композиция отображений Равенство соответствий
- •Произведение соответствий (композиция)
- •Композиция отображений. Ее свойства
- •Лекция 14. Операции над подстановками.
- •1: Коммутативность.
- •2: Ассоциативност ь.
- •3: Единица.
- •4: Обратный элемент.
- •Лекция 15. Понятие вычета по модулю n. Операции над вычетами. Шифрование.
- •Лекция 16. Метод математической индукции
- •Лекция 17. Генерирование к-элементных подмножеств данного множества
- •Размещения.
- •Формула числа размещений без повторений.
- •Другой вид формулы числа размещений.
- •Перестановки.
- •Свойства сочетаний.
- •Размещения с повторениями.
- •Задача о числе подмножеств данного множества.
- •Перестановки с повторениями.
- •Сочетания с повторениями.
- •Лекция 18. Понятие графа. Способы задания графа. Методика выделения компонента связности в графе
- •Смежность и инцидентность
- •Лекция 19. Изоморфные графы. Эйлеровы графы. Изоморфизм графов
- •Требования к представлению графов
- •Эйлеровы графы Вернемся к историческому примеру о Кенигсбергских мостах. В каком случае в графе можно найти цикл, в котором каждое ребро участвует ровно один раз?
- •Лекция 20. Плоские графы. Деревья и их свойства
- •Лекция 21. Понятие ориентированного графа
- •Орграфы и матрицы
- •Лекция 22. Сильносвязный орграф. Эйлеровы орграфы Ориентированные эйлеровы графы
- •Лекция 23. Базовые множества и принцип работы автоматов
- •Минимизация автоматов
- •Алгоритм минимизации автомата Мили
Лекция 23. Базовые множества и принцип работы автоматов
Автомат – дискретный преобразователь информации, который на основе входных сигналов, поступающих в дискретные моменты времени, и с учетом своего состояния вырабатывает выходные сигналы и изменяет свое состояние.
В данном разделе рассматриваются абстрактные автоматы, т.е. некоторая математическая модель. Вопросы практической реализации не рассматриваются. В связи с этим при построении автоматов будем иметь в виду, что:
Автомат функционирует в абстрактном времени.
Все переходы происходят мгновенно.
Автомат представляет собой кортеж 6 –го порядка:
![]() ,
,
где
![]() – множество входных сигналов (входной
алфавит),
– множество входных сигналов (входной
алфавит),
![]() – множество выходных сигналов (выходной
алфавит),
– множество выходных сигналов (выходной
алфавит),
![]() – множество внутренних состояний,
– множество внутренних состояний,
![]() – функция перехода,
– функция перехода,
![]() – функция выхода,
– функция выхода,
![]() - начальное состояние автомата.
- начальное состояние автомата.
Законы функционирования автоматов.
В зависимости от законов функционирования различают 3 вида автоматов:
Автоматы первого рода, или автоматы Мили:
![]()
Автоматы второго рода
![]()
Правильные автоматы второго рода, или автоматы Мура:
![]()
На практике наибольшее распространение получили автоматы Мили и автоматы Мура.
Задание автоматов
Автоматы могут быть заданы следующими способами:
В виде графа

Рис. 1. Автомат Мили
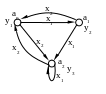
Рис.2. Автомат Мура.
При построении
автомата Мили каждая дуга, соединяющая
вершины
![]() и
и
![]() ,
имеет обозначение
,
имеет обозначение
![]() .
Это означает следующее: находясь, в
состоянии
.
Это означает следующее: находясь, в
состоянии
![]() автомат, отрабатывая входной сигнал
автомат, отрабатывая входной сигнал
![]() ,
выдает выходной сигнал
,
выдает выходной сигнал
![]() и переходит в состояние
и переходит в состояние
![]() .
.
Так как в автомате
Мура выходной сигнал
![]() зависит только от текущего состояния
,
то каждая дуга, соединяющая вершины
и
,
имеет обозначение
.
зависит только от текущего состояния
,
то каждая дуга, соединяющая вершины
и
,
имеет обозначение
.
В виде таблиц перехода и выхода (автомат Мили); отмеченной таблицы перехода (автомат Мура).
Автомат Мили описывается с помощью двух таблиц: таблицы перехода и таблицы выхода:
Таблица переходов (ТП) Таблица выходов (ТВ)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Автомат Мура описывается с помощью отмеченной таблицы перехода:
Таблица переходов (ТП)
Пример. Синтезировать автомат, на вход которого подаются монеты номинальной стоимостью 1, 2 и 3 копейки, а на выходе автомат выдает билет, если сумма набранных монет составляет 3 копейки, если сумма меньше 3 копеек, то автомат ничего не выдает, если сумма больше 3 копеек, то автомат возвращает деньги.
Определим входной, выходной алфавиты и множество внутренних состояний:
входной алфавит
 - монеты номинальной стоимостью 1, 2 и
3 копейки
- монеты номинальной стоимостью 1, 2 и
3 копейки
выходной алфавит
 - на выходе возможны выходные символы:
- на выходе возможны выходные символы:
 - ничего;
- ничего; - билет;
- билет; - возврат.
- возврат.множество внутренних состояний
 ,
,
где - начальное состояние автомата « в автомате ничего нет»;
- «в автомате 1 копейка»;
- «в автомате 1 копейка»;
- «в автомате 2 копейки»;
![]() - «в автомате 3
копейки».
- «в автомате 3
копейки».
Г раф
автомата имеет вид:
раф
автомата имеет вид:
Рис.3. Автомат Мили
Таблицы перехода и выхода представлены в виде:
Таблица переходов (ТП) Таблица выходов (ТВ)
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
Н |
Н |
Б |
Н |
2 |
|
|
|
|
|
2 |
Н |
Б |
В |
Н |
3 |
|
|
|
|
|
3 |
Б |
В |
В |
Б |
Неопределенным состоянием называется несуществующее состояние.
Частичным автоматом называется автомат, в котором некоторые состояния в таблице перехода не определены. Для дальнейшего исследования неопределенное состояние некоторым образом доопределяют.
