Лекция 14. Операции над подстановками.

Подстановка на множестве M – это биекция [7]:

M  N_n, n = |M|  N.

В случае конечного множества M (как выше) количество подстановок определяется как количество перестановок из n элементов:

Можно считать, n ящиков заполняются объектами x₁, …, x_n, x_i  M.

Поскольку M биективно N_n, можно определить подстановку как N_n  N_n, т.е. иметь дело только с натуральными числами:

{i₁, i₂, … , i_n} = N_n.

Обычно подстановка задается в форме стандартной таблицы, имеющей две строки. Верхняя строка всегда содержит последовательные натуральные числа, начиная с 1. В нижней строке, конечно, не должно быть повторений.

Например:

Подстановка, как и любое бинарное отношение, может быть составной

.

Видно, что в «контрпримере» , т.е. «произведение» подстановок некоммутативно.

В составе любой подстановки можно выделить циклы. Их длина может составлять 1, 2,…, n. Цикл длины 1 – это фактически вырожденный цикл, стационарный элемент.

Пример.

Здесь единственный цикл – типа RoL («Вращение влево»).

Пример.

Теорема.

Любая подстановка на конечном множестве A (т.е. биективному подмножеству N_n) может быть представлена как произведение непересекающихся циклов.

Действительно, начав слева, от 1 в верхней строке, формируем первый цикл по принципу «сверху вниз, снова вверх и т.д. до замыкания на начальное значение». На основе оставшихся элементов верхней строки формируем второй цикл и т.д. Поскольку множество А (или N_n) конечное, процесс рано или поздно останавливается.

Теперь нужно показать еще непересекаемость циклов. Это следует, например, из условия неповторяемости элементов (в нижней, например, строке рис. 1).

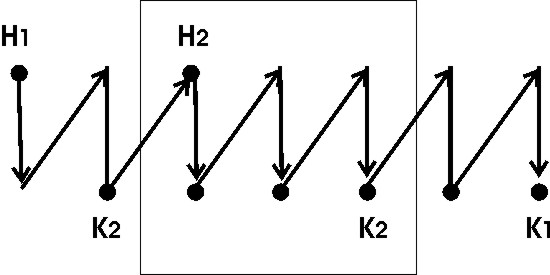
Рис. 1. К непересекаемости циклов

Доказательство от противного: пусть, наоборот, цикл 2 (H2, K2) вложен в цикл 1 (H1, K1). Тогда из-за обязательности равенств элементов на двойной стрелке (рис. 17) и K2 = H2 (замыкание) получаем в нижней строке запрещенное повторение элементов K2 .

На множестве М в отображении N  M можно определить последовательность. Например,

Функционал – это функция, определенная на множестве не простых объектов (чисел), а на множестве тоже, например, функций:

Здесь после стрелки указано множество, например, всех функций из M₂ в M₃ .

Пример.

тогда:

Можно считать функционал функцией с нетривиальной областью значений.

Еще один специальный случай связан с отображением, сохраняющим эквивалентность.

Пусть М – множество с -отношением эквивалентности. Тогда М разбивается этим отношением на -эквивалентные классы:

.

Итак, есть отношения эквивалентности _X и _Y определенные соответственно на множествах X и Y, и есть отображение . Есть еще межклассовые отношения:

Отображение f сохраняет эквивалентность, если f₁ – функция, т.е.

.

Если же f₁ – не функция, т.е. выходит за пределы класса эквивалентности (например, [х₁]), то f – не сохраняет эквивалентность.

В благоприятном же случае можно говорить: отображение f: X  Y индуцирует отображение (рис. 2).

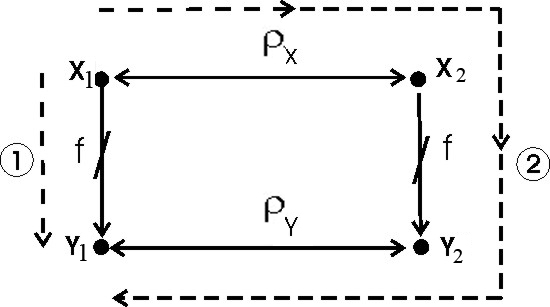
Рис. 2. Графическая интерпретация отображения f, сохраняющего эквивалентность

Видно, что существуют 2 пути от х₁ к y₁:

1: y₁ = f(x₁);

2: x₁_X x₂  y₂ = f(x₂)  y₂_Y y₁.

Пример.

X = {1, 2, 3}, Y = {1, 4, 9},

_X : X / _X = {{1}, {2, 3}},

_Y : Y / _Y ={{1},{4, 9}},

f: X  Y: x  x².

Здесь получаем:

f₁ ([1]) = [f(1)] = [1] = {1};

f₁ ([2]) = [f(2)] = [4] = {4, 9};

f₁ ([3]) = [f(3)] = [9] = {4, 9}.

Проверим f₁ на функциональность. Должно быть f₁ ([2]) = f₁ ([3]), но так и есть.

Пример.

Теперь

f₁  ([2]) = [f(2)] = [4] = {1,4};

f₁  ([3]) = [f(3)] = [9] = {9}  {1,4}.

Здесь f₁ – не функция, и замыкания двух путей нет (рис. 3).

Рис. 3. Отображение f, не сохраняющее эквивалентность

Операции

Операция над (на) множеством M это функция [7]:

Из определения операции видно, что она замкнута на множестве М, т.е. результат операции не выходит за пределы этого множества.

Еще одно свойство операции – однозначность результата, т.е.

упорядоченный набор n элементов (операндов) дает в результате операции только один элемент.

Порядок операции – это количество ее операндов: n = 1 соответствует унарной (монадической) операции, n = 2 – бинарной (диаедической) операции и т.д.

Далее рассматриваются только бинарные операции. Они могут быть заданы в одной из трех форм:

infix ( например, x + y);

prefix ( +xy );

postfix ( xy+ ).

Последние две формы дают бесскобочную запись (скобки вводятся, в инфиксной форме, для явного указания порядка выполнения операций).

Пример.

Инфиксная (обычная) форма:

a + b * c – (d – e / f).

Префиксная форма (проход и запись выражения справа налево):

+ a – * bc – d / e f.

Постфиксная форма (проход и запись слева направо), по-другому – это обратная (инверсная) польская запись (по имени польского математика Я. Лукасевича):

a b c * + d e f / – – .

Последняя форма (ОПЗ) широко используется в вычислительной технике, в частности при построении так называемых прямых трансляторов с языков программирования (используется стек с приоритетами).

Бинарная операция удобно задается таблицей (табл. 1).

Таблица 1

Операция на множестве M={a, b, c}

	a	b	c
a	a	a	b
b	b	a	c
c	a	b	b

В дальнейшем будем говорить о некоторых замечательных свойствах операций, связывая эти свойства с фиксированными номерами (1, 2, …).