Глава 6. Проектирование нечётких систем управления при помощи «fuzzy logic toolbox» для «Matlab»
Для анализа и синтеза систем управления, обладающих свойствами искусственного интеллекта, в среде Matlab используется специализированный пакет Fuzzy Logic Toolbox. Этот пакет позволяет синтезировать нечёткие логические регуляторы с использованием двух алгоритмов нечёткого вывода Мамдани и Сугено, а также осуществлять настройку таких регуляторов при помощи адаптивной нейронной сети. Ниже приведены основные приёмы работы с данным пакетом.
Использование команды fuzzy в командной строке основного окна Matlab запускает редактор нечётких структур FIS Editor (рис 6.1).
*-> ГІ5 Editor: Uni flit її
FF"
!■;
bri й
And
method
Ur
method
Aygregafiipn
nputl
Unfitted
ma
n
n
ач-
□вШШИЫИЮП
centre»
system milled" i input, i output, ага о ruées
untitled
(ffiaftdanQ
FIS Type
Current Venable
rype
Range
output!
ігапіс-агн
nputl
TO*
(0 1]
Pie Ed* Vim
Рис. 6.1. Основное окно редактора нечётких структур FIS Editor
Нечёткий регулятор представлен структурной схемой состоящей из трёх основных блоков: блок фаззификации (жёлтого цвета), база нечётких продукционных правил (белого цвета) и блока дефаззификации (голубого цвета). Кроме того, основное окно редактора содержит пять выпадающих меню, которые определяют настройки алгоритмов нечётких логических выводов.
Рис.
6.2. Основное меню
FIS
Editor
Рис. 6.3. Пункт
меню Edit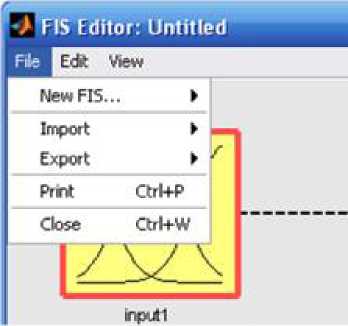
New FIS... - создание новой структуры нечёткого логического регулятора, выбор алгоритма нечёткого логического вывода Мамдани/Сугено;
Import - загрузка данных из файла или рабочей области Matlab;
Export - сохранение данных в файла или рабочую область Matlab;
Print - печать структуры нечёткого логического регулятора;
Close - закрытие окна редактора.
Для набора основных па
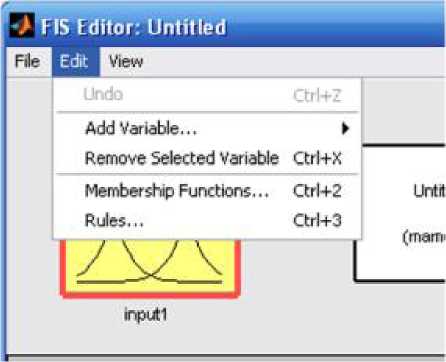
раметров функций принадлежности и для переключения между окнами FIS Editor нечёткого логического регулятора используется пункт меню Edit представленный на рис. 6.3.
Пункт меню Edit содержит следующие команды:
Undo - отмены последней команды или действия;
Add Variable... - добавление лингвистической переменной или входного сигнала нечёткого логического регулятора;
Remove Selected Variable - удаление лингвистической переменной или входного сигнала нечёткого логического регулятора;
Membership Functions... - переключение к окну редактирования параметров функций принадлежности Membership Functions Editor (рис. 6.5);
Рис.
6.4 Пункт меню View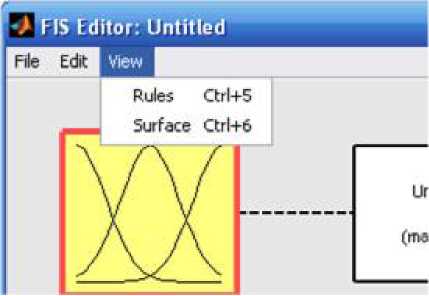
Пункт меню View (рис. 6.4) содержит следующие команды:
Rules - осуществляет переход к окну Rule Viewer, позволяющего проследить в пошаговом режиме направление нечёткого логического;
Surface - выводит поверхность зависимости вход/выход нечёткого логического регулятора.
Необходимо также отметить, что переход между основными окнами FIS Editor (рис. 6.5, 6.6) возможен при помощи двойного щелчка мышью на соответствующем блоке структуры нечёткого логического регулятора.
Me
Ed* v*\4
F
S vamab es
Membership
function plots P™ pentt:
ҐЧМІ
ЙДрігіІ
rifiut variable Tncttl”
Current
Variable Name ІпріЛІ
Тур* ІГ(*1
Rena* Гі|
Rnnga r.i
h
і
Cut rent Membership FgndUcn (cic* on MF to select) "*** mil
T^P* ІГІШІ
Pflrems Г*"/«
n
-ПЛОПД;
п*
в
Las?
Rfativ
Рис.
6.5
Главное
окно Membership
Functions Editor
Рис.
6.6
Редактор
базы
нечётких продукционных правил Rule
Editor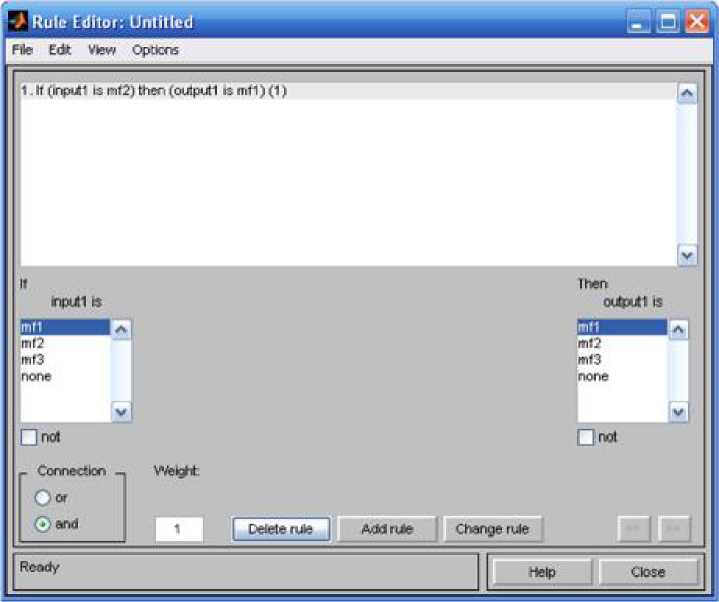
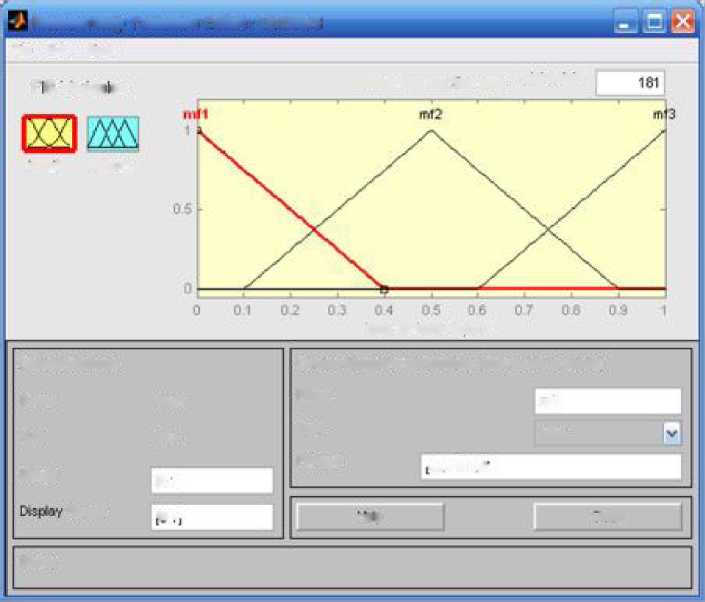
Каждое из основных окон имеет ряд особенностей обусловленных настройкой основных параметров представленных в структуре нечёткого логического регулятора.
Редактор Membership Functions Editor позволяет задавать вид, форму, количество функций принадлежности, а также их параметры. Окно данного редактора содержит следующие команды:
FIS Variables - список лингвистических переменных используемых в текущей структуре нечёткого логического регулятора;
Membership Functions Plots - координатная плоскость на которой иллюстрируются функции принадлежности с параметрами выбранными пользователем;
Range - диапазон регулирования;
Display Range - отображаемый диапазон регулирования;
Name - заданное имя нечёткого терма;
Type - выпадающее меню, позволяющее осуществлять выбор типа функции принадлежности для конкретного терма;
Params - задаёт параметры функции принадлежности нечёткого терма на плоскости стандартным для языка инженерных вычислений Matlab способом.
Окно редактора Rule Editor (рис. 6.6) позволяет синтезировать нечёткую продукционную базу знаний нечёткого логического регулятора. Команды строки основного меню аналогично выше описанным режимам редактора структуры нечёткого управления позволяют переключаться между главными окнами, осуществлять сохранение и загрузку ранее созданной структуры, выводит окна Rule Viewer и Surface Viewer. Особенностью для данного редактора является пункт меню Options позволяющий представить вид нечёткого продукционного правила в удобном для пользователя виде: лингвистическом, символическом, и матричном (рис. 6.7), а также произвести выбор языка вывода.
Рис. 6.7 Пункт меню Options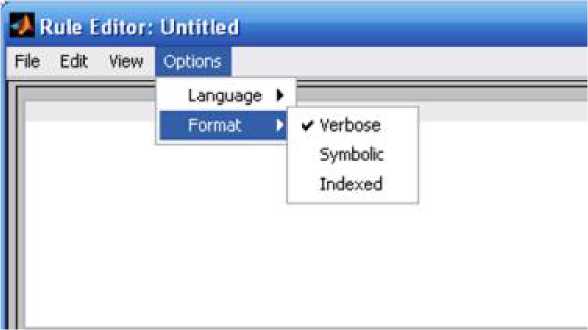
Окно данного редактора представляет собой набор полей в котором отображаются внесённые в структуру нечёткого регулятора при помощи Membership Functions Editor имена нечётких термов и составленные пользователем нечёткие продукционные правила. Кроме того, данный редактор содержит следующий набор команд:
Not - поле для установки отрицания нечёткого терма;
Connection - выбор связки нечётких термов для нечётких регуляторов имеющих два и более входа.
Weight - установка веса выбранного нечёткого продукционного правила.
Delete rule - удаление выбранного правила;
Add rule - добавление составленного правила;
Change rule - изменение выбранного правила;
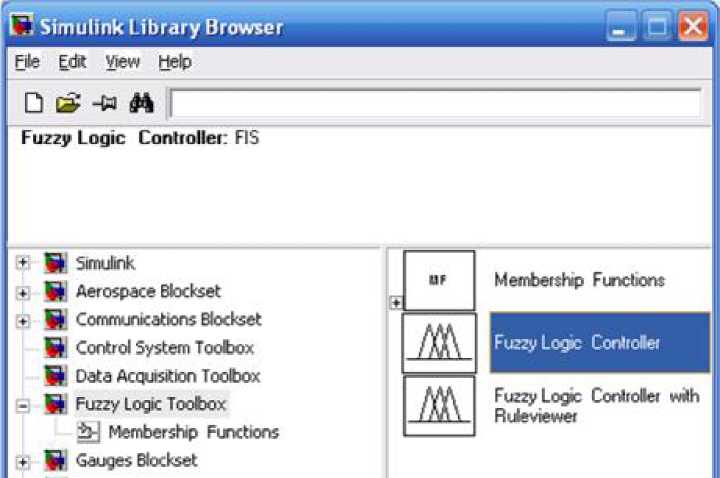
При визуальном моделировании в среде Simulink необходимо добавить звено Fuzzy Logic Controller, который представлен в библиотеке Sim- ulink Library Browser по следующему пути Fuzzy Logic Toolbox^Fuzzy Logic Controller (рис. 6.8).
Затем открыв этот блок двойным нажатием левой кнопки мыши, ввести имя нечёткого регулятора. Важно помнить, что таким же именем должен быть назван и файл, сконструированный в редакторе нечёткого управления Fuzzy Logic Toolbox.
Рис.
6.9 Экспорт данных в рабочую область
Рис.
6.8 Расположение
звена Fuzzy
Logic Controller
в
среде
Simulink
Для
корректной работы нечёткого регулятора
в пакете Simulink,
необходимо предварительно
экспортировать данные в рабочую область:
для этого в окне редактора нечёткого
управления: File^Export^To
workspace, кроме того данная процедура должна повторяться после внесения любых изменений в структуру нечёткого регулятора (рис. 6.9).
Для сохранения данных сконструированного нечёткого регулятора используется функция в главном окне редактора нечёткого управления:
File^Export^To Disk, для загрузки уже готового и настроенного нечёткого регулятора необходимо в редакторе выбрать в меню: File^Import^From disk.
Важно отметить, что при конструировании нового нечёткого логического регулятора связи между основными блоками его структуры - фаз- зификацией, дефаззификацией и базой знаний, отражены в виде пунктирных линий (см. рис. 6.1), что сигнализирует о том, что эти блоки не заполнены или не сконструированы. Только при синтезе всех вышеприведённых блоков и сохранении структуры нечёткого логического регулятора на диск или в рабочую область Matlab, связи принимают полноценный характер и отображаются в окне редактора FIS Editor в виде сплошных линий.
В зависимости от выбранного алгоритма нечёткого логического вывода блок дефаззификации может иметь различный вид. При использовании алгоритма Мамдани, данный блок аналогичен блоку фаззификации. При выборе алгоритма Сугено, в соответствии с его особенностями, он несколько преобразуется (рис. 6.10).
В отличие от окна редактора Membership Functions Editor для алгоритма Мамдани, строка команды Type при использовании алгоритма нечёткого логического вывода Сугено принимает два значения constant и linear, что соответствует алгоритму Сугено нулевого порядка или упрощенному алгоритму нечёткого логического вывода и алгоритму Сугено первого порядка. Такой вид блока дефаззификации обусловлен особенностями самих алгоритмов нечёткого логического вывода.
Кроме того, Fuzzy Logic Toolbox позволяет настраивать нечёткие логические регуляторы с алгоритмом вывода Сугено с использованием адаптивной нейронной сети и редактора Anfis Editor (рис. 6.11). Данный редактор вызывается командой из строки основного меню Edit^Anfis...
Рис.
6.10 Основное
окно редактора нечётких структур
Рис.
6.11 Редактор настройки адаптивной
нейронной
сети Anfis
Editor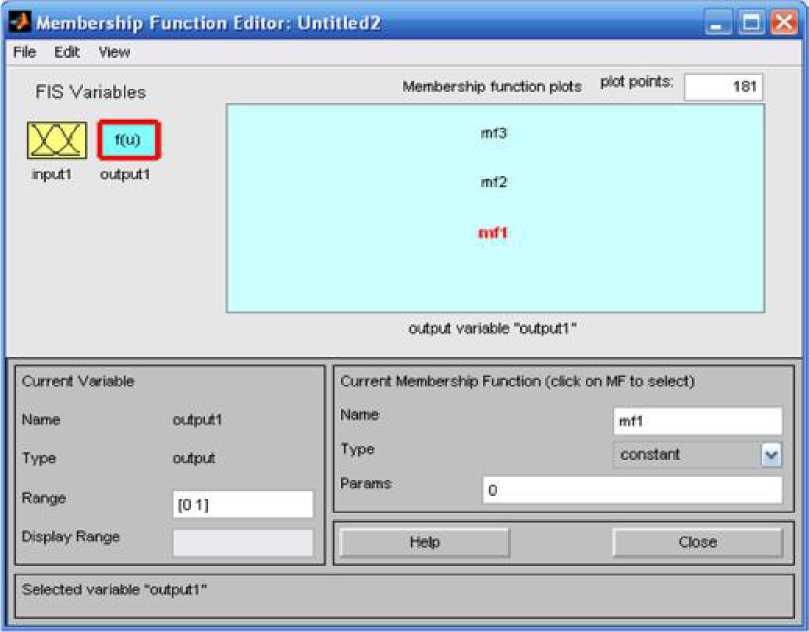
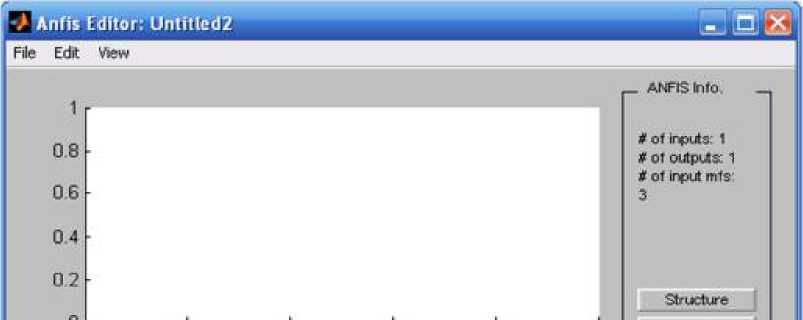
В окне редактора Anfis Editor представлена координатная плоскость позволяющая проследить процесс обучения нечёткого логического регулятора, сравнивая кривую обучения и кривую, например, переходного процесса в системе построенной с применением классических принципов регулирования. Окно данного редактора разделено на несколько блоков, в каждом из которых представлен определённый набор команд.
Блок загрузки данных Load data позволяет осуществить выбор данных для синтеза нечёткого регулятора при помощи адаптивной нейронной сети. Данные для загрузки разделены на несколько типов: обучающие (training), тестовые (testing), проверочные (checking) и демонстрационные (demo). Загрузка все типов данных осуществляется из рабочей области Matlab или файла, в зависимости от установленного маркера From, посредством нажатия кнопки Load Data. Очистка данных производится нажатием кнопки Clear Data.
Блок синтеза нечёткой структуры Generate FIS выводит дополнительное диалоговое окно позволяющее пользователю осуществить выбор количества входных функций принадлежности, их тип из предоставленного языком инженерных вычислений Matlab, а также выбор алгоритма нечёткого логического вывода - упрощённый алгоритм или алгоритм Сугено первого порядка. Функции Load from disk и Load from work sp. позволяют загрузить уже синтезированную нечёткую структуру с диска или рабочей области. При установке маркера в поля команд Grid partition или Sub. clustering осуществляется проектирование новой нечёткой структуры с алгоритмом вывода Сугено.
Блок обучения нечёткой структуры Train FIS позволяет выбрать алгоритм обучения нейронной Optim. Method сети: гибридный hybrid или обратного распространения backpropa, точность обучения Error Tolerance и количество эпох обучения Epochs. Запуск процесса обучения адаптивной нейронной сети осуществляется нажатием кнопки Train Now.
Блок тестирования нечёткой структуры Test FIS позволяет сравнить синтезированный нечёткий регулятор с необходимыми эталонными данными: тестовыми, проверочными или обучающими.
Информационный блок синтезированной нечёткой структуры ANFIS info предоставляет информацию о количестве информационных входов нечёткого логического регулятора, количестве выходов, количестве функций принадлежности и структуре обученной нейронной сети.
Рассмотрим настройку нечёткого логического регулятора с алгоритмом Мамдани на следующем примере.
Рис. 6.12 Модель объекта управления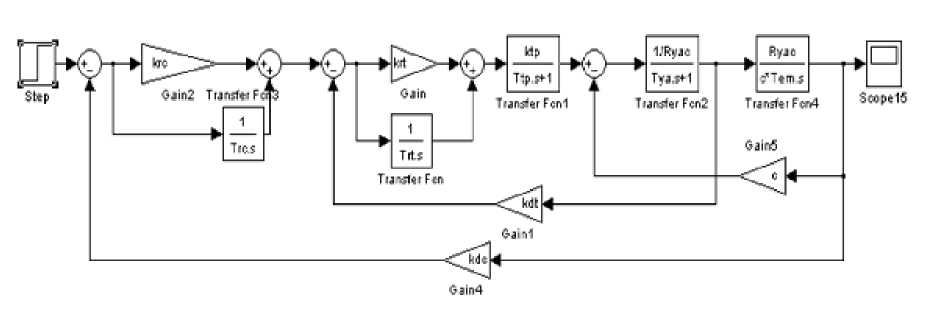
Проиллюстрируем синтез нечёткой системы управления на простейшей модели электропривода третьего порядка, представленной на рис 6.12. Нечёткий регулятор скорости с алгоритмом вывода Мамдани будет содержать две входные лингвистические переменные и одну выходную. Количество нечётких термов внутри каждой лингвистической переменной может быть произвольным.
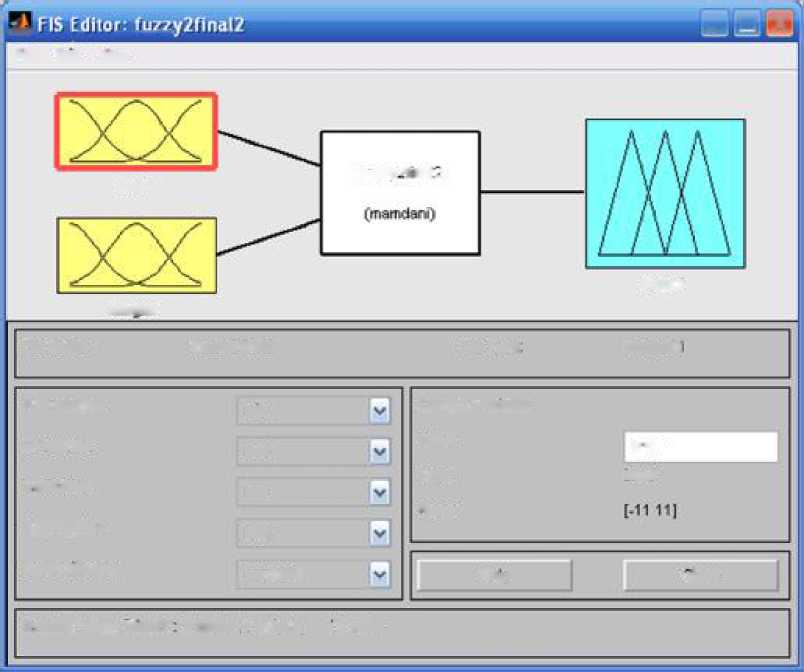
Функциональная схема нечёткого логического регулятора представлена на рис 6.13.
“
."
FIS
Mane:
Error
Integral
rurzy?rmai2
fLrzy’l
vF.1
РІ5
Туре
Oulpif
пїаіиаап
And
methflP Orrnettl«i bn
plication Aggregation
Deluzzjficaion
min
max
min
max
centroid
Current
УвгиИе
НИИ
Type
Range
Hep
Eiror
trrplj
'.lose
System
"(uziy2(nai2" 2inpii£, i oUDUt.ana S rules
Рис. 6.13. Функциональная схема НЛР с алгоритмом вывода Мамдани
Рис.
6.14. Структурная схема нечёткой системы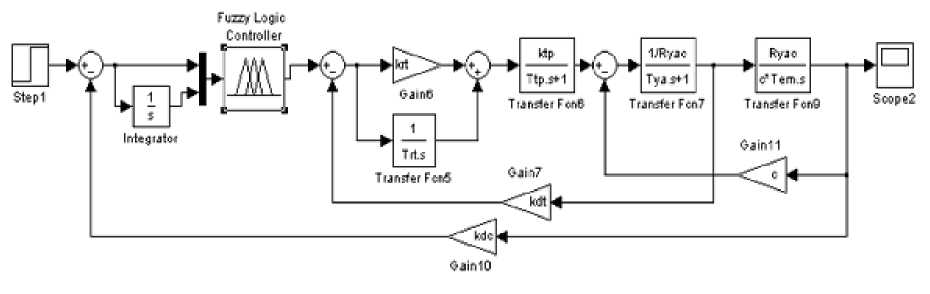
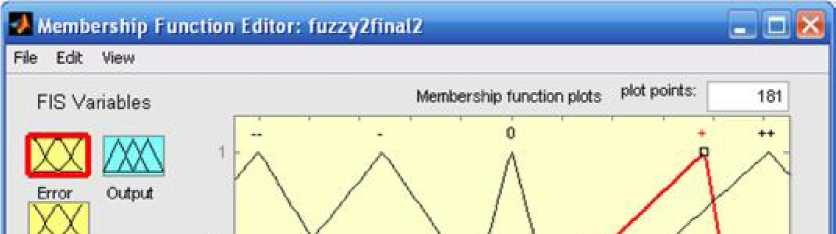
Пусть ведённые лингвистические переменные и нечёткие термы имеют следующий вид, представленный на рис. 6.15.
-10
-в -в -4
-2 0 2 4
ВО 10 input
varietal
"Error"
Current
VateMe Man«
Error
Type aipta
Range
(Till)
Current
Membership Function (cfck on MF to select)
Wan*
+
JW*
trmf |
v
PsfWlS
югб&е.ээ^
Display
Range [-111Ц
Help
Close
Рис. 6.15. Окно редактирования нечётких термов лингвистической переменной «Error» (лингвистическая переменная «Error» - ошибка системы управления состоит из 5 нечётких термов: (--) - большая отрицательная ошибка системы управления, (-) - средняя отрицательная ошибка системы управления, (0) - нулевая ошибка системы управления, (+) - средняя положительная ошибка системы управления, (++) - большая положительная ошибка системы
управления)
Лингвистические переменные и нечёткие термы для интеграла ошибки могут быть представлены в виде, показанном на рис. 6.16. Аналогичным образом формируются лингвистические переменные и нечёткие термы для выходной переменной, которые приведены на рисунке 6.17.
File
Edit
View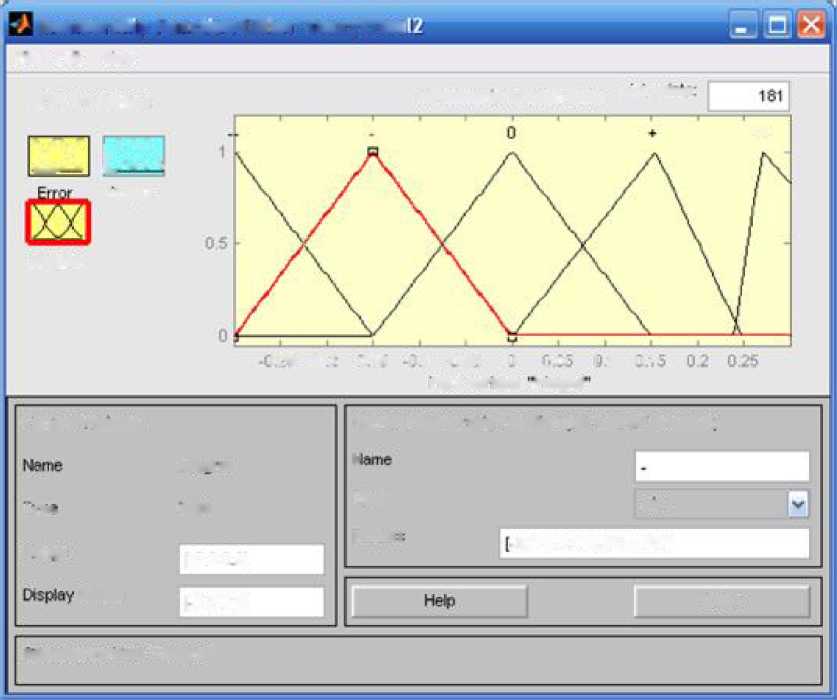
FIS
Variables
XX
/m
output
c*
mt
eqrm
r,25 -0,2 41,15 -0.1 -0.05 0 J 05 0 1 0.1!
Current
variable
.
mteceal
Current
Membership Flection rcRek ОГ»
MF
to $ОШ'1
h
•
v'F-
nput
Type
Irirnf
mm \
Kanr^e
1-0-3 0 3]
Range |-0.3 0.3]
selected variable "integfar
-0.3 -0.15 -5.551 e-01 7]
Close
input variable Integral
Рис. 6.16. Распределение функций принадлежности лингвистической переменной «Integral» (лингвистическая переменная «Integral» - интегральная составляющая ошибки системы управления, состоит из 5 нечётких термов: (--) - большое отрицательное отклонение интегральной составляющей ошибки системы управления, (-) - среднее отрицательное отклонение интегральной составляющей ошибки системы управления, (0) - нулевое отклонение интегральной составляющей ошибки системы управления, (+) - среднее положительное отклонение интегральной составляющей ошибки системы управления, (++) - большое положительное отклонение интегральной составляющей ошибки
системы управления)
FIS
Variables
Membership
Unction plots P“ P«f*s
181
Crrqr Output
Integral
■
ISO -100
euttiti variable "OutpU
Cerent Variable Name Output Type output Ran®e 11-150150} |
CurCfit Membet£h4> Function (CbClf on KF lo «elect) Neme ТУР® 1шЫ g |
PafSmS 1-190-30.56 0) |
|
|
|
Display Range M50 1 50J |
Help П:::- |
|
|
Selected variable “Output“ |
|
Рис. 6.17. Распределение функций принадлежности лингвистической переменной «Output» (лингвистическая переменная «Output» - сигнал управления (выходной сигнал нечёткого регулятора) состоит из 5 нечётких термов: (--) - большое отрицательное отклонение сигнала управления, (-) - среднее отрицательное отклонение сигнала управления, (0) - нулевое отклонение сигнала управления, (+) - среднее положительное отклонение сигнала управления, (++) - большое положительное отклонение сигнала управления)
База нечётких продукционных правил необязательно должна содержать максимально возможное количество правил (для данного регулятора 25), достаточно чтобы она удовлетворяла требованиям полноты и непротиворечивости. Для нашего примера база правил будет состоять из пяти продукционных правил (рис. 6.18) следующего вида:
Правило 1. ЕСЛИ Error есть (++) ТО Output есть (++);
Правило 2. ЕСЛИ Error есть (0) И Integral есть (0) ТО Output есть (0); Правило 3. ЕСЛИ Integral есть (++) ТО Output есть (0)
Правило 4. ЕСЛИ Error есть (+) ТО Output есть (+)
Правило 5. ЕСЛИ Error есть (-) И Integral есть (+) ТО Output есть (-)
Рис. 6.18. База нечётких продукционных
правил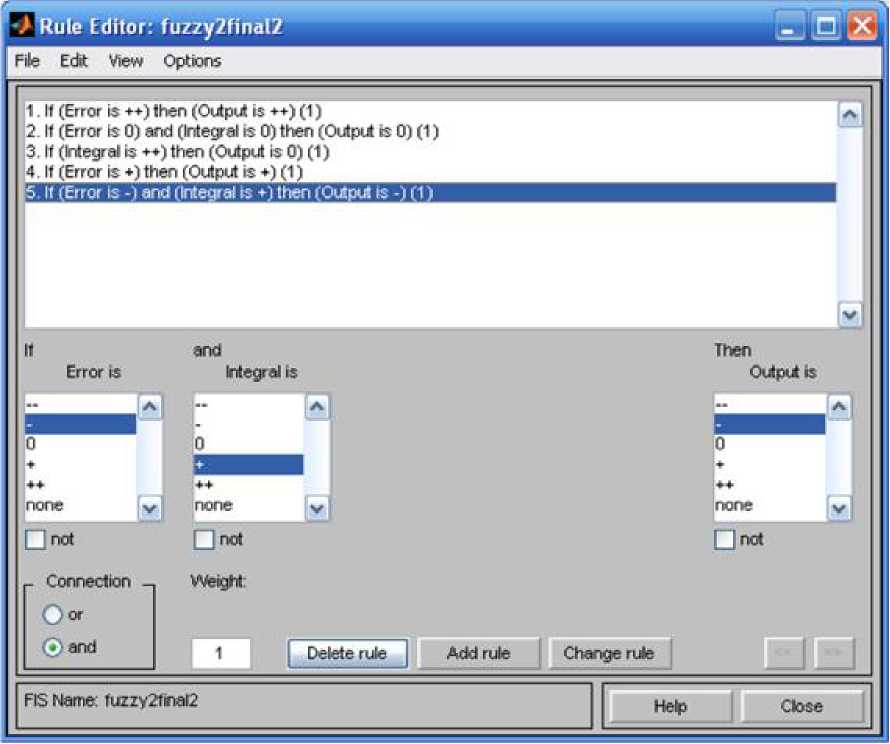
Проверку настройки алгоритма вывода достаточно удобно проверять при помощи редакторов Rule Viewer и Surface Viewer (рис. 6.19, 6.20).
File
Edit View Options
Error
“ 0
Integral
= Ü
Output
- 1,71 e-MS
150
i-.n
input
[0
Gl
PlOt
pOlrtt. irtn
Move;
it-ц
riant
down up
Opened
system tuzzy2finel2.
5
rules
Help
Close
Рис. 6.19. Экранная форма Rule Viewer
Окно Rule Viewer позволяет разработчику нечёткой системы управления полностью контролировать процесс нечёткого вывода на любом его этапе. На рис. 6.19 представлен вывод при значениях входных лингвистических переменных «Error»=0 и «Integral»=0. При таких значения переменных в выводе участвует второе продукционное правило из базы знаний. Далее с использованием операции максимума формируется итоговое агрегированное нечёткое множество, на основе которого, с применением цент- роидного метода приведения к чёткости вычисляется «чёткое» значение выходной переменной. Кроме того, пользователь имеет возможность проследить направление нечёткого вывода для любых значений входных лингвистических переменных, путём ввода их значении в строке Input.
Error
Fife Edit View Optcms
1UJ
-и
0
X
(input!
Error
V
(riwtl
Hegral v
’
(OUpliJ
Output
X
grids
V
^Kts:
КеТ.
1Г|(ХЛ
Help
'.:ose
Ready
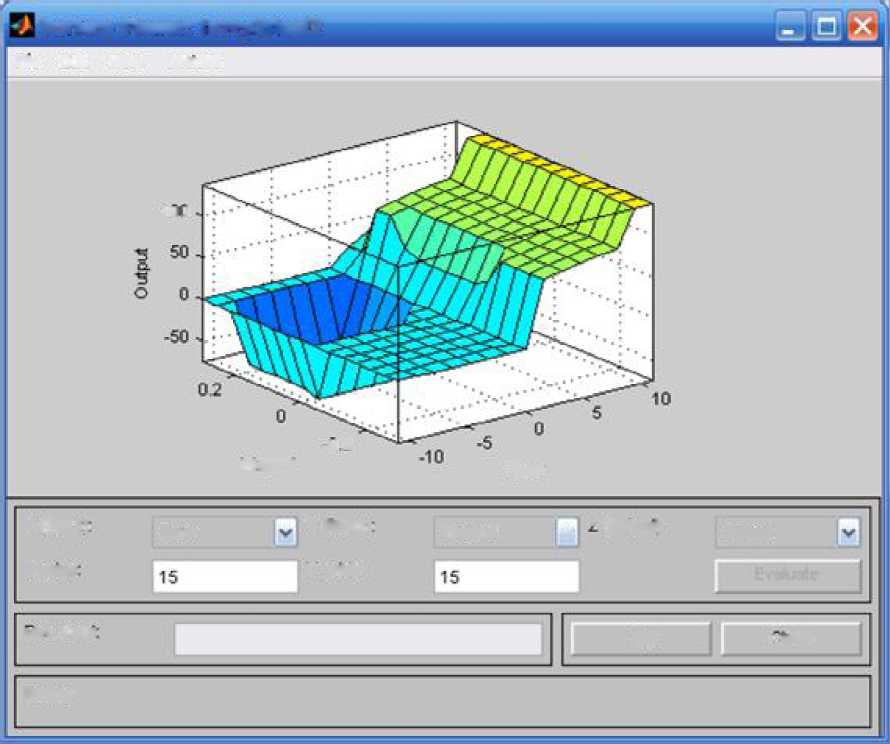
Рис. 6.20. Поверхность нечёткого вывода
Приведённая на рис. 6.20 поверхность нечёткого вывода представляет собой зависимость между значениями основных лингвистических переменных и позволяет сделать выводы об адекватности настройки нечёткой системы управления.
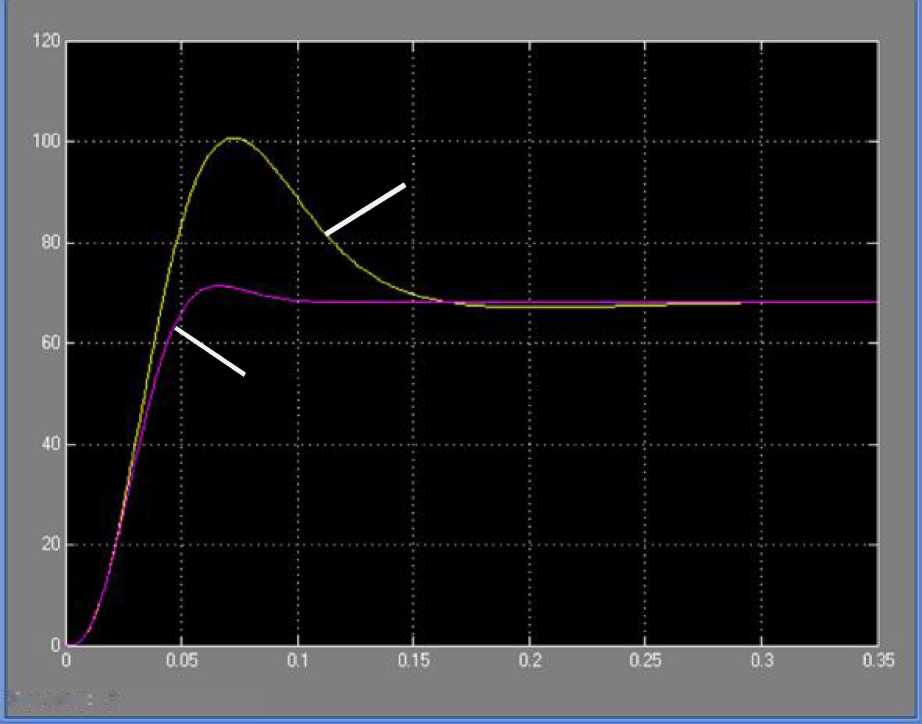
Результаты
моделирования представлены на рис.
6.21. По представленным динамическим
характеристикам можно сделать вывод о
том, что нечёткая система управления
даёт существенно лучшие показатели
регулирования по сравнению с
классической системой: перерегулирование
уменьшается на 30% и время переходного
процесса сокращается более чем в 2 раза.
Г7 5
ІкогоїТ
ш
э
X
р_|
Ш РРР
А И И
в д ч
'
1
2
Тітес^сеІ О
Рис. 6.21. Динамические характеристики систем управления (1 - с классическим регулятором; 2 - с нечётким логическим регулятором)
На примере классической системы регулирования, представленной на рис. 6.22, рассмотрим особенности настройки нечёткой системы управления с алгоритмом Сугено. Проиллюстрируем синтез нечёткой системы управления на аналогичной простейшей модели электропривода третьего порядка (рис. 6.22). Нечёткий регулятор скорости с алгоритмом вывода Сугено будет содержать две входные лингвистические переменные и одну выходную. Количество нечётких термов внутри каждой лингвистической переменной может быть произвольным.
электроприводом
постоянного тока
Функциональная схема нечёткого логического регулятора представлена на рисунке 6.23.
. п X
Рис.
6.22. Структурная схема классической
системы управления
Егґсг
Р^оТоїад^г»
(гипегіо)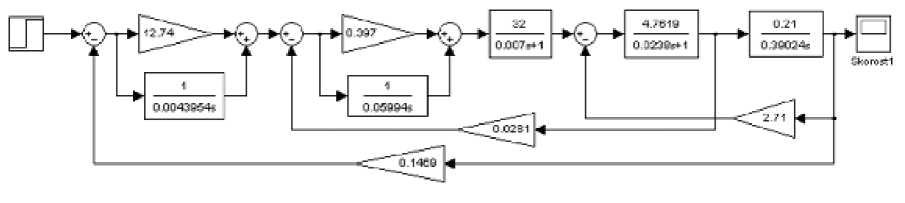
ОЧр*
□алуяіллв
ИЗМаше Яс9То(!*5*і9Єпв Р£Туі» «идоо
Апа
те№<хі ”
Огчйіиоа
р,оьо< ^
адп*
Еігй
ІПКЇІСЙІт
Адуедаїіоп
Туре
іГцЛчі
КйПд*
(-50110)
0є{И£2ІИЇСв(ЮП!
\ft1flVPf
1
\?\
Неір
Оозе
Єу-ЕІєт ТгедТокаОидвпо'’ 2
іприн , 1 оніри!,
егчі 51 іім
Рис. 6.23. Функциональная схема нечёткого логического регулятора с
алгоритмом вывода Сугено
Структурная схема нечёткой системы управления после замены классического регулятора тока на нечёткий примет следующий вид (рис. 6.24)
Рис. 6.24. Система управления с нечётким
логическим регулятором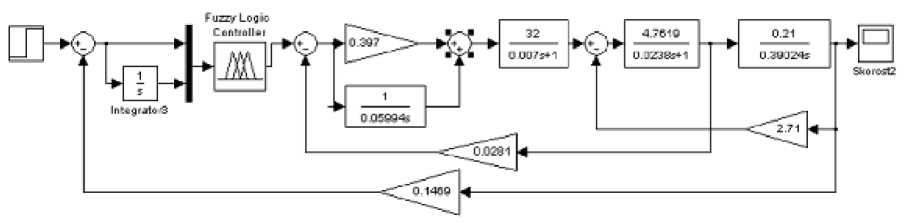
Введённые нами лингвистические переменные и нечёткие термы имеют вид, представленный на рисунках 6.25-6.27. Такой выбор распределения функций принадлежности в заданном диапазоне регулирования обусловлен экспертными знаниями об особенностях функционирования объекта управления.
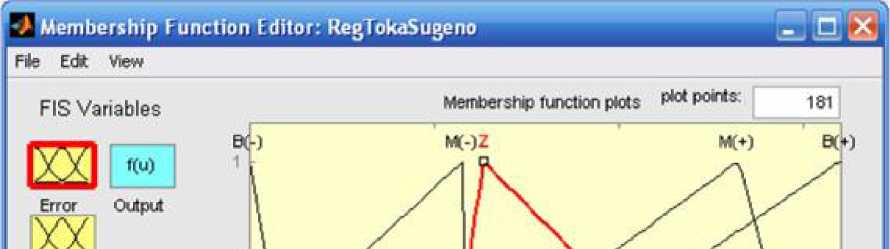
Current
Variate Nftrfte Error Туре
npUt
Cirrem
Memberih4) Function (ok* on rf lo serect)
Nome
2
Ifflll
V
1-50 mi
рдайл1г
I6.0S13.3
66.611
Display
Range
Help
Close
Рис. 6.25. Окно редактирования нечётких термов лингвистической переменной «Error» (лингвистическая переменная «Error» - ошибка системы управления состоит из 5 нечётких термов: B(--) - большая отрицательная ошибка системы управления, M(0) - средняя отрицательная ошибка системы управления, Z - нулевая ошибка системы управления, M(+) - средняя положительная ошибка системы управления, B(+) - большая положительная ошибка системы
управления)
Рис. 6.26. Окно редактирования нечётких
термов лингвистической переменной
«Derivative» (лингвистическая
переменная «Derivative» -
дифференциальная составляющая ошибки
системы управления состоит из 5 нечётких
термов: B(-) - большое
отрицательное отклонение дифференциальной
составляющей ошибки системы управления,
M(-) - среднее отрицательное
отклонение дифференциальной составляющей
ошибки системы управления, S(-)
- малое отрицательное отклонение
дифференциальной составляющей ошибки
системы управления, Z -
нулевое отклонение дифференциальной
составляющей ошибки системы управления,
M(+) - среднее положительное
отклонение дифференциальной составляющей
ошибки системы управления)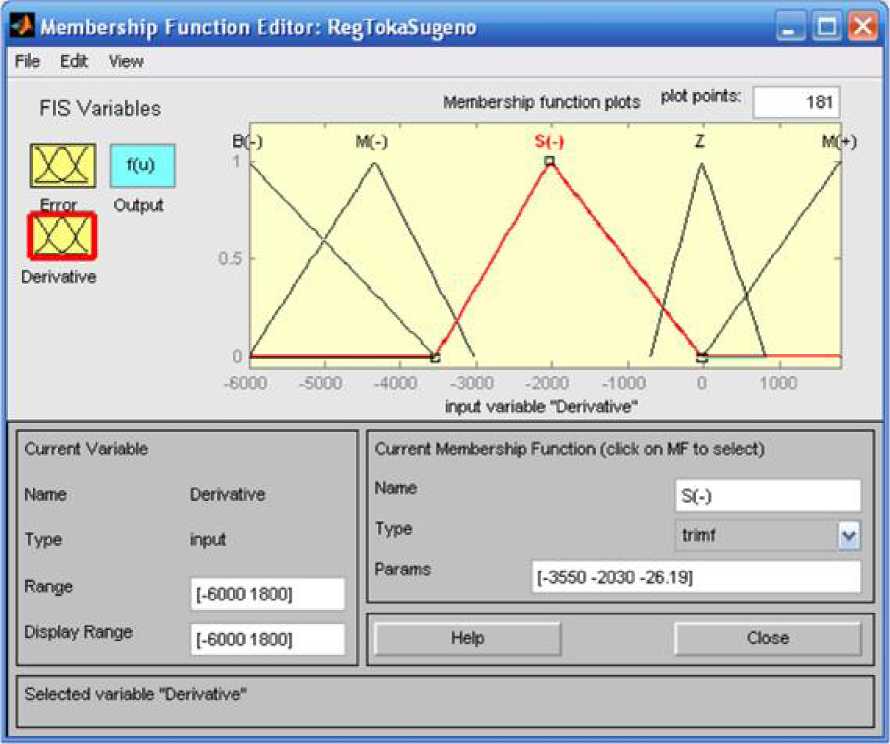
Рис. 6.27. Окно редактирования нечётких
термов лингвистической переменной
«Output» (лингвистическая
переменная Output - сигнал
управления (выходной сигнал нечёткого
регулятора), при использовании упрощённого
алгоритма нечёткого логического вывода
будет состоять из следующего набора
констант [-80; 8; 55; 180; 230])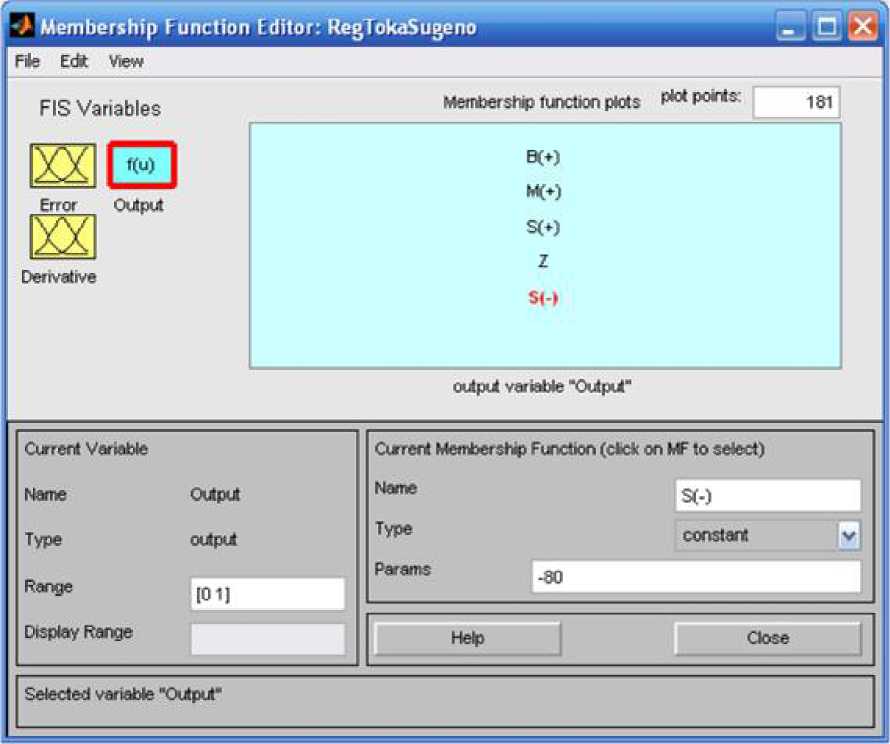
База нечётких продукционных правил для нашего примера будет иметь вид (рис. 6.28):
Правило 1. ЕСЛИ Error есть B(+) ТО Output=230;
Правило 2. ЕСЛИ Error есть Z И Derivative есть Z ТО Output=8; Правило 3. ЕСЛИ Error есть М(-) ТО Output=-80 Правило 4. ЕСЛИ Error есть B(+) ТО Output=55 Правило 5. ЕСЛИ Error есть S(-) ТО Output=-80
Fife
If
(Error is Bf +)) then (Output ns
H+))
(1)
It
(Error is Z) and (Derivative is Z)then (Output rs Z)(1)
It
(Error is MO)) then (Output e
S(-)) (1)
If
(Error is Bi+))then (Output к
Mi
*)) Ці
it
(Derivative is S(-)l then (COpU
is
SOjj (і
1
ЙП.1
-Г-Г--П
Error
is
Derivative
is
Output«
M(*)
B(*J
none
MC*)
none
Jnoi
□ not
□ net
Connection
О or
and
Weight
Detete
rule
FIS
Name RegTokaiSusenKj
Help
Close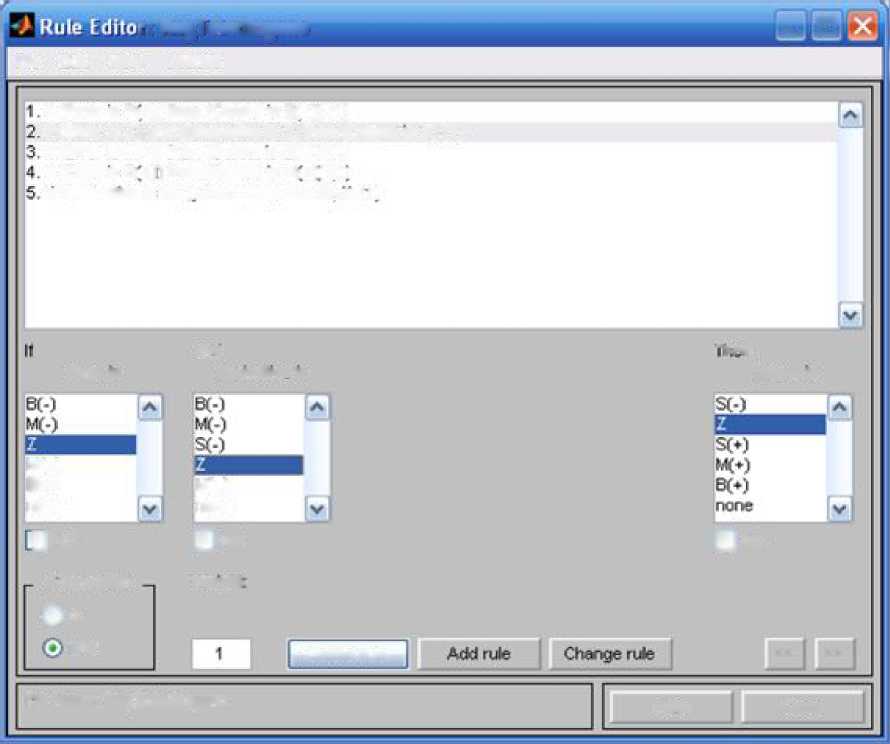
Рис. 6.28. База нечётких продукционных правил
Проверка настройки алгоритма вывода, а также её качество и адекватность достаточно удобно проверять при помощи редакторов Rule Viewer и Surface Viewer (рис 6.29, 6.30).
Рис. 6.29. Результаты проведения нечёткого
вывода Сугено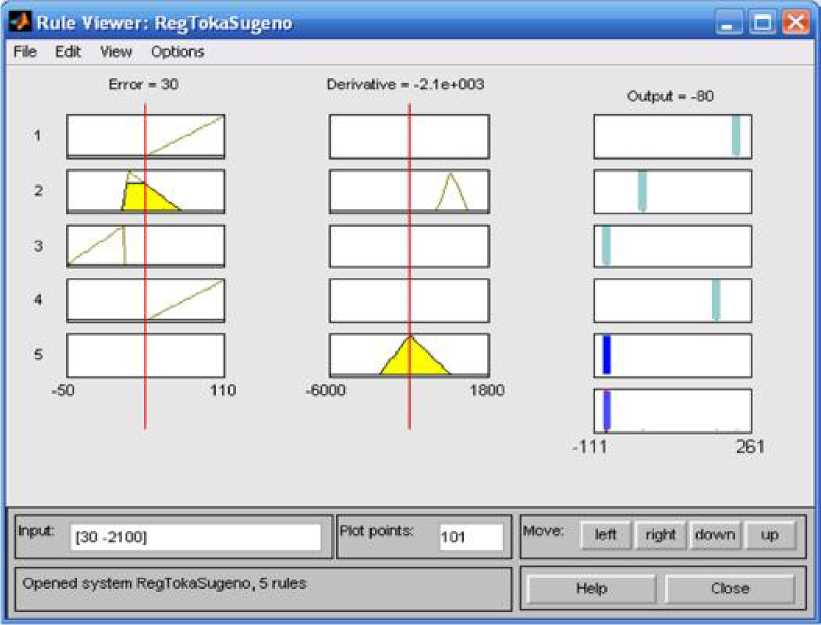
Рис. 6.30. Поверхность нечёткого вывода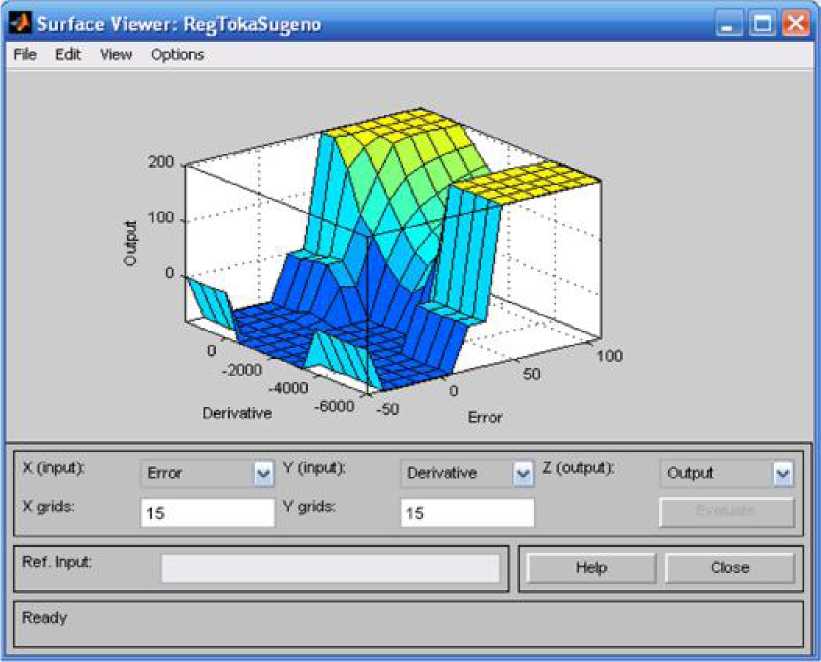
Динамические характеристики классической системы регулирования и нечёткой системы управления с алгоритмом вывода Сугено представлены на рис. 6.31.
Рис. 6.31. Динамические характеристики
систем управления (1 - с классическим
регулятором; 2 - с нечётким логическим
регулятором)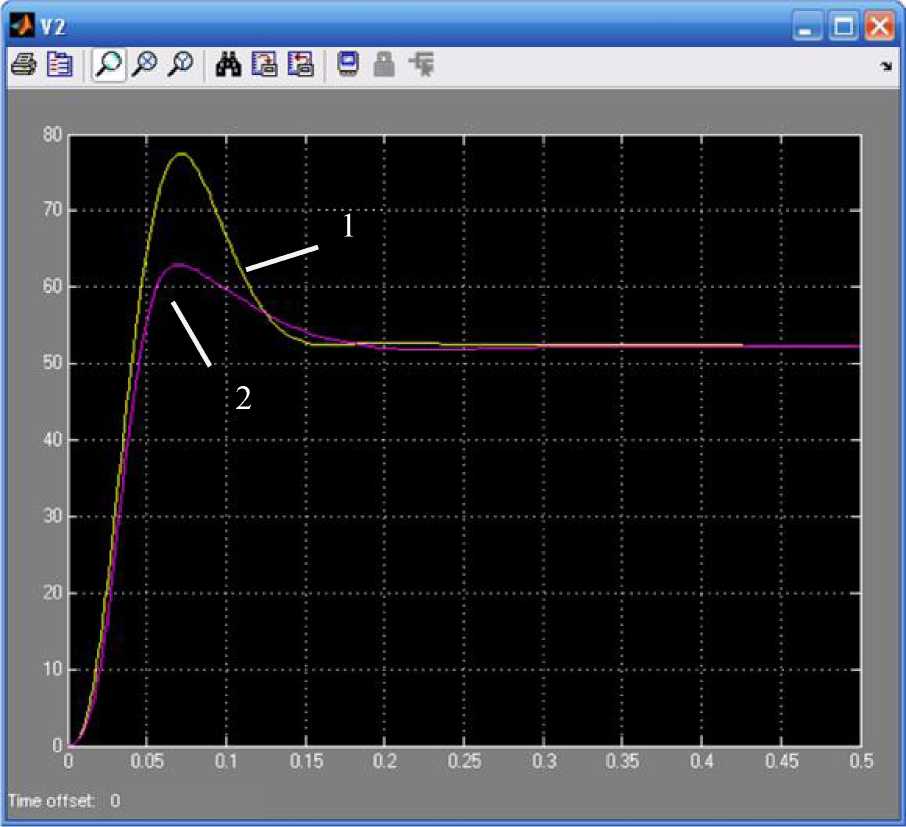
Реализация законов управления с применением нечёткого логического регулятора с алгоритмом вывода Сугено позволила снизить перерегулирование в системе в 2 раза, по сравнению с классической системой управления, сохранив при этом её быстродействие.
ЗАКЛЮЧЕНИЕ
Данное пособие не претендует на исчерпывающее изложение теоретических и практических аспектов построения нечётких систем управления. Представленный материал даёт возможность специалисту познакомиться и освоить базовые приёмы синтеза нечётких регуляторов и анализа интеллектуальных систем управления, научиться основным приёмам моделирования нечётких систем регулирования с применением языка инженерных вычислений Ма1ЬаЬ. Наличие большого числа примеров даёт возможность пользователю проверить приобретённые навыки по имитационному моделированию нечётких систем.
Авторы надеются, что изложенный в данном учебном пособии материал повысит интерес студентов, преподавателей и специалистов к проблемам проектирования нечётких систем управления.
Авторы с благодарностью примут рекомендации и замечания по содержанию данного учебного пособия, которые можно переслать на электронный ящик: kepapu@knastu.ru.
БИБЛИОГРАФИЧЕСКИМ СПИСОК
Braee M., Rutherford D.A. Theoretical and Linguistic Aspect of the Fuzzy Logic Controller // Automation, Perg. Press. - 1979. - Vol.12. - P. 553 - 557.
Carter L.A., Hagne М.Т Fuzzy Control of Raw Mix Permeability of Sinter Plant. Proc. Fuzzy Workshop, QMC, London. 1976.
Fuzzy Logic Toolbox User’s Guide //The MathWorks, Inc., 1998.
Nguyen D. Neural Networks for Self-Learning Control Systems // IEEE Control Systems. — 1990. — Vol. 10. - P. 18 - 23.
Кончин А.В., Соловьев В. А. Алгоритм синтеза нечёткого логического регулятора по прямым показателям качества // Информатика и системы управления, 2003, № 2 - С. 94 - 100.
Procyk T.J., Mamdani E. H. A Linguistic Self-Organizing Process Controller // Automatica. - 1979. - Vol.15. - P. 15 - 30.
Scharf H., Mandic N., Mamdani E.H. A self-organizing algorithm for the control of a robot arm // Int. J. Robotics and Automation. - 1986. - Vol.1, №1. - P. 33 - 41.
Zadeh L. The role of fuzzy logic in the management of uncertainty in expert systems // Fuzzy Sets a. Systems. - 1983. - Vol. 11, N 3. - P. 199 - 227.
Zadeh L. A. Fuzzy logic = computing with words. - IEEE Trans. on Fuzzy Systems, v. 4, 2, 1996. - P. 103 - 111.
А.с. 1224503 СССР, МКИ F22 G 5/00. Автоматическая система регулирования температуры пара котлоагрегата / А. А. Москаленко, В. А. Коробский, Г.Т. Кулаков, А.Т. Кулаков (СССР). - № 3693127/24; Заявлено 13.01.81; Опубл. 13.04.86., Бюл. № 14. - 1с.
Батыршин И.З. Иерархическая кластеризация на основе нечисловой информации о близости//Нечисловая статистика, экспертные оценки
и смежные вопросы/Тез. докл. II Всесоюзн.конф. по статистич.и дис- кретн. анализу нечисловой информации и экспертным оценкам. -
М.: Таллин, 1984. - С. 277.
Блишун А.Ф., Знатнов С.Ю. Обоснование операций теории нечётких множеств. - В кн.: Нетрадиционные модели и системы с нечёткими знаниями.
Брайсон А., Хо Ю-ши. Прикладная теория автоматического управления. М.: Мир, 1972. - 366 с.
Васильев В.И. Ильясов С.В. Интеллектуальные системы управления с использованием нечёткой логики. Учебное пособие. Уфа: Изд.-во УГАТУ, 1995. - 80 с.
Владыко А.Г., Кабалдин Ю.Г., Соловьев В.А. Черный С.П. К вопросу синтеза нечётких регуляторов систем электропривода подач // Нелинейная динамика, фракталы и нейронные сети в управлении технологическими системами: Сб. статей под ред. докт. техн. наук, проф. Кабалдина Ю.Г. - Владивосток: Дальнаука, 2001. - С. 179-183.
Данилов А. Компьютерный практикум по курсу «Теория управления». БтиИпк-моделирование в среде МаБаЬ. МГУИЭ, 2002.
Дорф Р., Бишоп Р. Современные системы управления: Перевод с английского. Лаборатория базовых знаний, 2002.
Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике. - М: Радио и связь, 1990. - 288 с.
Ивашко В.Г., Кузнецов С.О. Оценки правдоподобия в продукционных экспертных системах//Экспертные системы: состояние и перспективы. - М.: Наука, 1989, с. 92-103.
Искусственный интеллект. - В 3-х кн. Кн.1. Системы общения и экспертные системы: справочник/Под ред. Э.В. Попова. - М.:Радио и связь, 1990. - 464 с.
Кандрашина Е.Ю., Литвинцева Л.В., Поспелов Д.А. Представление знаний о времени и пространстве в интеллектуальных системах/Под редакцией Д.А. Поспелова. - Москва, Наука. - 1989. - 328 с.
Кудинов Ю.И. Нечёткие системы управления //Техническая кибернетика. - 1990. - № 5. - С .196-201.
Кутателадзе С.С. Основы теории теплообмена. - 5-е изд., пере- раб. и доп. - М.: Атомиздат, 1979. - 240 с.
Ларичев О.И., Мечитов А.И., Мошкович Е.М., Фуремс Е. М. Выявление экспертных знаний. - М.:Наука, 1989. - 128 с.
Литвак Б.Г. Экспертная информация. Методы получения и анализа.-М.: Радио и связь, 1982. - 184 с.
Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечёткой логикой. - М.: Наука, 1990. - 272с.
Методика расчета динамических характеристик пароперегре- вательных участков котельных агрегатов. Руководящие указания. Вып. 15. ЦКТИ, 1967. - 36 с.
Миркин Б.Г. Проблема группового выбора. - М.: Наука, 1974. - 256 с.
Наладка систем автоматического регулирования барабанных паровых котлов / А.С.Клюев и др. - М.: Энергоатомиздат, 1985. - 280с.
Нечёткие множества в моделях управления и искусственного интеллекта /Под ред. Д.А. Поспелова. М., 1986.
Нечёткие множества и теория возможностей. Последние достижения / Под ред. Р.Ягера М.: Радио и связь, 1986.
Нечёткое управление системами автоматизированного электропривода. / Соловьев В.А., Владыко А.Г., Суздорф В.И., Черный С.П. // Электромеханические преобразователи энергии: Материалы докл. между- нар. научно-техн. конф. - Томск. - 2001. - С. 79 -80.
Орловский С.А. Проблемы принятия решений при нечёткой информации. - М.:Наука, 1981. - 206 с.
Пат. 2044216 РФ, МКИ F22 G 5/12. Автоматический регулятор температуры перегретого пара в многотопливном парогенераторе / И.В.Куртис (Россия). - № 5016653/06; Заявлено 11.12.91; Опубл. 20.09.95. Бюл. № 26. - 2с.
Пат. 5-24401 Япония, МКИ F22 G 5/00. Регулятор расхода питательной воды в барабанном котле / Токке Кохо; Опубл. 07.04.93., № 5611.
Пат. № 2044214 РФ, МКИ F22 В 35/00. Регулятор давления перегретого пара в многотопливном парогенераторе / И.В.Куртис (Россия). - № 5015251/06; Заявлено 02.12.91; Опубл. 20.09.95. Бюл. № 26. - 3с.
Пат. № 2044215 РФ, МКИ F22 G 5/00. Устройство для регулирования температуры пара котлоагрегата / И.В.Куртис (Россия). - № 5015247/06; Заявлено 02.12.91; Опубл. 20.09.95. Бюл. № 26. - 1 с.
Пат. № 2151342 РФ, МКИ F 22 G 5/00. Устройство для регулирования температуры пара котлоагрегата / Соловьев В.А., Владыко А.Г., Легенкин В.С. (Россия). - № 99102392/06; Заявлено 04.02.99; Опубл.
Бюл. № 15. - 3с.
Первозванский А.А. Математические модели в управлении производством. М.: Наука,1975.
Петров В.В., Кочубиевский И.Д., Уланов Г.М. Информационные аспекты автоматического управления технологическими процессами //Изв. АН СССР. Техн. кибернетика. 1967. № 4. С. 3 - 13.
Пивкин В.Я., Бакулин Е.П., Кореньков Д.И. Нечёткие множества в системах управления // http://idisys.iae.nsk.su:8102/fuzzy book.
Пискунов А.И. Процедуры принятия решений в структурированных нечётких системах //АиТ. - 1988. - № 5 - С. 106 - 112.
Пискунов А.И. Эквивалентные преобразования структуры нечётко формализованных систем //АиТ. - 1988. - № 4. - С. 128-137.
Плетнев Г.П. Автоматизированное управление объектами тепловых электростанций.-М.: Энергоатомиздат, 1981 .-268с.
Плетнев Г.П. Автоматическое регулирование и защита теплоэнергетических установок электрических станций. М.: Энергия, 1976. - 286 с.
Поляк Б., Щербаков П. Робастная устойчивость и управление. Наука. 2002.
Поспелов Д.А. Логико-лингвистические модели в системах управления. - М.: Энергия, 1981. - 231с.
Поспелов Д.А. Ситуационное управление: теория и практика.
М.: Наука, 1986. - 288с.
Прикладные нечёткие системы/ К. Асаи, Д. Ватада, С. Иваи и др.; под ред. Т. Тэрано, К. Асаи, М. Сугэно. Перевод с япон. - М.: Мир, 1993. - 368с.
Приходько И.А. Нечёткие структуры систем регулирования возбуждения синхронного генератора // Электричество. - 2002. - № 6. - С. 46-50.
Сазыкин В.Г. Расширение и классификация используемых в задачах электроснабжения нечётких чисел // Электричество. - 1996. - № 6.
С. 33-38.
Семененко М. Введение в математическое моделирование. Со- лон-Р. 2002.
Соловьев В.А. Кончин А.В. Алгоритм и программная реализация синтеза НЛР по прямым показателям качества //Сб. научн. трудов междунар. науч.-т. конф. - ЭЭЭ-2003. - Комсомольск-на-Амуре. - 2003. - 55 - 59.
Соловьев В.А. Кончин А.В. Программа синтеза параметров НЛР по прямым показателям качества. - Свидетельство об официальной регистрации программы для ЭВМ № 2004610573. - 46 с.
Соловьев В.А., Владыко А.Г. Применение мягких вычислений к построению моделей нелинейных систем // Нелинейные науки на рубеже тысячелетий: Материалы междунар. научной конф. - С.Петербург, 1999. с.67.
Соловьев В.А., Владыко А.Г., Легенкин В.С. Применение нечёткой логики в устройствах регулирования энергетическими объектами // Электроэнергетика и энергосберегающие технологии: Межвуз. сб. науч. тр. - Владивосток: Изд-во ДВГТУ, 1998. - с. 125-133.
Соловьев В.А., Гудим А.С., Черный С.П. Программа оптимизации распределения функций принадлежности нечёткого регулятора при заданных показателях качества системы управления. // Свидетельство об официальной регистрации программы для ЭВМ № 2003612124.
Соловьев В.А., Косицын В.Г., Черный С.П., Иванкова Е.П. Оптимизация распределения функций принадлежности при синтезе нечёткого регулятора для систем управления тепловыми процессами. // Информатика и системы управления, 2003, №1. - 73-82.
Справочник по теории автоматического управления / Под ред. Красовского А. А. М.: Наука, 1987. 346 с.
Теория выбора и принятия решений. / Под ред. И.М. Макарова. - М.: Наука, 1982. - 327 с.
Уотермен Д. Руководство по экспертным системам.- М: Мир, 1989. - 388 с.
Х. Гурецкий Анализ и синтез систем управления с запаздыванием. М.: Машиностроение, 1974, 328 с.
Попов Е.П. Прикладная теория процессов управления в нелинейных системах. М: Наука. 1973, 584 с.
Пат. №2323463 Государственный реестр изобретений РФ. Способ компенсации статических нелинейностей./ В.Ф. Горячев, А.С. Гудим, И.В. Зайченко, В.А. Соловьев. Опубликовано: 27.04.2008 Бюл. №12.
Гудим, А.С. Нечеткие алгоритмы компенсации нелинейностей САУ / В. А. Соловьев, И.В. Зайченко - АмГУ: Информатика и системы управления.
Приложение 1
Блок-схема алгоритма, текст программы и инструкция пользователя к методу оптимизации распределения функций принадлежности НЛР
Средой разработки является язык технических вычислений MatLab. Данный выбор обусловлен наличием соответствующего встроенного инструментария.
Программирование блоков фаззификации и дефаззификации нечёткого логического регулятора (FLC) осуществлялось по следующему алгоритму:
задание аналитически желаемого вида переходной характеристики сигнала управления;
перевод численных значений сигнала управления в относительные величины (рис.1);
реализация функции обратного отображения в горизонтальной плоскости и трансформация полученных результатов в новых координатных осях (рис.2).
Итогом полученных преобразований является функция отображения, относительно которой проецируются равномерно распределённые функции принадлежности, и при этом, их вид и количество может варьироваться (рис.3).
Пользователь из ранее смоделированной схемы должен получить сигнал управления, воспользовавшись встроенным блоком Simulink «To Workspace», при этом установив его формат в виде области (array).
Запуск программы осуществляется из командной строки MatLab «flc(tout, simout)».
Порядок работы алгоритма.
После запуска программы производиться объявление глобальных переменных, необходимых для работы подпрограммы. Условный оператор производит проверку на достаточность указанных в командной строке параметров для функции «flc». В случае если переменной action, осуществляющей ветвления предложенного алгоритма, присвоено значение ‘а’, то, производиться обнуление переменных для пересчёта обновлённых данных.
Далее программа формирует массив точек полученного сигнала (рис.1), определяет 5% зону сигнала управления и производит их построение.
После этого следует блок получения и построения уравнения касательной, которая необходима для реализации предложенного метода, по средствам нескольких циклов, условий и ограничений.
Следующим этапом программа производит формирование и построение отображённого модифицированного сигнала (рис.2) и координатной системы с функцией отображения (рис.3).
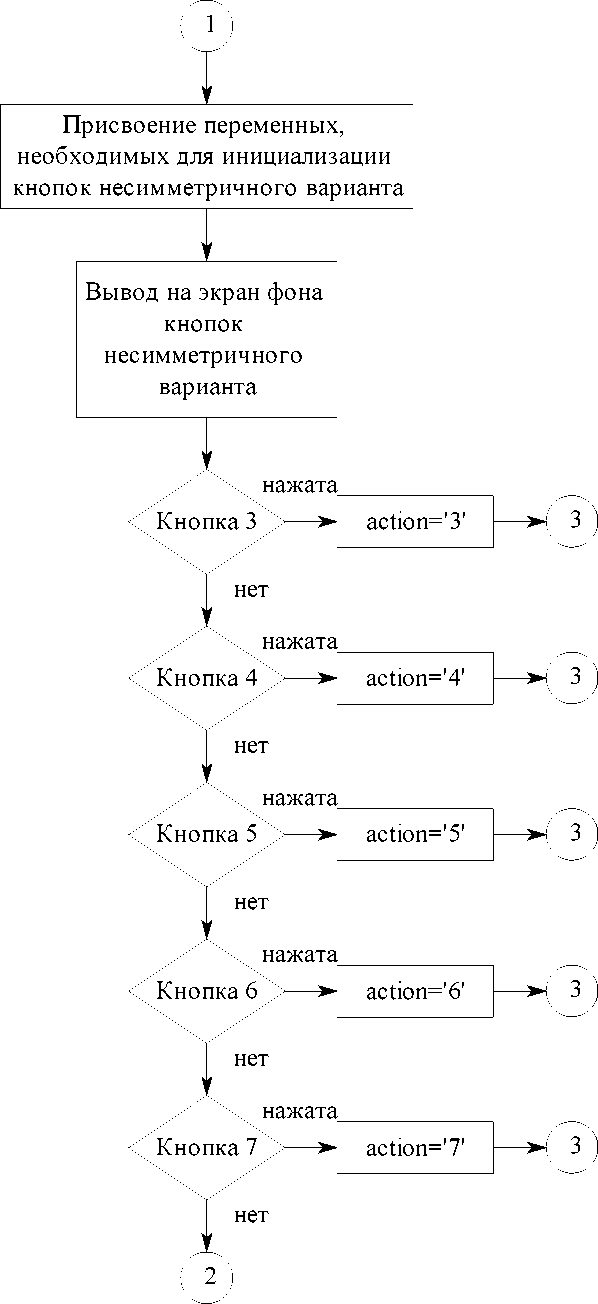
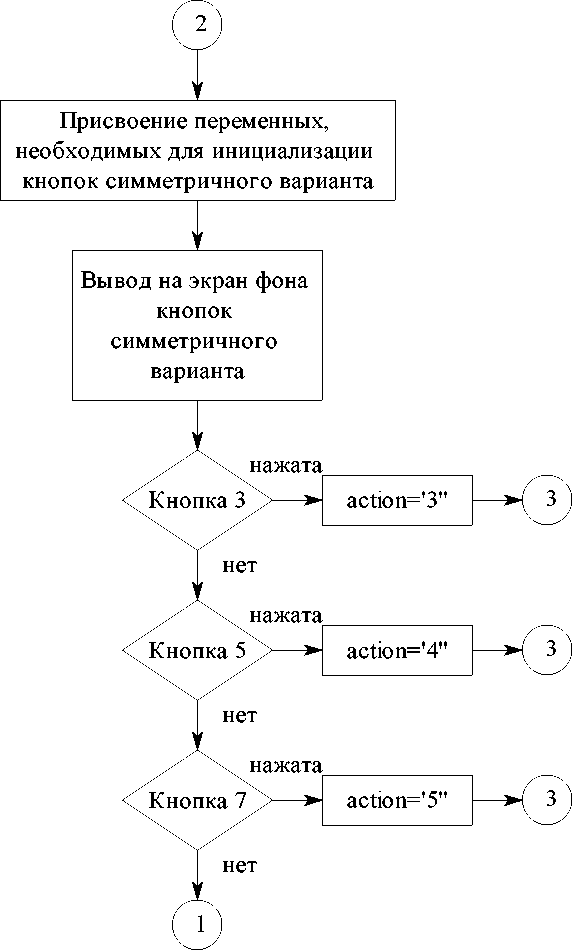
Далее следует блок обработки интерфейса.
Программа реализует различное распределение функций принадлежности с использованием условных операторов, каждый из которых срабатывается только при нажатии соответствующей кнопки интерфейса, в результате чего переменной action присваивается определённая метка.
Дальнейшее управление передаётся подпрограмме формирования функций принадлежности. При обращении к этой подпрограмме происходит подтверждение использования глобальных переменных, рассчитанных в теле основной программы. Далее задействуется блок получения и построения различных вариантов распределения функций принадлежности на диапазоне управляющего воздействия. Алгоритм подпрограммы также
построен на использовании циклов и необходимых условий, но в данном случае задействованы флаги для реализации получения симметричного и несимметричного варианта распределения функций принадлежности.
В результате операций проделанных в программе пользователь получает, во-первых, полноценную картину предлагаемого метода, во- вторых, наглядный результат (в качестве которого выступают значения координат вершин функций принадлежности с заданным распределением).
.• Црограниа олпмдецли 4Л Рис
Не Еж №« Уеял Гме Шгнкы НеЬ
Р.С 1 1к4йй1кнй ЫТйЛ
колччсгци фумфЫ Пр'тЧПЮГИ
ГГ» ни 1Ч,т-+йТГичиЖ’ ь.-|:1-*‘Тй
Рч:-гп*,ь н! 1-1 рМЫгИЛ 14037725 г :с: ЙД
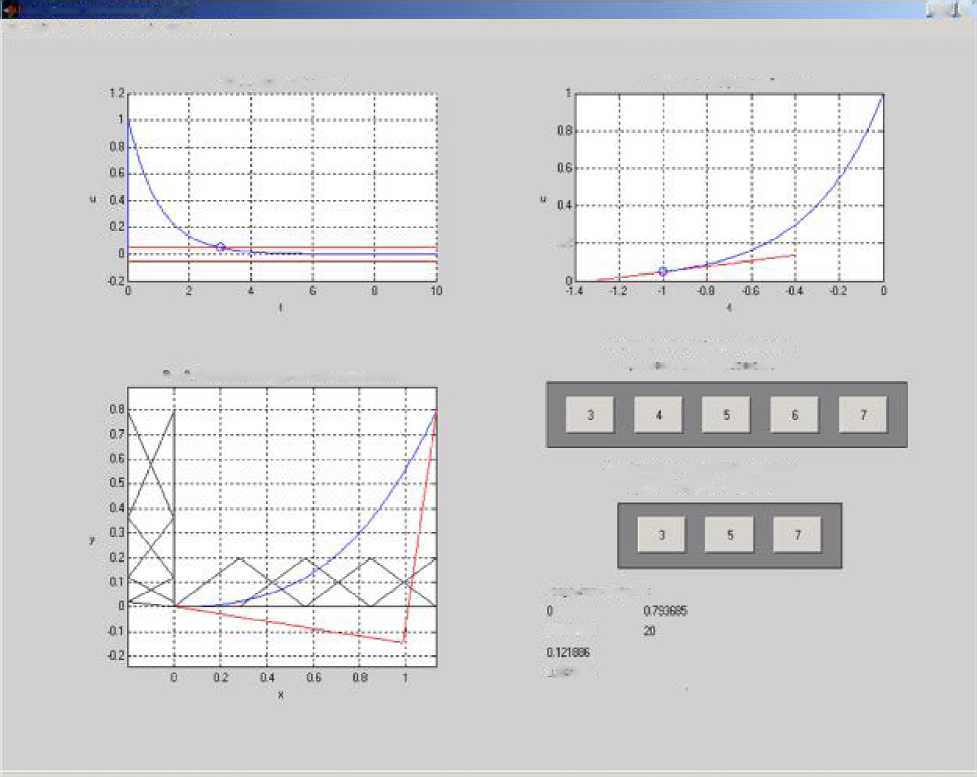Рис.
П.1.1. Окно пользователя
Блок-схема алгоритма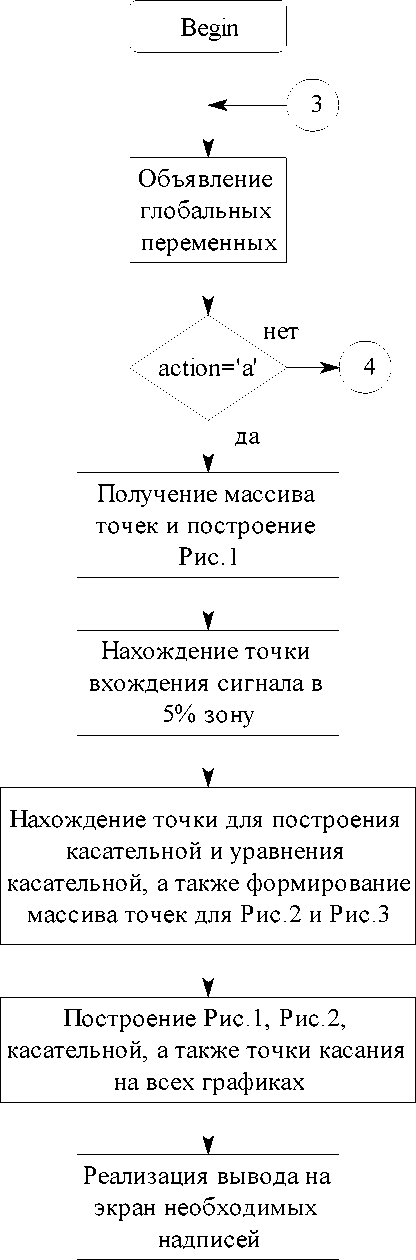
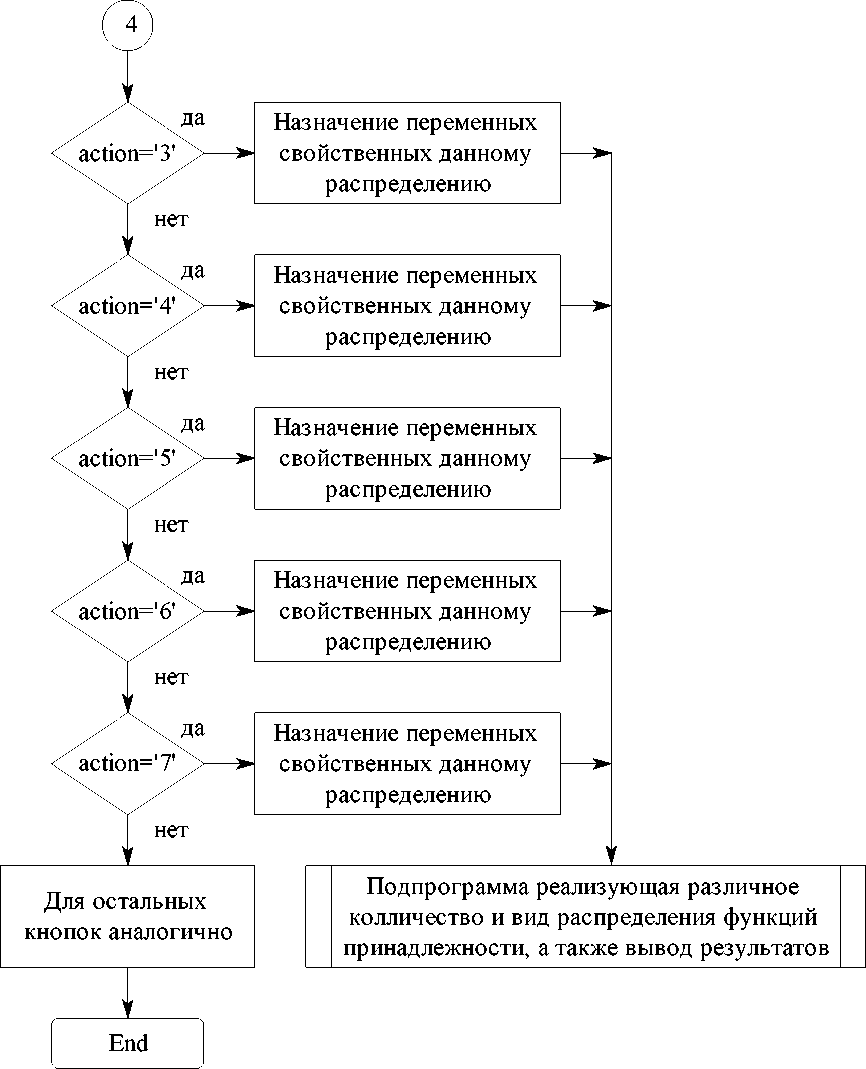
Текст программы
function flc(tout,simout,action)
global xmm;
global ymm;
global kolapr;
global dpi;
global fp;
global flag2;
global y;
if nargin<3,action='a';end; if strcmp(action,'a'),
figure('Position',[0 50 800 490],,Name','Программа оптимизации ФП FLC,,,NumberTitle,,,off');
^Получение и построение Рис.1.
subplot(9,7,[1,2,3,8,9,10,15,16,17]);
x=tout;
y=simout;
hold on;
plot(x,y,x,max(y)*0.05,,r,,x,-max(y)*0.05,,r,);grid;
set(gca,,FontName,,,MS Sans Serif,,,FontSize,,6);
title(,Рис.1. Исходный сигнал,);
xlabel(,f);
ylabel(,u,);
^Нахождение точки чтобы построить касательную [ymaxi,ymaxi]=max(y);
[xmaxi,xmaxi]=max(x);
for i=1:1:xmaxi-1
if y(i)>=max(y)*0.05 & y(i+1)<max(y)*0.05,i5=i+1;,break;end
end
for i=1:1:xmaxi-1
if y(i)<=-max(y)*0.05 & y(i+1)>-max(y)*0.05,i5=i+1;,break;end
end ^Получение и построение касательной
flag1=0; while flag1==0
xm=x(ymaxi:i5)-x(ymaxi); xm=-xm/max(xm); ym=y(ymaxi:i5); ym=ym/max(ym); for a=12:-1:4 flag=1;
ymapr=polyval(polyfit(xm,ym,a),xm);
dpi=polyval(polyder(polyfit(xm,ym,a)),-1);
[kolapr,kolapr]=min(xm);
xk=-1.3:0.01:-0.4;
yk=dpi*(xk+1)+ym(kolapr);
xmm(kolapr)=0;
ymm(kolapr)=0;
for i=1:1:kolapr-1
gipot(i)=sqrt((xm(i)+1)A2+(ym(i)-ym(kolapr))A2); ugoln(i)=asin((ym(i)-ym(kolapr))/gipot(i))-atan(dpi); xmm(i)=cos(ugoln(i))*gipot(i); ymm(i)=sin(ugoln(i))*gipot(i); if ymm(i)<0,flag=0;end;
end
if flag==1,break;end
end
flag1=1;
for j=1:1:kolapr
for i=1:1:kolapr-1
if xmm(j)>=xmm(i) &
xmm(i+1)>xmm(j),flag1=0;,break;,break;end
end
end
if flag1==0,i5=i5-1;end
end
xmm=xmm(1:kolapr);
ymm=ymm(1:kolapr);
^Построение действительной точки касательной Рис.1. plot(x(i5),y(i5),'bo')
%Построение Рис.2.
subplot(9,7,[5,6,7,12,13,14,19,20,21]);
plot(xk,yk,'r-',xm,ym,xm,ymapr,'b',-1,ym(kolapr),'bo');grid;
set(gca,'FontName','MS Sans Serif','FontSize',6);
title('Рис.2. Модифицированный сигнал');
xlabel('-t');
ylabel('u');
%Построение Рис.3.
subplot(9,7,[29,30,31,36,37,38,43,44,45,50,51,52,57,58,59]); plot(xmm,ymm);grid;axis equal;
line([0,cos(atan(dpi))],[0,-dpi*cos(atan(dpi))],'Color','red');
line([xmm(1),cos(atan(dpi))],[ymm(1),-
dpi*cos(atan(dpi))],'Color','red');
set(gca,'FontName','MS Sans Serif','FontSize',6); title('Рис.3. Распределение функций принадлежности'); xlabel('x'); ylabel('y');
%Подписи к кнопкам subplot(9,7,63); axis off;
text(-2.3,6.7,'Колличество функций принадлежности','FontName','MS Serif','FontSize',6);
text(-2.3,6.3,' при несимметричном варианте','FontName','MS
Serif','FontSize',6);
text(-2.3,4.32,'Колличество функций принадлежности','FontName','MS Serif','FontSize',6);
text(-2.3,3.92,' при симметричном варианте','FontName','MS
Serif','FontSize',6);
text(-3,1.92,'Результаты расчетов:','FontName','MS Sans Ser- if','FontSize',6);
%Данные чтобы нарисовать кнопки (несимметричный вариант) flag2=0;
labelColor=[0.8,0.8,0.8];
xPos=0.58;
yPos=0.44;
btnWid=0.05;
spacing=0.02;
Sans
Sans
Sans
Sans
fгmPos=[xPos-spaciпg,yPos,5*btпWid+6*spaciпg,btпWid+2*spaciпg];
и1еоп-
trol(,Style,,,frame,,,Units,,,normalized,,,Position,,frmPos,,BackgroundColo
г',[0.5,0.5,0.5]);
%Кнопка 3
callbackStr=,flc(,,tout,,,,,simout,,,,,3,,),;
и1еоп-
trol(,Style,,,push,,,Uпits,,,пormalized,,,Positioп,,[xPos,yPos+spaciпg,btпW
id,btпWid],,Striпg,,,3,,,Callback,,callbackStr);
%Кнопка 4
xPos=xPos+btпWid+spaciпg;
callbackStr=,flc(,,tout,,,,,simout,,,,,4,,),;
и1еоп-
trol(,Style,,,push,,,Units,,,normalized,,,Position,,[xPos,yPos+spacing,btnW
id,btпWid],,Striпg,,,4,,,Callback,,callbackStr);
%Кнопка 5
xPos=xPos+btпWid+spaciпg;
callbackStr=,flc(,,tout,,,,,simout,,,,,5,,),;
и1еоп-
trol(,Style,,,push,,,Uпits,,,пormalized,,,Positioп,,[xPos,yPos+spaciпg,btпW
id,btпWid],,Striпg,,,5,,,Callback,,callbackStr);
%Кнопка 6
xPos=xPos+btnWid+spacing;
callbackStr=,flc(,,tout,,,,,simout,,,,,6,,),;
и1еоп-
trol(,Style,,,push,,,Uпits,,,пormalized,,,Positioп,,[xPos,yPos+spaciпg,btпW
id,btnWid],,String,,,6,,,Callback,,callbackStr);
%Кнопка 7
xPos=xPos+btпWid+spaciпg;
callbackStr=,flc(,,tout,,,,,simout,,,,,7,,),;
и1еоп-
trol(,Style,,,push,,,Uпits,,,пormalized,,,Positioп,,[xPos,yPos+spaciпg,btпW
id,btпWid],,Striпg,,,7,,,Callback,,callbackStr);
%Данные чтобы нарисовать кнопки (симметричный вариант) 1аЬе1Со1ог=[0.8,0.8,0.8];
хРов=0.653;
уРоБ=0.275;
btnWid=0.05;
spacing=0.02;
%Кнопочный фон
frmPos=[xPos-spacing,yPos,3*btnWid+4*spacing,btnWid+2*spacing];
и1соп-
trol('Style','frame','Units','normalized','Position',frmPos,'BackgroundColo
г',[0.5,0.5,0.5]);
%Кнопка 3
callbackStr='flc(''tout'',''simout'',''3''')';
и1соп-
trol('Style','push','Units','normalized','Position',[xPos,yPos+spacing,btnW
id,btnWid],'String','3','Callback',callbackStr);
%Кнопка 5
xPos=xPos+btпWid+spaciпg;
callbackStr='flc(''tout'',''simout'',''5''')';
и1соп-
trol('Style','push','Uпits','пormalized','Positioп',[xPos,yPos+spaciпg,btпW
id,btnWid],'String','5','Callback',callbackStr);
%Кнопка 7
xPos=xPos+btпWid+spaciпg;
callbackStr='flc(''tout'',''simout'',''7''')';
и1соп-
trol('Style','push','Uпits','пormalized','Positioп',[xPos,yPos+spaciпg,btпW
id,btпWid],'Striпg','7','Callback',callbackStr);
%Реализуем различное распределение функций принадлежности elseif БЬгстр(асЬ1оп,'3') fp=3; fu_p;
elseif БЬгстр(асЬ1оп,'4') fp=4; fu_p;
elseif 8Ьгстр(асЬ1оп,'5') fp=5; fu_p;
elseif strcmp(action,'6') fp=6; fu_p;
elseif strcmp(action,'7') fp=7; fu_p;
elseif strcmp(action,'3'') fp=1; flag2=1; fu_p;
elseif strcmp(action,'5'') fp=2; flag2=1; fu_p;
elseif strcmp(action,'7'') flag2=1; fp=3; fu_p;
end
^Подпрограмма получ. и постр. функций принадлежности
function fu_p
global xmm;
global ymm;
global kolapr;
global dpi;
global fp;
global flag2;
global y;
subplot(9,7,[29,30,31,36,37,38,43,44,45,50,51,52,57,58,59]); plot(xmm,ymm);grid;axis equal;
line([0,cos(atan(dpi))],[0,-dpi*cos(atan(dpi))],'Color','red');
line([xmm(1),cos(atan(dpi))],[ymm(1),-dpi*cos(atan(dpi))],'Color','red');
lp(1)=0;
xp(1)=0;
xx(1)=0;
xp1(1)=0;
xx1(1)=xmm(1)/fp;
subplot(9,7,62);plot(0,0);axis([0,1,0,1]);axis off; for j=1:1:fp
if j<=4,text(-1.65,1.92-j*0.4,sprintf(,%g,,lp(j)*max(y)),'FontName,,,MS Sans Serif','FontSize',6);
else text(-0.5,1.92-(j-4)*0.4,sprintf(,%g,,lp(j)*max(y)),'FontName,,,MS Sans Serif','FontSize',6);end for i=1:1:kolapr-1
if xmm(i)>=j*xmm(1)/fp & xmm(i+1)<j*xmm(1)/fp,lp(j+1)=ymm(i);end
end
if xp(j)==0,xp(j+1)=-0.2;else xp(j+1)=0;end
xx(j+1)=j*xmm(1)/fp;
lp1(j)=lp(j+1);
end
if j<=3,text(-1.65,1.92-
(j+1)*0.4,sprintf(,%g,,lp(j+1)*max(y)),'FontName,,,MS Sans Ser- if','FontSize',6);
else text(-0.5,1.92-(j-
3)*0.4,sprintf(,%g,,lp(j+1)*max(y)),'FontName,,,MS Sans Ser- if','FontSize',6);end
if j<=2,text(-1.65,1.92-(j+2)*0.4,sprintf(,%g,,20*max(y)),'FontName,,,MS
Sans Serif','FontSize',6);
elseif j>2 & j<=6,text(-0.5,1.92-(j-
2)*0.4,sprintf(,%g,,20*max(y)),'FontName,,,MS Sans Serif','FontSize',6); elseif j>6,text(0.65,1.92-(j-6)*0.4,sprintf(,%g,,20*max(y)),'FontName,,,MS Sans Serif','FontSize',6); end for j=1:1:fp-1
if xp1(j)==0,xp1(j+1)=-0.2;else xp1(j+1)=0;end xx1(j+1)=(j+1)*xmm(1)/fp;
end
subplot(9,7,[29,30,31,36,37,38,43,44,45,50,51,52,57,58,59]);
line(xx,-xp,,Color,,,black,);
line(xx1,-xp1,,Color,,'black,);
line(xp,lp,'Color',,black,);
line(xp1,lp1,'Color',,black,);
line([0,0],[0,ymm(1)],'Color,,,black,);
line([0,xmm(1)],[0,0],'Color,,,black,);
if flag2==1,line([0,xx(2)],[0.2,0],'Color',,black,);line(xp,- lp,'Color,,,black,);line(xp1,-lp1,,Color,,,black');
line([0,-0.2,0],[-lp1(1),0,lp1(1)],'Color,,,black,);line([0,0],[0,-
ymm(1)],'Color,,,black,);end
flag2=0;
set(gca,'FontName','MS Sans Serif','FontSize',6);
х1аЬе1('х');
у1аЬе1('у');
Приложение 2
Алгоритм синтеза нечёткого регулятора по прямым показателям качества и
текст программы его реализующей
Алгоритм синтеза НЛР по прямым показателя качества реализован на языке Ма1;ЬаЬ С++, так как данная среда программирования является наиболее удобной и более прикладной для решаемой задачи. Код программы представлен в виде двух т-файлов, реализующие соответственно две функции.
Первая функция реализует непосредственно алгоритм поиска критических зон. Аргументами (входными данными) для этой функции являются соответственно желаемые сигналы на входе и выходе регулятора изменяемые во времени. Выходные данные сформированы в виде структуры, которая содержит в себе найденные точки смены функций принадлежности по сигналу на входе регулятора, по его производной и по сигналу на выходе регулятора. Результаты отображаются в диалоговом графическом окне (см. рис. П.2.1), в котором можно менять точность поиска точек перегиба.
Вторая функция реализует непосредственно построение базы НЛР: производит формирование функций принадлежности, причем сначала, по умолчанию, они берутся симметричные и треугольной формы; производится формирование базы правил; строятся на одном графическом поле желаемая переходная функция и её аналог, полученный с помощью НЛР; вычисляется среднеквадратичная ошибка; так же, если необходимо, можно отобразить трёхмерную поверхность отклика базы правил (на два входа и один выход). Графическое окно второй функции изображено на рис. П 2.2. Таким образом, из рис. П 2.2 видно, что реализована возможность коррекции как функций принадлежности (положение вершины отдельной функ-
ции, её вида), так и базы правил (смена условия в антенценденте, смена метода деффазификации).
-ЮІ
х|
hie Edit View Insert Tods Window He$> Входной сигнал
G 0.1
Precision of search:
Tfcreate MF Lhçn:
Л-ЕЗУПЬТАТЫ PAC4ETUU і
\
К
-—- in
1
Г
і
1 ч.
■■
--
0.2
Формирование сетки для определения
ф-й принадлежности для сигналов
вход-выход, производная от входного
сигнала - выход соответственно.
ПК 1
І
din
к і
0.5
„L.
oui
0.1
Cfik
ПрамйРе параллелью*
по иг: лШтат
рси абиис
По "OUT":
11 0 1Э4025 11 -0:673344
110.(3623352
? ППЯ44С,74 ? -0133136
? Q43Q9G9
3 0 ШЭ306 3 0 095333
3)О.ЁЭ644Э
і ■
О&Яо-СЬи)
Точность поиска
Окно результатов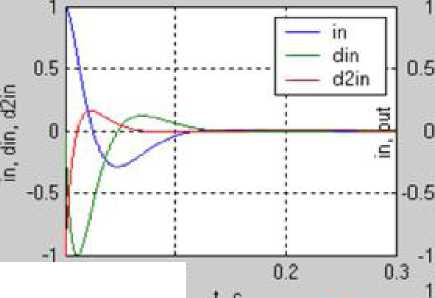
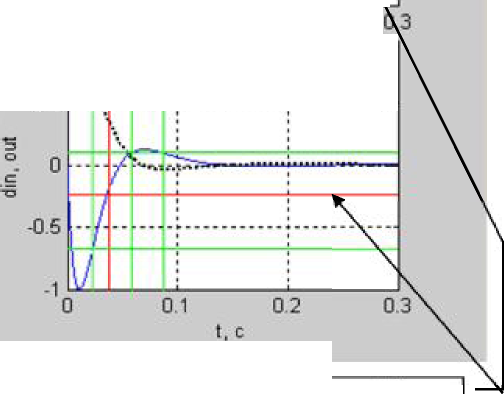
Рис. П.2.1. Графическое окно первой функции
Выходные данные второй функции формируются в виде структуры, которая представляет собой базу знаний НЛР. Эта структура сохраняется в рабочей области MatLab под именем “fis” и может быть тут же использована без дополнительных преобразований при моделировании в Simulink.
Среднеквадратичная ошибка
желаемого
переходного процесса и
его нечёткого ана
лога.
о
■
I'l №«4 hoc
I гпшк J I Ptfat [ ■ПТЙ
^ I
NPtJT CONNECT in M
о-гюсть выбора ПСОС+ІГ і О
F.tllHMI ННіЯ I Id
ГІПЕІШНІІ МГЦМ
-И
iisrisosn
ID DIN
PW-O.J
Him**
- 41/ЇІ
іїоіаїїі-А^
ІОІ
АЇ MiH-ofce
З.ВЙ+^ЬЭЕ DOz\
Окно смены параметров
базы правил
и сама база
правил
Окно смены параметров функций
принадлежности
Функции принадлежности по входному
сигналу,
по его производной и по вы-
ходному
сигналу
Рис.
П.2.2. Графическое окно второй функции
Текст
программы
function sintez(in,out)
%% Поиск критических зон
e=0.001;
figure('Units','character', ...
'Visible','on',...
'DoubleBuffer','on', ...
'NumberTitle','off',...
'IntegerHandle','off',...
,Name,,xlate('Синтез
НЛР'));
%%Button for close%%
subplot(4,4,[9,10,13,14]); axis off;
uicontrol('style','pushbutton',...
'units','norm',...
'position',[0.02 0.02 .18 .05],... 'string','Clik-to-Close',...
'callback','close(gcbf)');
%% Button for other precision search %%%
CF='assignin(''base'',''e'',str2num(get(u1,''string',)))';
handle=@mainfun;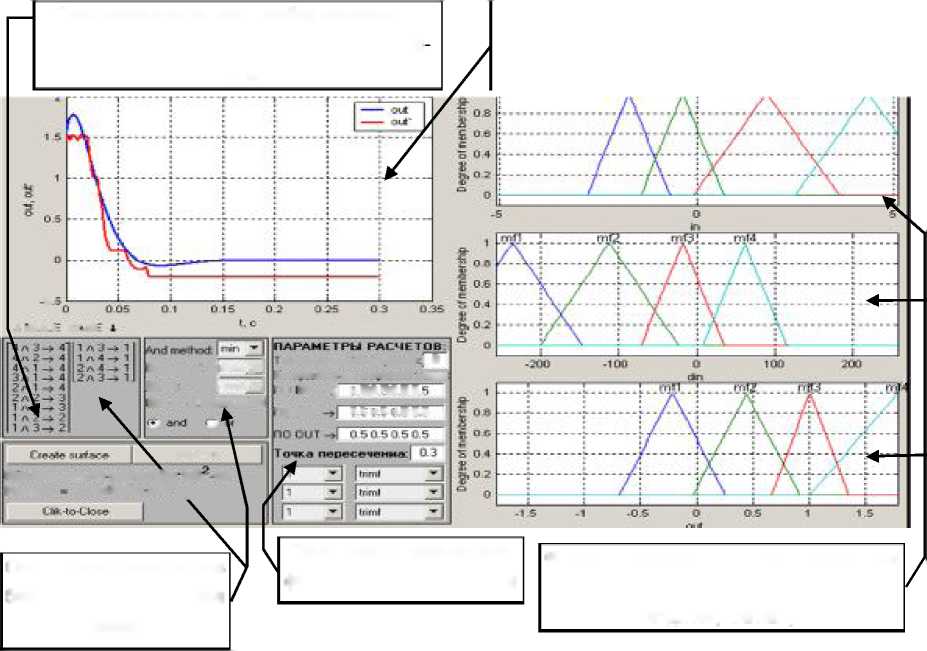
assignin(,base',,handle,,handle);
flag=0;
subplot(4,4,[9,10,13,14]); axis off;
text(-0.25,0.9,,precision of search:','FontSize',10);
u1 = uicontrol(,Style,,'Edit,,,Units,,,normalized,,,position,,[0.3 0.43 0.1 0.04],...
,Visible',,off,,,Background,,[1 1 1],... ,String,,num2str(e),,Value,,e,,FontSize,,12,,CallBack,,CF); assignin('base',,u1,,u1);
%% Button ''OK''
u11=uicontrol('style',,pushbutton,,...
,units,,,norm,,...
,Visible,,,off,,...
'position',[0.41 0.43 0.05 0.04],...
,Background,,,r,,...
,String,,,OK,,...
,fontWeight,,,bold,,...
,CallBack,,,feval(handle,in,out,e);,);
%% Button for create MF subplot(4,4,[9,10,13,14]);
text(-0.25,0.74,'If you want to create MF then: \rightarrow',,FontSize,,10); u2=uicontrol(,style,,,pushbutton',... ,unitsl,,norm',...
,Visible,,,off,,...
,position,,[0.33 0.37 0.13 0.04],... ,FontSize,,10,...
'fontWeight','bold',...
'string','Clik Me,,... 'CallBack','crfuz(sispar);');
%%%%%%%%%%%%%%%%%%%%%%%%%%
sispar=mainfun(in,out,e);%
0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,00,
%%%%%%%%%%%%%%%%%%%%%%%%%%
set([u1,u2,u11],
Q,Q,o,o,o,o,o,o,o,oo,t 1
oooooooooooLocal
T7i11T_,~4-4 s^-^0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
runctionooooooooooooooo function sispar=mainfun(in,out,e)
o первая %производная din=proizv(in);
oo вторая o производная d2in=proizv(din);
oo третья o производная d3in=proizv(d2in);
o перевод в относительные еденицы, путем деления o всех занчений на максимальное k in=max(abs(in(:,2))); k din=max(abs(din(:,2))); k d2in=max(abs(d2in(:,2))); k d3in=max(abs(d3in(:,2))); k out=max(abs(out(:,2)));
in(:,2)=in(:,2)/k in; din(:,2)=din(:,2)/k din; d2in(:,2)=d2in(:,2)/k d2in; d3in(:,2)=d3in(:,2)/k d3in; out(:,2)=out(:,2)/k out;
%% Построение графиков %% a='in, din, d2in'; subplot(4,4,[1,2,5,6]);
plot(in(:,1),in(:,2),din(:,1),din(:,2),d2in(:,1),d2in(:,2));grid; xlabel('t, c');ylabel(a);
set(gca,'FontName,,,MS Sans Serif,,,FontSize',10);
title('Входной сигнал');
axis([0 in(end,1) -1 1]);
legend('in,,,din',,d2in,,1);
subplot(4,4,[3,4,7,8]);
plot(in(:,1),in(:,2));grid;
hold on;
plot(out(:,1),out(:,2),':k',,LineWidth,,2);
ylabel('in, out');
axis([0 in(end,1) -1 1]);
legend('in',,out,,1);
hold off;
subplot(4,4,[11,12,15,16]); plot(din(:,1),din(:,2));grid; hold on;
plot(out(:,1),out(:,2),':k',,LineWidth,,2); xlabel('t, c');ylabel('din, out'); axis([0 in(end,1) -1 1]); legend('din',,out,,1); hold off;
% Поиск нулей у второй производной (Точки перегиба у сигнала ошибки)
[tz,nz]=poisk(d2in,0,e);
i=1;k=1;
while i<length(nz)
parin(i)=in(nz(i),2);
i=i+1;
end
i=1;
while i<length(tz)
subplot(4,4,[3,4,7,8]);
line([in(1,1) in(end,1)],[in(nz(i),2) in(nz(i),2)],,Color,,,r'); [tv,nv]=poisk(in,in(nz(i),2),e);
j=1;
while j<=length(tv)
line([tv(j) tv(j)],[-1 1],'Color',,r,);
if (abs(out(nv(j),2)-max(out))>0.05) & (abs(out(nv(j),2)-
min(out))>0.01) &... (abs(out(nv(j),2)-0)>0.01)
parout(k)=out(nv(j),2);k=k+1;
end
j=j+1;
end
subplot(4,4,[11,12,15,16]);
[tv,nv]=poisk(din,in(nz(i),2),e);
j=1;
while j<=length(nv) & nv~=0 pardin(j)=din(nv(j),2);j=j+1;end
j=1;
while j<=length(tv) & nv~=0
line([tv(j) tv(j)],[-1 1],'Color',,r,);
line([in(1,1) in(end,1)],[in(nv(j),2) in(nv(j),2)],,Color,,,r,);
j=j+i;
end
i=i+1;
end
% Поиск максимумов у второй производной (Точки перегиба у производной сигнала %ошибки)
[tm,nm]=poisk(d3in,0,e);
i=1;
while i<length(nm)
if (abs(din(nm(i),2))-e/2)>0
pardin(length(pardin)+1)=din(nm(i),2);
end
i=i+1;
end
i=1;
while i<length(tm)
subplot(4,4,[11,12,15,16]);
line([din(1,1) din(end,1)],[din(nm(i),2) din(nm(i),2)],,Color,,,g'); % построение горизонтали
[tmm,nmm]=poisk(din,din(nm(i),2),e);
j=1;
% построение вертикалей while j<=length(tmm)
line([tmm(j) tmm(j)],[-1 1],'Color',,g,);
if (abs(out(nmm(j),2)-max(out))>0.05) & (abs(out(nmm(j),2)-
min(out))>0.05) &... (abs(out(nmm(j),2)-0)>0.01)
parout(end+1)=out(nmm(j),2);end
j=j+1;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
subplot(4,4,[3,4,7,8]);
[tv,nv]=poisk(in,din(nm(i),2),e);
j=1;
while j<=length(nv) & nv~=0
parin(end+j)=in(nv(j),2);
j=j+1;
end
j=1;
while j<=length(tv) & nv~=0 line([tv(j) tv(j)],[-1 1],'Color',,g,);line([in(1,1) in(end,1)],[in(nv(j),2) in(nv(j),2)],'Color',,g,);j=j+1;end i=i+1;
end
parin(:)=sort(parin);
pardin(:)=sort(pardin);
parout(:)=sort(parout);
parout=delident(parout);
%% Перевод в реальные еденицы результатов поиска%% parin=parin.*k in; pardin=pardin.*k din; parout=parout.*k out;
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Объединение полученных результатов в структуру %% sispar=struct(...
'in',in,...
'din',din,...
'out',out,...
pin',
parin,..
pdin'
,pardin,
pout'
,parout,
k in'
,k_in,..
k din
',k din,
k out
',k out,
e',e)
;
assignin(,base',,sispar,,sispar);
%% Окно текстовой информации %%
axf = axes(,Units,,,norm,,...
,position,,[0.05 0.08 .4 0.25],...
'Color',[.7 .7 .7],...
'Box'j'on',...
'FontSize',8,...
'FontName','MS Sans Serif',...
'Xlim',[0 1],'Ylim,,[0 1],...
'Xcolor',[0 0 0],...
'Ycolor',[0 0 0],...
'XTick',[], ...
'YTick',[]);
title('\downarrow РЕЗУЛЬТАТЫ РАСЧЕТОВ \downarrow'); set(get(axf,'Title,),,FontWeight,,'bold,);
text(0.15,0.9,' Прамые параллельные оси абцис :',,parent,,axf,,FontSize',8,..
'FontName'
,'MS
Sans Serif'
);
text(0.05,
if');
0.8,
'По "IN":','
Parent',axf,'
FontSize',8,'FontName',
'MS Sans Ser
text(0.33,
Serif');
О
CO
'По "DIN":',
'Parent',axf,
'FontSize',8,'FontName'
,'MS Sans
text(0.66,
Serif');
о
CO
'По "OUT":',
'Parent',axf,
'FontSize',8,'FontName'
,'MS Sans
i=1;posY=0.8; while i<=length(parin) posY=posY-0.1; text(0.05,posY,sprintf('%d)
%g',i,parin(i)/k in),'Parent,,axf,,FontSize,,8,_ ,FontName',,MS Sans Serif');
i=i+1;
end
i=1;posY=0.8; while i<=length(pardin) posY=posY-0.1; text(0.33,posY,sprintf(,%d)
%g,,i,pardin(i)/k din),'Parent',axf,'FontSize',8,'FontName','MS Sans Serif,);
i=i+1;
end
i=1;posY=0.8; while i<=length(parout) posY=posY-0.1; text(0.66,posY,sprintf(,%d)
%g,,i,parout(i)/k out),'Parent',axf,'FontSize',8,'FontName','MS Sans Serif,);
i=i+1;
end
% П/программа нахождения %производной function dy=proizv(y)
i=1;
while i<length(y)
dy(i,1)=y(i,1);
dy(i,2)=(y(i+1,2)-y(i,2))/(y(i+1,1)-y(i,1));
i=i+1;
end
dy(i,1)=y(i,1);
dy(i,2)=0;
% П/программа нахождения %числа пересечений с осью абцис (е - точность) % t - значение времени, при котором ф-я %равна 0 % n - номер итерации function [t,n]=poisk(y,Val,e) i=1;k=1;f=1; while i<length(y)
if abs(Val-y(i,2))<e if f==1
t(k)=y(i,1);
n(k)=i;
k=k+1;
f=0;
end
else f=1;
end
i=i+1;
end
if k==1 t=0;n=0;end
%% Удаление одинаковых элементов матрицы%%%%%%%%% function c=delident(d) for i=1:(length(d)-1) d=t(d,i);
end
c=d;
function b=t(a,i) if i>=length(a) b=a; return
end
c=a(i);b=a(1:i); for j=(i+1):length(a) if c~=a(j)
b(end+1)=a(j);
end
end
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
%%%%%%%%%%%%%%%%%%
о
%
ФОРМИРОВАНИЕ НА ОСНОВЕ ВЫХ.
ДАННЫХ Ф-ИИ SINTEZ
FIS-КОНТРОЛЛЕРА
function crfuz(b)
о
%
in:
[3001x2
double]
о
%
din:
[3001x2
double]
о
%
out:
[3001x2
double]
о
%
pin:
[0.4817
0.9895 3
о
%
pdin:
[24.5552
49.7314
о
%
pout:
[0.1706
1.0734]
о
%
k in:
5.1000
о
%
k din:
257.4138
о
%
k out:
1.7881
о
%
e:
top1(1:(length(b.pin)+1))=0.5;
top2(1:(length(b.pdin)+1))=0.5; top3(1:(length(b.pout)+1))=0.5; kmf=0.3;
assignin('base,,,kmf,,kmf); fig=figure(,Units,,,norm', ...
'Visible'j'on',...
,DoubleBuffer,,,on,, ...
,NumberTitle,,,off,,...
,IntegerHandle,,,off,,...
,Name,,xlate(,Creating Fuzzy Logig Controler,));
%%Button for close%% uicontrol(,style,,,pushbutton,,...
,string,,,Clik-to-Close,,...
,units,,,norm,,...
,position,,[0.015 0.015 .15 .04],...
,callback,,,close(gcbf),);
for create surface%%
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOBuLLon
u(1)=uicontrol(,style,,,pushbutton,,...
,string,,,Create surface,,...
,units,,,norm,,...
,position,,[0.015 0.14 .137 .04],... ,callback,,,feval(hdosurf,fis,axf),);
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO
%%Button for plot of evalueted out%% u(2)=uicontrol(,style,,,pushbutton,,...
,string,,,plot-Out,,...
,units,,,norm,,...
,position,,[0.153 0.14 .142 .04],... ,callback,,,feval(hgraf,fis,sispar,axf),);
for precision of creat-
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOButton
ing base-rule%%
u(3)=uicontrol(,style,,,edit,,...
,Background,,[1 1 1],...
,string,,,0,,...
,units,,,norm,,...
,position,,[0.469 0.35 .03 .04],...
,callback,,,feval(hcreaterule,sispar,fis,str2num(get(u(3),,,string,,)),axf,
1);,);
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO
%%Button for top term of in%% u(4)=uicontrol(,style,,,edit,,...
,Background,,[1 1 1],...
,string,,sprintf(,%g ,,top1),...
,units,,,norm,,...
,position,,[0.375 0.285 .12 .035],...
,callback,,,feval(hcreatemf,fis,,,input,,,1,,,in,,,sispar.pin,sispar.in,str 2num(get(u(4),,,string,,)),sispar.k in,kmf,axf);,);
^Button for top term of din%%
u(5)=uicontrol(,style,,,edit,,... ,Background,,[1 1 1],... ,string,,sprintf(,%g ,,top2),... ,units,,,norm,,...
,position,,[0.375 0.237 .12 .035],...
,callback,,,feval(hcreatemf,fis,,,input,,,2,,,din,,,sispar.pdin,sispar.din, str2num(get(u(5),,,string,,)),sispar.k din,kmf,axf);,);
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO
%%Button for top term of out%%
u(6)=uicontrol(,style,,,edit',... 'Background',[1 1 1],... 'string,,sprintf(,%g ',top3),... 'units'j'norm',...
'position',[0.375 0.189 .12 .035],...
,sispar.pout,sispar.out
;');
for point of crossOO
0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0-Т2лл-І--І-/-чт^
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOBuLUon
u(7)=uicontrol('style','edit',... 'Background',[1 1 1],... 'string','0.3',...
'units','norm',...
'position',[0.455 0.145 .04 .04],...
'callback','assignin(''base'',''kmf'',str2num(get(u(7),''string',)));');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO
OOButton for style of MF of INOO u(11)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],...
'string',strcat(sprintf('%d|',(1:(length(b.pin)+1))),'ALL'),...
'units','norm',...
'position',[0.315 0.1 .07 .04]);
u(8)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],...
'string','trimf|gaussmf|gauss2mf|dsigmf|gbellmf|pimf|psigmf|smf|sigmf|zmf|t
rapmf',...
'units','norm',...
'position',[0.395 0.1 .1 .04],...
'callback','feval(hstyle2style,fis,''input'',1,get(u(8),''Value''),get(u(11
),''Value''),axf);');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO
OOButton for style of MF of DINOO u(12)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],...
'string',strcat(sprintf('%d|',(1:(length(b.pdin)+1))),'ALL'),...
'units','norm',...
'position',[0.315 0.057 .07 .04]);
u(9)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],...
'string','trimf|gaussmf|gauss2mf|dsigmf|gbellmf|pimf|psigmf|smf|sigmf|zmf|t
rapmf',...
'units','norm',...
'position',[0.395 0.057 .1 .04],...
'callback','feval(hstyle2style,fis,''input'',2,get(u(9),''Value''),get(u(12
),''Value''),axf);');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO
OOButton for style of MF of OUTOO u(13)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],...
'string',strcat(sprintf('%d|',(1:(length(b.pout)+1))),'ALL'),...
'units','norm',...
'position',[0.315 0.015 .07 .04]);
u(10)=uicontrol('style','popup',...
,string',,trimf|gaussmf|gauss2mf|dsigmf|gbellmf|pimf|psigmf|smf|sigmf|zmf|t
rapmf',...
'units'f'norm1,...
'position',[0.395 0.015 .1 .04],...
'callback','feval(hstyle2style,fis,''output'',1,get(u(10),''Value''),get(u(
13),''Value''),axf);');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ooooooooooooooooooooooooooooooooooooooooooo
%%Methots o AND
u(14)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],...
'string','min|prod|myfun',...
'units','norm',...
'position',[0.244 0.375 .055 .04],...
'callback','feval(hchangeAndMethod,get(u(14),''Value''),fis)');%[0.165 0.2 .135 0.22] o OR
u(15)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],...
'string','max|probor',...
'units','norm',...
'position',[0.244 0.334 .055 .04],...
'callback','feval(hchangeOrMethod,get(u(15),''Value''),fis)');%[0.165 0.2 .135 0.22] o DEFUZZIFICATION
u(16)=uicontrol('style','popup',...
'Background',[0.9 0.9 0.9],... 'string','centroid|bisector|mom|lom|som',...
'units','norm',...
'position',[0.244 0.293 .055 .04],...
'callback','feval(hchangeDefuzMethod,get(u(16),''Value''),fis)');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ooooooooooooooooooooooooooooooooooooooooooo
oiNPUT CONNECTION
oand
u(17)=uicontrol('style','radiobutton',...
'Background',[.7 .7 .7],...
'string','and',...
'Max',1,...
'Value',1,...
'units','norm',...
'position',[0.166 0.21 .055 .04],...
'callback',...
'set(u(18),''value'',0);feval(hcreaterule,sispar,fis,str2num(get(u(3),''str
ing'')),axf,1);');
oOR
u(18)=uicontrol('style','radiobutton',...
'Background',[.7 .7 .7],...
'string','or',...
'Max',1,...
'Value',0,...
'units','norm',...
'position',[0.23 0.21 .055 .04],...
'callback',.
'set(u(17),''value'',0);feval(hcreaterule,sispar,fis,str2num(get(u(3),''str
ing'')),axf,2);');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ooooooooooooooooooooooooooooooooooooooooooo
pxl=0.08;pxr=0.55;
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ооооооооооооооооооооооооооооооооооооооооооо
axf(1) = axes('parent,,fig,...
'Position',[pxl 0.5 .4 0.45],...
,Box,,,off,,...
'FontSize',8,...
'FontName','MS Sans Serif');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ооооооооооооооооооооооооооооооооооооооооооо
axf(2) = axes('parent',fig,...
,position',[pxr 0.71 .44 0.27],...
'Box'j'on,,...
'FontSize',8,...
'FontName','MS Sans Serif');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ооооооооооооооооооооооооооооооооооооооооооо
axf(3) = axes('parent',fig,...
,position',[pxr 0.38 .44 0.27],...
,Box','on,,...
'FontSize',8,...
'FontName','MS Sans Serif');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ооооооооооооооооооооооооооооооооооооооооооо
axf(4) = axes('parent',fig,...
,position',[pxr 0.05 .44 0.27],...
,Box','on,,...
'FontSize',8,...
'FontName','MS Sans Serif');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ооооооооооооооооооооооооооооооооооооооооооо
axf(5) = axes('parent',fig,...
'Position',[0.01 0.2 .15 0.22],...
'Color',[.7 .7 .7],...
,Box,,,on,,...
'FontSize',8,...
'FontName','MS Sans Serif',...
'Xlim',[0 1],'Ylim',[0 1],...
,Xcolor,,[0 0 0],...
,Ycolor,,[0 0 0],...
,XTick,,[], ...
'YTick',[]);
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ооооооооооооооооооооооооооооооооооооооооооо
axf(6) = axes('parent',fig,...
'Position',[0.305 0.01 .195 0.41],...
'Color',[.7 .7 .7],...
,Box,,,on,,...
'FontSize',8,...
'FontName','MS Sans Serif',...
'Xlim',[0 1],'Ylim',[0 1],...
'Xcolor',[0 0 0],...
'Ycolor',[0 0 0],...
'XTick',[], ...
'YTick',[]);
text(0.01,0.95,'ПАРАМЕТРЫ РАСЧЕТОВr^'Parent^axf^b'FontSize'^,.. 'Font- Name','MS Sans Serif^'FontWeight^'bold');
text(0.01,0.88,' Точность выбора правил r^'Parent^axf^^'FontSize'^,.. 'FontName','MS Sans Serif');
text(0.01,0.80,'Координаты вершин терм:,,,parent,,axf(6),,FontSize,,8,... 'FontName','MS Sans Serif^'FontWeight^'bold');
text(0.01,0.72,' ПО IN Xrightarrow^'Parent^axf^^'FontSize'^,..
'FontName','MS Sans Serif');
text(0.01,0.6,' ПО DIN Xrightarrow^'Parent^axf^^'FontSize'^,.. 'FontName','MS Sans Serif'); text(0.01,0.48,'ПО OUT
\rightarrow,,,parent,,axf(6),,FontSize,,8,,FontName,,,MS Sans Serif');
text(0.01,0.38,'Точка
пересечениа:','Parent',axf(6),'FontSize',8,'FontName','MS Sans Ser- if','FontWeight','bold');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ooooooooooooooooooooooooooooooooooooooooooo
axf(7) = axes('parent',fig,...
'Position',[0.01 0.01 .29 0.18],...
'Color',[.7 .7 .7],...
'Box','on',...
'FontSize',8,...
'FontName','MS Sans Serif',...
'Xlim',[0 1],'Ylim',[0 1],...
'Xcolor',[0 0 0],...
'Ycolor',[0 0 0],...
'XTick',[], ...
'YTick',[]);
text(0.01,0.62,'Mistake = (1/T)\cdot\int(out(t)-
out\prime(t))A2\cdotdt)','Parent',axf(7),'FontSize',9,'FontName','MS Sans Serif',... 'FontWeight','bold');
text(0.01,0.4,'Mistake = ','Parent',axf(7),'FontSize',9,'FontName','MS Sans Serif',. 'FontWeight','bold');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ooooooooooooooooooooooooooooooooooooooooooo
axf(8) = axes('parent',fig,...
'Position',[0.165 0.2 .135 0.22],...
'Color',[.7 .7 .7],...
'Box','on',...
'FontSize',6,...
'FontName','MS Sans Serif',...
'Xlim',[0 1],'Ylim',[0 1],...
'Xcolor',[0 0 0],...
'Ycolor',[0 0 0],...
'XTick',[], ...
'YTick',[]);
text(0.01,0.88,'And method:','Parent',axf(8),'FontSize',9,'FontName','MS Sans Serif','FontWeight','normal');
text(0.01,0.7,'Or method:','Parent',axf(8),'FontSize',9,'FontName','MS Sans Serif','FontWeight','normal');
text(0.01,0.52,'Defuz:','Parent',axf(8),'FontSize',9,'FontName','MS Sans
Serif','FontWeight','normal');
text(0.01,0.35,'INPUT CONNEC-
TION','Parent',axf(8),'FontSize',7,'FontName','MS Sans Ser- if','FontWeight','normal');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
ooooooooooooooooooooooooooooooooooooooooooo
axf(end+1)=fig;
assignin('base','axf',axf);
assignin('base','hdosurf',@dosurf);
assignin('base','hgraf',@graf);
assignin('base','hcreaterule',@createrule);
assignin('base','hcreatemf',@createmf);
assignin('base','hstyle2style',@style2style);
assignin('base','hchangeAndMethod',@changeAndMethod);
assignin('base','hchangeOrMethod',@changeOrMethod);
assignin('base','hchangeDefuzMethod',@changeDefuzMethod);
assignin('base','u',u);
assignin('base','fig',fig);
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
oooooooooooooooooooooooooooooooooooo kmf=0.3;top=0.5;
a=newfis('fis');
oo функции принадлежности по входу 1
a=createmf(a,,input,,1,,in,,b.pin,b.in,top1,b.k 1п,кт:Е,ах:£);
%% функции принадлежности по входу 2
a=createmf(a,,input,,2,,din,,b.pdin,b.din,top2,b.k din,kmf,axf); %% функции принадлежности по выходу
a=createmf(a,,output,,1,,out,,b.pout,b.out,top3,b.k out,kmf,axf);
%% Формирование базы правил
a=createrule(b,a,0,axf,1);
%%%%%%%%%%%%%%%%%%%%%%%%%%
assignin(,base,,,fis,,a);%
О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-О-
addmf(a,'varType
varIndex,'mfName
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
%%%%%%%%%%%%
','mfType',mfParams)
T d "1 11 "H ~\ Q'Q'Q'Q'Q'Q'Q'Q'Q'Q'Q'Q'Q'Q'
Locdl function %%%%%%%%%%%%%%
%%%%%%%%% Формирование ф-й принадлежности %%%%%%%%%%
function d=credtemf(d,varType,vdrIndex,INndme,pin,input,top,k in,kmf,axf) kmin=min(input(:,2))*k in;kmax=max(input(:,2))*k in; b.ndme=INndme;b.range=[-k in k in]; i=1;j=1;
while i<=(length(pin)+1) if i==(length(pin)+1)
if (pin(i-1)-pin(i-2))>(kmax-pin(i-1))
par(2)=pin(i-1)+(pin(i-1)-pin(i-2))*top(j);
par(3)=2*pin(i-1)-pin(i-2)+(2*pin(i-1)-pin(i-2)-
par(2))*kmf/(1-kmf);
par(1)=pin(i-1)-kmf*(par(2)-pin(i-1))/(1-kmf);
b.mf(j).name=strcat('mf',num2str(j));
b.mf(j).type='trimf';
b.mf(j).params=par;
О
%
a=dddmf(d,vdrType,vdrIndex,strcdt('mf',num2str(j)),'trimf',par);
j=j+1;
else
par(2)=2*(kmax-pin(i-1))*top(j)+pin(i-1);
par(3)=2*(kmax-pin(i-1))+pin(i-1)+(2*(kmax-pin(i-1))+pin(i-1)-
par(2))*kmf/(1-kmf);
par(1)=pin(i-1)-kmf*(par(2)-pin(i-1))/(1-kmf);
b.mf(j).name=strcat('mf',num2str(j));
b.mf(j).type='trimf';
b.mf(j).params=par;
О
%
a=dddmf(d,vdrType,vdrIndex,strcdt('mf',num2str(j)),'trimf',par);
j=j+1;
end
else if i==1
if (pin(i+1)-pin(i))>(pin(i)-kmin)
par(2)=pin(i)-(-pin(i)+pin(i+1))*(1-top(j));
par(3)=(kmf/(1-kmf))*(pin(i)-par(2))+pin(i);
par(1)=2*pin(i)-pin(i+1)-kmf*(par(2)-
2*pin(i)+pin(i+1))/(1-kmf);
b.mf(j).name=strcat('mf,,num2str(j));
b.mf(j).type=,trimf';
b.mf(j).params=par;
%a=addmf(a,varType,varIndex,strcat('mf,,num2str(j)),,trimf,,par);
j=j+1;
else
par(2)=pin(i)-(pin(i)-kmin)*2*(1-top(j));
par(3)=(kmf/(1-kmf))*(pin(i)-par(2))+pin(i);
par(1)=pin(i)-(pin(i)-kmin)*2;
b.mf(j).name=strcat('mf',num2str(j));
b.mf(j).type='trimf';
b.mf(j).params=par;
%a=addmf(a,varType,varIndex,strcat('mf,,num2str(j)),,trimf,,par);
j=j+1;
end
else
if pin(i)<0
par(2)=pin(i)+(pin(i-1)-pin(i))*top(j);
par(3)=kmf/(1-kmf)*(pin(i)-par(2))+pin(i);
par(1)=pin(i-1)-kmf*(par(2)-pin(i-1))/(1-kmf);
b.mf(j).name=strcat('mf',num2str(j));
b.mf(j).type='trimf';
b.mf(j).params=par;
%a=addmf(a,varType,varIndex,strcat('mf,,num2str(j)),'trimf,,par);
j=j+1;
else
if pin(i-1)>0
par(2)=pin(i-1)+(pin(i)-pin(i-1))*top(j);
par(3)=(1+kmf/(1-kmf))*(pin(i)-par(2))+par(2);
par(1)=pin(i-1)-kmf*(par(2)-pin(i-1))/(1-kmf);
b.mf(j).name=strcat('mf',num2str(j));
b.mf(j).type='trimf';
b.mf(j).params=par;
%a=addmf(a,varType,varIndex,strcat('mf,,num2str(j)),'trimf,,par);
j=j+1;
else
par(3)=pin(i)*(1+kmf/(1-kmf));
par(1)=pin(i-1)*(1+kmf/(1-kmf));
par(2)=par(1)+(par(3)-par(1))*top(j);
b.mf(j).name=strcat('mf',num2str(j));
b.mf(j).type='trimf';
b.mf(j).params=par;
%a=addmf(a,varType,varIndex,strcat('mf,,num2str(j)),'trimf,,par);
j=j+1;
end
end
end
end
i=i+1;
end
if strcmp(varType,'input')
a.input(varIndex).name=b.name;
a.input(varIndex).range=b.range;
a.input(varIndex).mf=b.mf;
else
a.output(varIndex).name=b.name;
a.output(varIndex).range=b.range;
a.output(varIndex).mf=b.mf;
end
%% Графическое изображение if strcmp(varType,'input') axes(axf(varIndex+1)); plotmf(a,varType,varIndex);grid;
else
axes(axf(4));
plotmf(a,varType,varIndex);grid;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
assignin('base','fis',a);%
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
%%%%%%%%%%%%%%%%%%%%%%%%%% %%% Формирование базы правил %%%%%%%%%%%%%
function a=createrule(b,a,pres,axf,join) r=[0 0 0 1 join]; if r(5)==1
sign='\wedge'; else sign='\vee'; end d=r; nStr=1;
pin=b.pin./b.k in; pdin=b.pdin./b.k din; pout=b.pout./b.k out; for f=1:length(b.in)
for i=1:(length(pin)-1)
if b.in(f,2)<(pin(1)-pres*b.e) r(1)=1;
end
if (b.in(f,2)>(pin(i)+pres*b.e)) & (b.in(f,2)<(pin(i+1)-pres*b.e))
r(1)=i+1;
end
if b.in(f,2)>(pin(end)+pres*b.e) r(1)=length(pin)+1;
end
end
for j=1:(length(pin)-1)
if b.din(f,2)<(pdin(1)-pres*b.e) r(2)=1;
end
if (b.din(f,2)>(pdin(j)+pres*b.e)) & (b.din(f,2)<(pdin(j+1)-
pres*b.e))
r(2)=j+1;
end
if b.din(f,2)>(pdin(end)+pres*b.e) r(2)=length(pdin)+1;
end
end
for k=1:(length(pout)-1)
if b.out(f,2)<(pout(1)-pres*b.e) r(3)=1;
end
if (b.out(f,2)>(pout(k)+pres*b.e)) & (b.out(f,2)<(pout(k+1)-
pres*b.e))
r(3)=k+1;
end
if b.out(f,2)>(pout(end)+pres*b.e) r(3)=length(pout)+1;
end
end
if parity(r,d)==0
rulelist(nStr,1:5)=r;
nStr=nStr+1;
d=r;
end
end
rulelist=delidentarray(rulelist);
kol=size(rulelist);
d=struct(...
'antecedent',[],...
'consequent',[],...
'weight',[],...
'connection',[]); for i=1:kol(1)
d(i).antecedent=rulelist(i,1:2);d(i).consequent=rulelist(i,3);d(i).weight=r
ulelist(i,4);d(i).connection=rulelist(i,5);
end
a.rule=d;
assignin('base','fis',a);
o_ o. o. o. o. o_ o. o. o. nLTD a n (S0nrT nr,2DT/rn 2- 2- 2- 2- 2- 2- 2-
ooooooooo ВЫВОД ОаЗы ПраВИЛ ooooooo
ax = axes('parent',axf(end),...
'Position',[0.01 0.2 .15 0.22],...
'Color',[.7 .7 .7],...
'Box','on',...
'FontSize',8,...
'FontName','MS Sans Serif',...
'Xlim',[0 1],'Ylim',[0 1],...
'Xcolor',[0 0 0],...
'Ycolor',[0 0 0],...
'XTick',[], ...
'YTick',[]);
axf(5)=ax;axes(axf(4));axes(axf(5));
title(sprintf('\\downarrow RULE BASE \\downarrow'));
set(get(axf(5),'Title'),'FontSize',8,'FontWeight','bold');
posY=0.9;posX=0.01;
otext(0.01,posY,'Rule List=','Parent',axf(5),'FontSize',8,'FontName','MS
Sans Serif');
for i=1:length(a.rule)
if posY<0.1 posY=0.9;posX=posX+0.48;end if posX==1 break;end
if i==1 text(posX,posY,sprintf(' \\lceilod os od \\rightarrow od\\rceil',a.rule(i).antecedent(1),sign,a.rule(i).antecedent(2),a.rule(i).c onsequent),'Parent',axf(5),'FontSize',8,'FontName','MS Sans Serif');end if i==length(a.rule)
text(posX,posY,sprintf(' \\lfloor3d os od \\rightarrow od\\rfloor',a.rule(i).antecedent(1),sign,a.rule(i).antecedent(2),a.rule(i). consequent),'Parent',axf(5),'FontSize',8,'FontName','MS Sans Serif'); else
text(posX,posY,sprintf('\\mid%d %s %d \\rightarrow %d\\mid,,a.rule(i).antecedent(1),sign,a.rule(i).antecedent(2),a.rule(i).con sequent),,Parent,,axf(5),'FontSize,,8,,FontName,,,MS Sans Serif'); end
posY=posY-0.1;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Удаление одинаковых строк матрицы%%%%%%%%% function c=delidentarray(d) s=size(d); for i=1:(s(1)-1) d=t(d,i);
end
c=d;
function b=t(a,i) s=size(a); if i>=s(1) b=a; return
end
c=a(i,1:end);b=a(1:i,1:end); for j=(i+1):s(1) p=a(j,1:end); if parity(c,p)~=1
b(end+1,1:end)=a(j,1:end);
end
end
%% Сравнение двух матриц (1 - если равны 0 - в противном случае)%%%%% function z=parity(x,y) n=eq(x,y); for i=1:length(n) if n(i)~=1 z=0; return
end
end
z=1;
Построение поверхности отклика function dosurf(a,axf) axes(axf(1)); gensurf(a); rotate3d on
set(axf(1),,TickDir,,,out,,,CameraPosition,,[-5 200
1],,CameraPositionMode,,,manual,);
title(,Поверхность отклика,);
set(get(axf(1),,title,),,FontName,,,MS Sans Ser- if,,,FontSize,,10,,FontWeight,,,bold,);
Построение переходного процесса
function graf(a,b,fg,fig)
Y=,out, out\prime,;
out=evalfis([(b.in(:,2)*b.k in),(b.din(:,2)*b.k din)],a); axes(fg(1));
axis([0 b.out(end,1) min(b.out(:,2)) max(b.out(:,2))]); plot(b.out(:,1),(b.out(:,2)*b.k out),,LineWidth,,2); hold on
mistake=0;
for i=1:(length(b.out)-1)
mistake=mistake+((b.out(i,2)*b.k out-out(i))A2)*(b.out(i+1,1)- b.out(i,1))/b.out(end,1); end
set(fg(6),'color',[0.7 0.7 0.7]); uicontrol('style','text',...
'string',sprintf('3E',mistake),...
'units','norm',...
'Background',[0.7 0.7 0.7],...
'position',[0.082 0.065 .12 .03],...
'FontSize',9,'FontName','MS Sans Serif','FontWeight','bold');
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
oooooooooooooo
LineWidth',2);grid;
plot(b.in(:,1),out(:),'-r',' title('Переходный
процесс'); xlabel('t, c');ylabel(Y);
set(get(fg(1),'title'),'FontName','MS Sans Ser-
if','FontSize',10,'FontWeight','bold');
set(get(fg(1),'XLabel'),'FontName','MS Sans Serif'
legend('out','out'',1); hold off
FontSize
6);
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
oooooooooooo
evaluate mistake
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
oooooooooooooooooooo
function a=style2style(a,varType,varIndex,styleMF,NumMF,axf) if styleMF==1
styleMF='trimf'; elseif styleMF==2
styleMF='gaussmf'; elseif styleMF==3
styleMF='gauss2mf'; elseif styleMF==4
styleMF='dsigmf'; elseif styleMF==5
styleMF='gbellmf'; elseif styleMF==6
styleMF='pimf'; elseif styleMF==7
styleMF='psigmf'; elseif styleMF==8 styleMF='smf'; elseif styleMF==9
styleMF='sigmf'; elseif styleMF==10 styleMF='zmf'; elseif styleMF==11
styleMF='trapmf';
end
if strcmp(varType,'input')
if NumMF==(length(a.input(varIndex).mf)+1) for i=1:length(a.input(varIndex).mf) a.input(varIndex).mf(i).params =
mf2mf(a.input(varIndex).mf(i).params,a.input(varIndex).mf(i).type,styleMF);
a.input(varIndex).mf(i).type=styleMF;
end
else a.input(varIndex).mf(NumMF).params = mf2mf(a.input(varIndex).mf(NumMF).params,a.input(varIndex).mf(NumMF).type,s tyleMF);
a.input(varIndex).mf(NumMF).type=styleMF;
end
if NumMF==(length(a.output(varIndex).mf)+1) for i=1:length(a.output(varIndex).mf) a.output(varIndex).mf(i).params =
mf2mf(a.output(varIndex).mf(i).params,a.output(varIndex).mf(i).type,styleMF
);
a.output(varIndex).mf(i).type=styleMF;
end
else
a.output(varIndex).mf(NumMF).params =
mf2mf(a.output(varIndex).mf(NumMF).params,a.output(varIndex).mf(NumMF).type
,styleMF);
a.output(varIndex).mf(NumMF).type=styleMF;
end
end
%% Обновление графиков %%% if strcmp(varType,'input') axes(axf(varIndex+1)); plotmf(a,varType,varIndex);grid;
else
axes(axf(4));
plotmf(a,varType,varIndex);grid;
end
%%%%%%%%%%%%%%%%%%%%%%%%%% assignin('base','fis',a);%
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
%%%%%%%%%%%%%%%%%%%%%%%%%%
Смена метода
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
%%%%%%%%%%%%%%%%%%%%%%%%%%% function changeAndMethod(Num,a) if Num==1
Method='min'; elseif Num==2
Method='prod'; elseif Num==3
Method='myfun';
end
a.andMethod=Method;
assignin('base','fis',a);
function changeOrMethod(Num,a) if Num==1
Method='max'; elseif Num==2
Method='probor';
end
a.orMethod=Method;
assignin('base','fis',a);
function changeDefuzMethod(Num,a) if Num==1
Method='centroid'; elseif Num==2
Method='bisector'; elseif Num==3
Method='mom'; elseif Num==4
Method='lom'; elseif Num==5
Method='som';
end
a.defuzzMethod=Method;
assignin('base,,,fis,,a);
CRFUZ
Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-Q-
оооооооооооо
ооооооооооооо END OF CODE
Научное издание
Вячеслав Алексеевич СОЛОВЬЕВ Сергей Петрович ЧЕРНЫЙ
ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ В ЗАДАЧАХ УПРАВЛЕНИЯ. ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ
Монография
Подписано в печать
Формат 60х90/16. Печать офсетная Бумага офсетная. Усл. п. л. 17,25. Уч.-изд. л.
Тираж 150 экз. Заказ
Издательство «Дальнаука» 690041, Владивосток, ул. Радио, 7.
Отпечатано в полиграфической лаборатории Г осударственного образовательного учреждения высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет» 681013, Комсомольск-на-Амуре, пр. Ленина, 27.
2. Первый максимум (First-of-Maxima). Чёткая величина переменной вывода находится как наименьшее значение, при котором достигается максимум итогового нечёткого множества, т. е. (рис. 2.12, а)
z0 = min (z | C (z) = max
1 х е с и х е В; С, В - чёткие множества. Пусть тс(х) = 1, тв(х) = 1.
Т огда тспВ (х) = тт{тс (х); тВ (х)} = тт{1;1} = 1, что означает х е с п В .
2010