Глава 5. Синтез многокаскадных нечётких систем управления технологическими процессами

На сегодняшний день системы, построенные на принципах нечёткой логики, находят своё применение во многих сферах человеческой деятель­ности и области их использования постоянно расширяются. Такие системы используются при управлении сложными технологическими процессами, при управлении бизнес-процессами, в системах поддержки принятия ре­шений, при создании различных приборов и бытовой техники.

Одним из направлений развития нечётких систем управления являет­ся построение нечётких экспертных систем основанных на принципах многокаскадности. Использование таких структурных решений позволяет существенно повысить интеллектуальность системы, что впоследствии позволит расширить диапазон применения нечётких систем. Первый кас­кад нечёткого регулятора можно рассматривать как экспертную систему, которая на основе имеющихся входных данных производит управление ре­гуляторами, находящимися во втором каскаде.

5.1. Многокаскадные нечётких регуляторы систем управления пиролизными установками мобильного

типа.

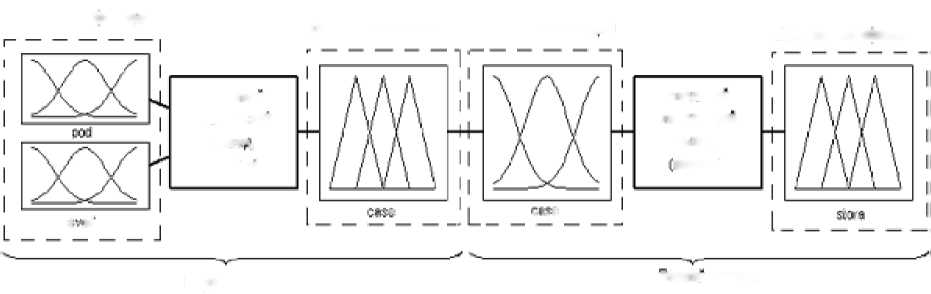
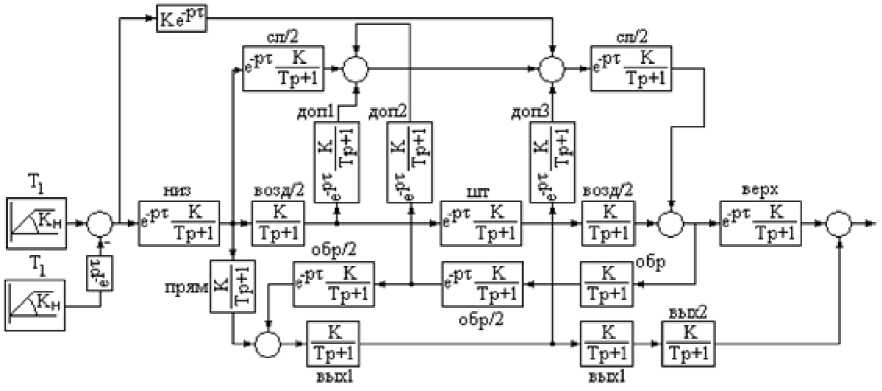
Построим многокаскадный нечёткий регулятор пиролизной установ­ки мобильного типа с пассивным способом управления (рис. 5.1), состоя­щий из двух каскадов (рис. 5.2).

Рис. 5.1 Структурная схема пиролизной установки с пассивным способом

регулирования

Блок фаззиоикации

Бл ок дефзгэйфикации Блок фаээифмсации

Блок д&фаззификацни

Нечеткии

логическим

шеи-.

(гваїгівл)

■ ■■

. :.V

Нз'-рткии

Г0ГИНЄШ1И

БЬ БОД

mamcfeni)

' : ■

Первый НЛР имеет два входа, соответствующие температуре пода и свода установки (pod и svod), и один выход (case). На выходе регулятора формируется сигнал, соответствующий тому или иному сочетанию значе­ний pod и svod. Второй НЛР имеет один вход и один выход. Он осуществ­ляет регулирование пространственным положением шторы.

старая каскад

Перэый каскад

Рис. 5.2. Многокаскадный нечёткий регулятор

Функции принадлежности для входной лингвистической переменной pod первого каскада представлены на рис. 5.3.

Рис. 5.3. Функции принадлежности лингвистической переменной pod Обозначениям, приведённым на рис. 5.3, соответствуют следующие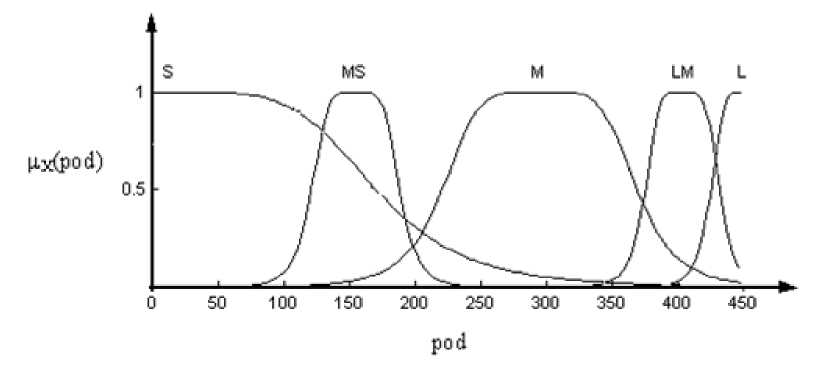

лингвистические значения:

£ - «малое близкое к нулю»;

МБ - «малое близкое к среднему»;

М - «среднее»;

ЬМ - «большое близкое к среднему»;

Ь - «большое».

Функции принадлежности для входной лингвистической переменной зуой первого каскада представлены на рис. 5.4.

Рис. 5.4. Функции принадлежности лингвистической переменной svod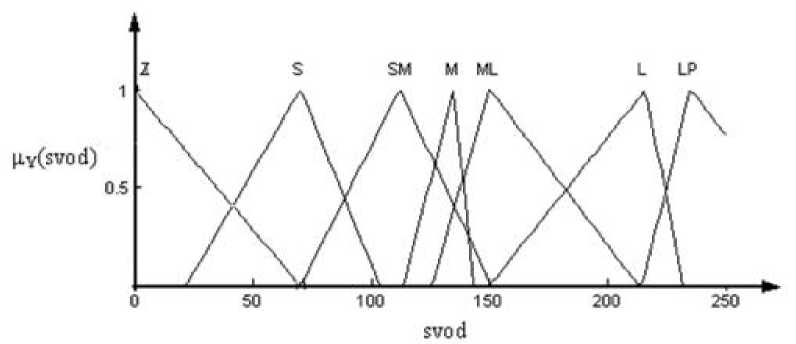

Обозначениям, приведённым на рис. 5.4, соответствуют следующие лингвистические значения:

Z - «нулевое»;

S - «малое близкое к нулю»;

SM - «малое близкое к среднему»;

М - «среднее»;

LM - «большое близкое к среднему»;

L - «большое»;

LB - «очень большое».

Функции принадлежности для выходной лингвистической перемен­ной case первого каскада представлены на рис. 5.5.

Рис. 5.5. Функции принадлежности лингвистической переменной case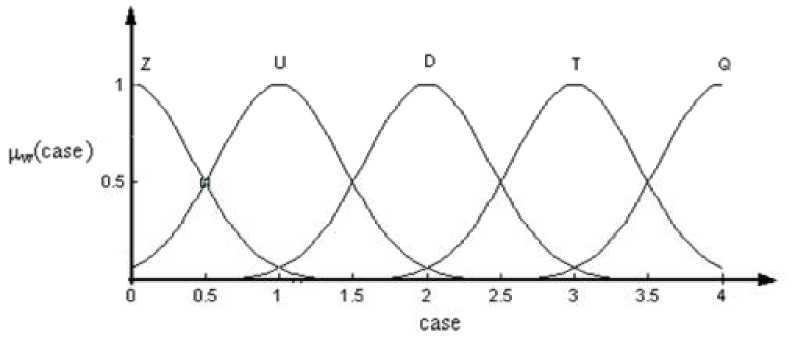

Обозначениям, приведённым на рис. 5.5, соответствуют следующие лингвистические значения:

Z - «нулевой»;

U - «первый»;

D - «второй»;

T - «третий»;

Q - «четвертый».

Дефаззификация происходит на основе стандартного метода центра тяжести.

БЗ будет состоять из 11 продукционных правил вместо 35 возмож­ных, рассчитанных из условия её полноты.

Если pod есть S и svod есть Z, то case есть Z;

Если pod есть S и svod есть S, то case есть Z;

Если pod есть S и svod есть SM, то case есть D;

Если pod есть L и svod есть M, то case есть T;

Если pod есть L и svod есть ML, то case есть T;

Если pod есть L и svod есть L, то case есть T;

Если pod есть L и svod есть LP, то case есть Q;

Если pod есть S и svod есть M, то case есть T;

Если pod есть L и svod есть SM, то case есть D;

Если pod есть L и svod есть S, то case есть U;

Если pod есть MS и svod есть SM, то case есть T.

Для второго каскада функции принадлежности для входной лингви­стической переменной case представлены на рис. 5.6.

Рис. 5.6. Функции принадлежности лингвистической переменной case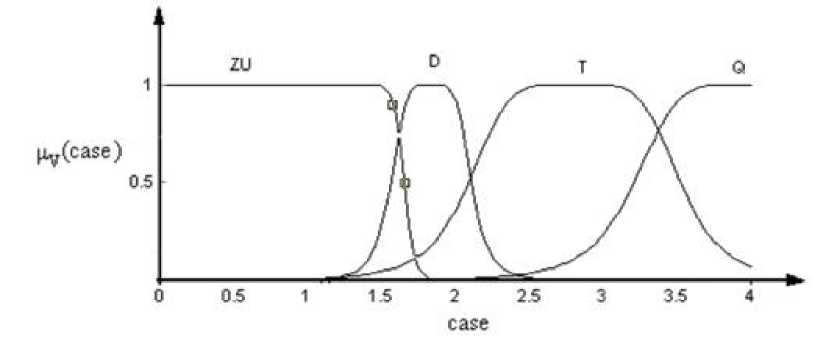

Обозначениям, приведённым на рис. 5.6, соответствуют следующие лингвистические значения:

ZU - «нулевой и первый»;

D - «второй»;

T - «третий»;

Q - «четвёртый».

Функции принадлежности для выходной лингвистической перемен­ной stora второго каскада представлены на рис. 5.7.

Рис. 5.7. Функции принадлежности лингвистической переменной stora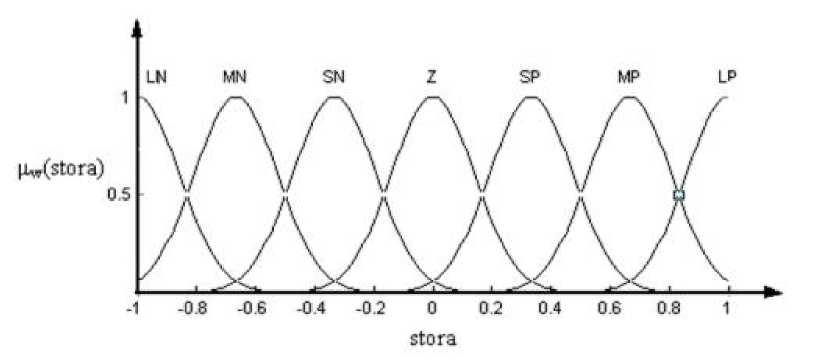

Лингвистическая переменная stora принимает следующие лингви­стические значения:

LN - «отрицательное большое»;

MN - «отрицательное среднее»;

SN - «отрицательное малое»;

Z - «нулевое»;

SP - «положительное малое»;

MP - «положительное среднее»;

LP - «положительное большое».

Дефаззификация происходит на основе метода среднего максимума. БЗ будет состоять из 4 продукционных правил.

Если case есть ZU, то stora есть LP;

Если case есть D, то stora есть SP;

Если case есть T, то stora есть SN;

Если case есть Q, то stora есть MN.

Смоделируем процесс пиролиза древесины в углевыжигательной пе­чи с синтезированным НЛР. Полученные динамические характеристики сравним с характеристиками системы без регулятора (рис. 5.8).

1_Р Ч *

Рис. 5.8 - Динамические характеристики системы управления: 1 - классическая система, 2 - система с НЛР.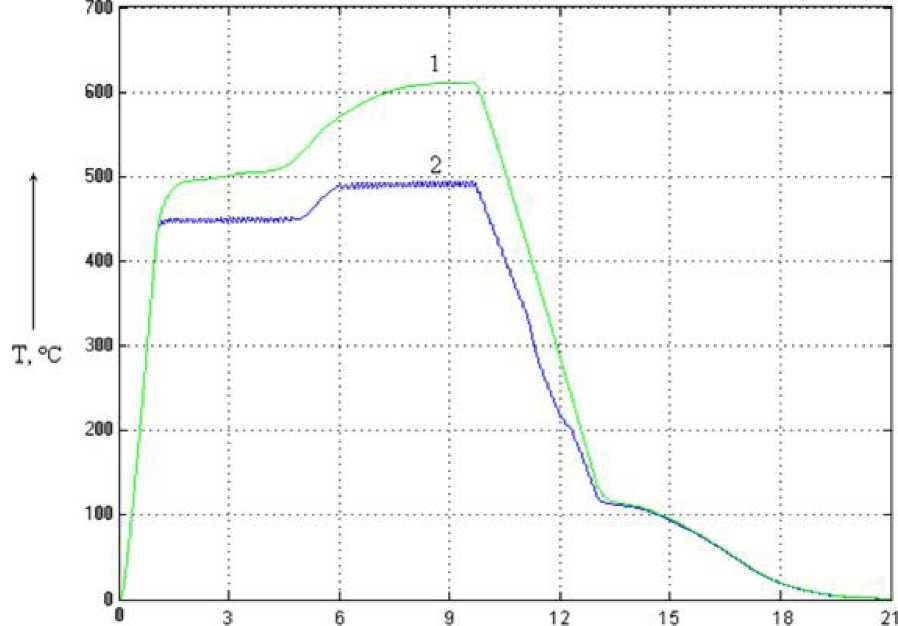

Анализ результатов моделирования показывает, что введение нечёт­кого управления несколько повышает стабилизацию температурного поля, уменьшая температурное рассогласование углевыжигательной печи на этапе прокаливания угля (величина рассогласования не превышает 60 °С). Температура удерживается в диапазоне 450...550 ^оС, т.е. в данном случае применение многокаскадного НЛР обеспечивает улучшение качества ре­гулирования.

1. Синтез многокаскадного нечёткого регулятора с алгоритмом вывода Сугено/Мамдани

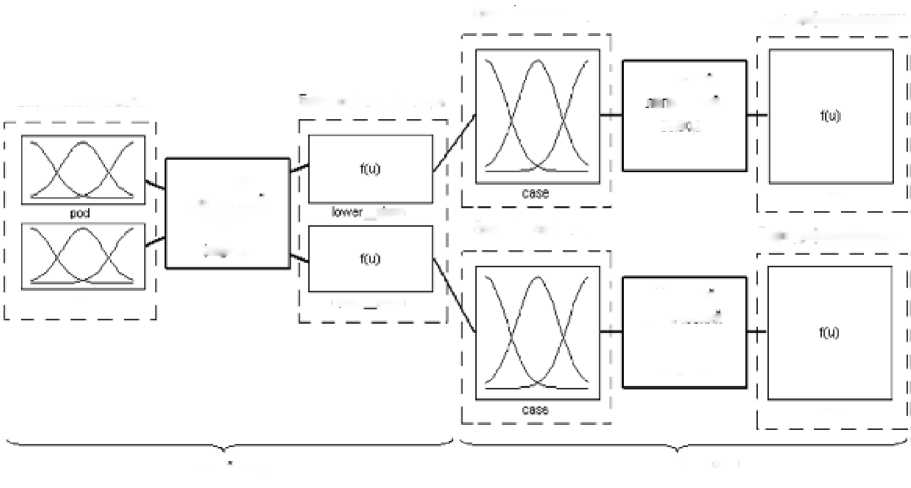
Построим двухкаскадный НЛР с раздельным управление нижней и верхней шторами (рис. 5.9). Первый НЛР имеет два входа, соответствую­щие температуре пода и свода установки (pod и svod), и два выхода. На выходах регулятора формируются сигналы, соответствующий тому или иному сочетанию значений pod и svod, индивидуальные для нижней и верхней штор. Второй каскад состоит из двух одинаково настроенных ре­гуляторов, управляющих пространственным положением нижней и верх­ней штор (lower stora и upper stora). Каждый такой НЛР имеет один вход и один выход.

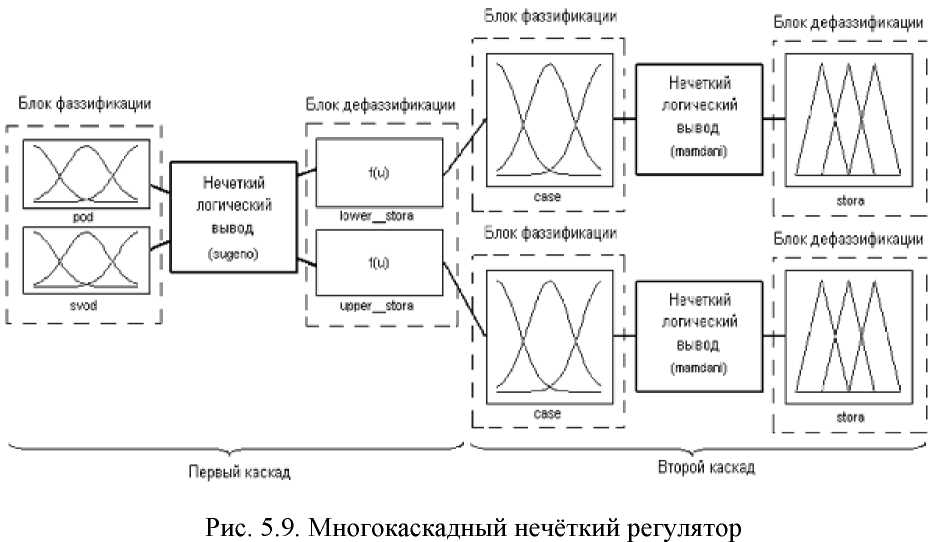
Построим первый каскад с использованием алгоритма вывода Суге- но. Вид функций распределения входных лингвистических переменных pod и svod первого каскада будет идентичен функциям, приведённым на рис. 5.3 и 5.4. Функции принадлежности выходных переменных - констан­ты, т.е. НЛР с алгоритмом вывода Сугено имеет нулевой порядок.

Дефаззификация происходит на основе стандартного метода центра тяжести.

БЗ будет состоять из 11 продукционных правил вместо 35 возмож­ных, рассчитанных из условия её полноты.

Если pod есть Если pod есть Если pod есть Если pod есть Если pod есть Если pod есть Если pod есть Если pod есть Если pod есть Если pod есть Если pod есть

£ и есть 2, то \ower_stora есть 0 и upper_stora есть 0;

£ и 8Уой есть £, то \ower_stora есть 0 и ыррвг_81ога есть 0;

£ и 8Уой есть £М, то \ower_stora есть 2 и иррег_8^га есть 2; ЬМ и svod есть М, то \ower_stora есть 3 и upper_stora есть 3; ЬМ и svod есть ЬМ, то \ower_stora есть 3 и upper_stora есть 3; ЬМ и svod есть Ь, то \ower_stora есть 3 и upper_stora есть 3; ЬМ и svod есть ЬВ, то \ower_stora есть 4 и upper_stora есть 4; £ и svod есть М, то \ower_stora есть 3 и upper_stora есть 3; ЬМ и svod есть £М, то \ower_stora есть 3 и upper_stora есть 2; ЬМ и svod есть £, то \ower_stora есть 2 и upper_stora есть 1;

Ь и svod есть £М, то \ower_stora есть 3 и upper_stora есть 3.

Рис. 5.10. Функции принадлежности лингвистической переменной case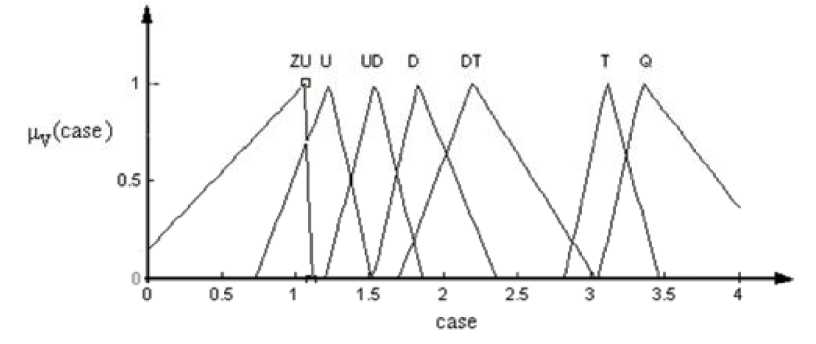

Для второго каскада функции принадлежности для входной лингви­стической переменной case представлены на рис. 5.10.

Обозначениям, приведённым на рис. 5.10, соответствуют следующие лингвистические значения:

2. - «нулевой»; и - «первый»;

иО - «между первым и вторым»;

О - «второй»;

ОТ - «второй, близкий к третьему»;

Т- «третий»;

Q - «четвертый».

Функции принадлежности для выходной лингвистической перемен­ной $1ота второго каскада представлены на рис. 5.11.

Рис. 5.11. Функции принадлежности лингвистической переменной 51ота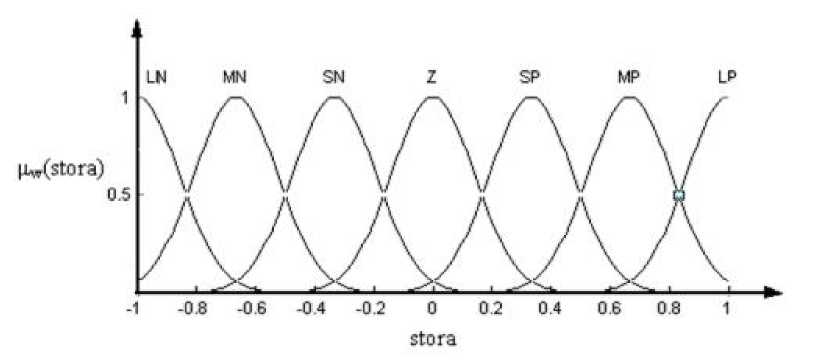

Лингвистическая переменная 81ота принимает следующие лингви­стические значения:

ЬИ - «отрицательное большое»;

МИ - «отрицательное среднее»;

РИ - «отрицательное малое»;

2 - «нулевое»;

РР - «положительное малое»;

МР - «положительное среднее»;

ЬР - «положительное большое».

Дефаззификация происходит на основе стандартного метода центра тяжести.

БЗ будет состоять из 7 продукционных правил.

Если case есть Z , то stora есть LP;

Если case есть U, то stora есть LP;

Если case есть UD, то stora есть Z;

Если case есть D, то stora есть SN;

Если case есть DT, то stora есть SN;

Если case есть T, то stora есть SN;

Если case есть Q, то stora есть SN.

Смоделируем процесс пиролиза древесины в углевыжигательной пе­чи с синтезированным НЛР. Полученные динамические характеристики сравним с характеристиками системы без регулятора (рис. 5.12).

Рис. 5.12. Динамические характеристики процесса пиролиза. 1 - система

без НЛР; 2 - система с многокаскадным НЛР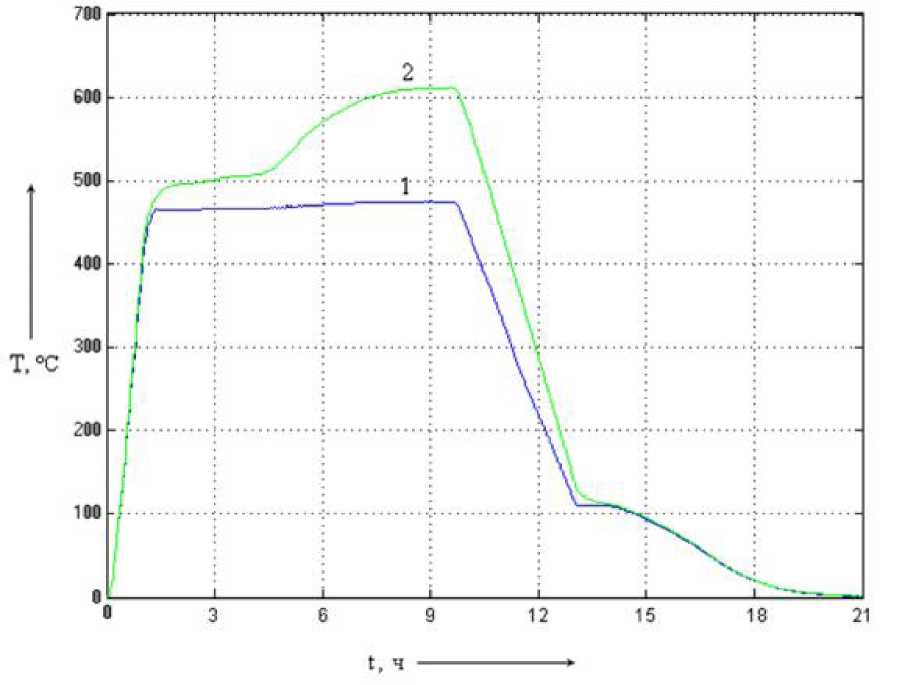

Анализ результатов моделирования показывает, что введение нечёт­кого управления повышает стабилизацию температурного поля, уменьшая температурное рассогласование углевыжигательной печи на этапе прока­ливания угля. Температура удерживается в диапазоне 460...470 ^оС, т.е. в данном случае применение многокаскадного НЛР с раздельным управле­нием верхней и нижней шторами обеспечивает улучшение качества регу­лирования.

2. Синтез многокаскадного нечёткого регулятора с алгоритмом вывода Сугено/Сугено

Елок (ратификации

Блёк деоайИфнкйцни

Начеткии

О ИЧ0Ш1И

Блок фзззификацин

ьлокдафаззифнкацни

svod

Нечеткий

логическим

ВЫВОД

І5ЦЖПО)

ттсг-а

шдоґ stars

Елок фюэнфикации

ИНН 1,4,

(sugenoj

Нечетки И

логическим

вывод

СНДОО)

SlQfi

Елок д ооооэиф ІЖС ЦП 1%

Построим НЛР, аналогичный предыдущему, однако во втором кас­каде будем использовать алгоритмом вывода Сугено (рис. 5.13).

■

Второй каскад

tiers

Первый каскад

Рис. 5.13. Многокаскадный нечёткий регулятор

Для второго каскада функции принадлежности для входной лингви­стической переменной case представлены на рис. 5.14.

Рис. 5.14. Функции принадлежности лингвистической переменной case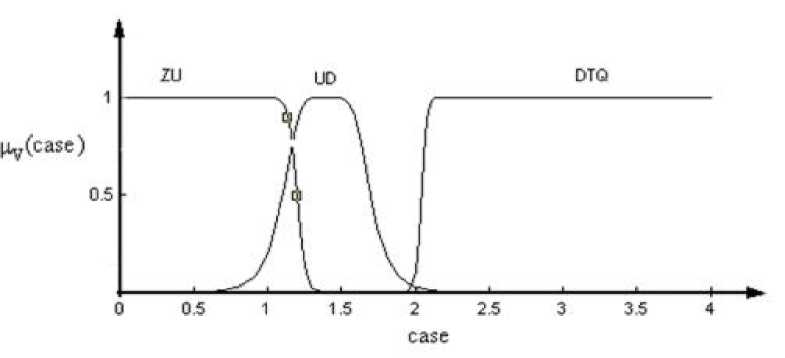

Обозначениям, приведённым на рис. 5.14, соответствуют следующие лингвистические значения:

ZU - «нулевой и первый»;

UD - «между первым и вторым»;

DTQ - «второй, третий, четвертый».

Функции принадлежности выходных переменных - константы.

БЗ будет состоять из 3 продукционных правил.

Если case есть ZU, то stora есть 1;

Если case есть UD, то stora есть 0;

Если case есть DTQ, то stora есть -1.

Смоделируем процесс пиролиза древесины в углевыжигательной пе­чи с синтезированным НЛР. Полученные динамические характеристики сравним с характеристиками системы без регулятора (рис. 5.15).

Рис. 5.15. Динамические характеристики процесса пиролиза (1 - система без НЛР; 2 - система с многокаскадным НЛР)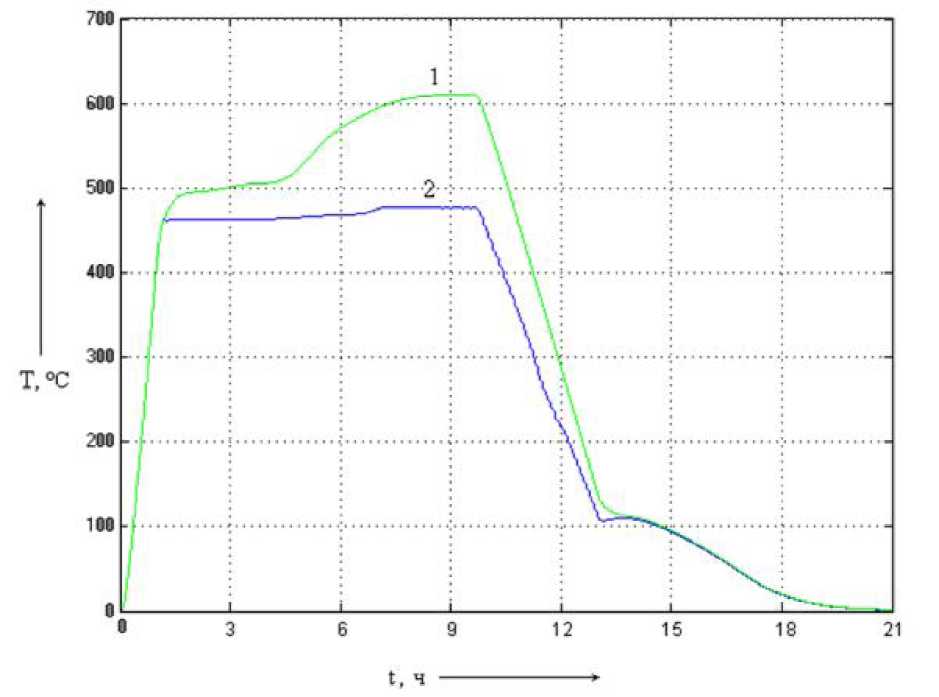

Анализ результатов моделирования показывает, что введение нечёт­кого управления повышает стабилизацию температурного поля, уменьшая температурное рассогласование углевыжигательной печи на этапе прока­ливания угля. Температура удерживается в диапазоне 460...480 ^оС, т.е. в данном случае применение многокаскадного НЛР с раздельным управле­нием верхней и нижней шторами обеспечивает улучшение качества регу­лирования.

3. Анализ систем управления построенных с различными сочетаниями алгоритмов нечёткого вывода

Смоделируем процесс пиролиза древесины в углевыжигательной пе­чи с синтезированными НЛР. Полученные динамические характеристики сравним с характеристиками системы без регулятора (рис. 5.16).

Рис. 5.16. Динамические характеристики процесса пиролиза (1 - система без НЛР; 2 - система с однокаскадным НЛР; 3 - система с многокаскадным НЛР с алгоритмом вывода Мамдани/Мамдани; 4 - система с многокаскадным НЛР с алгоритмом вывода Сугено/Мамдани с раздельным управлением шторами; 5 - система с многокаскадным НЛР с алгоритмом вывода Сугено/Сугено с раздельным управлением шторами)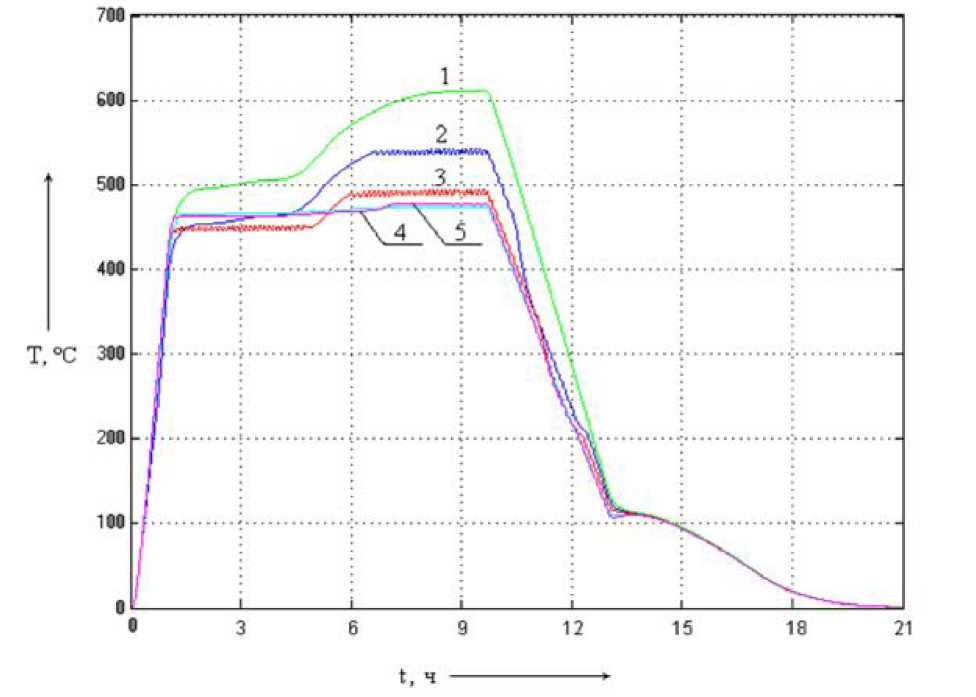

В ходе процесса пиролиза температура в системе без НЛР на этапе прокаливания угля выходит за пределы желаемой области. Анализируя по­лученные характеристики, можно сказать, что система управления с лю-

бым из четырёх НЛР позволяет улучшить процесс пиролиза за счёт вырав­нивания температур во всем объёме среды сугливания, но наиболее эффек­тивным является НЛР с раздельным управлением верхней и нижней што­рами. Разница температур между подом и сводом камеры при использова­нии этих регуляторов на этапе прокаливания угля составляет всего не бо­лее 5 °С, в то время как при использовании других регуляторов она состав­ляет порядка 50°С. Такие результаты получаются за счёт более гибкого управления при использовании НЛР с раздельным управлением шторами.

Как следует из результатов моделирования, применение НЛР с ис­пользованием любого из алгоритмов вывода позволяет повысить качество получаемого в процессе пиролиза древесного угля за счёт уменьшения температурного рассогласования на этапах экзотермической реакции и прокаливания угля.

Применение многокаскадных нечётких регуляторов позволяет более точно стабилизировать температуру на этапе прокаливания угля и удержи­вать её в требуемом диапазоне 450...550 ^оС. НЛР с алгоритмом вывода по Сугено позволяет добиться более равномерного распределения температур внутри камеры установки при существенном сокращении базы правил ре­гулятора.

Рассмотрим поведение системы при действии возмущений различно­го характера. Исследуем поведение системы при различных изменениях её параметров, связанных с изменением температурного режима работы. Для этого будем менять соотношения параметров процесса пиролиза, не изме­няя при этом настройки НЛР.

Рассмотрим влияние изменения параметров самой системы путём изменения коэффициента усиления первого апериодического звена К і на -10...+10%. На рис. 5.17 приведены переходные процессы системы без ре­гулятора.

Рис. 5.17. Динамические характеристики системы без регулятора (1 - при

коэффициенте усиления 110 % К_/; 2 - при коэффициенте усиления 105 % К_/; 3 - при коэффициенте усиления 100 % К_/; 4 - при коэффициенте усиления 95 % К_/;

5 - при коэффициенте усиления 90 % К_/)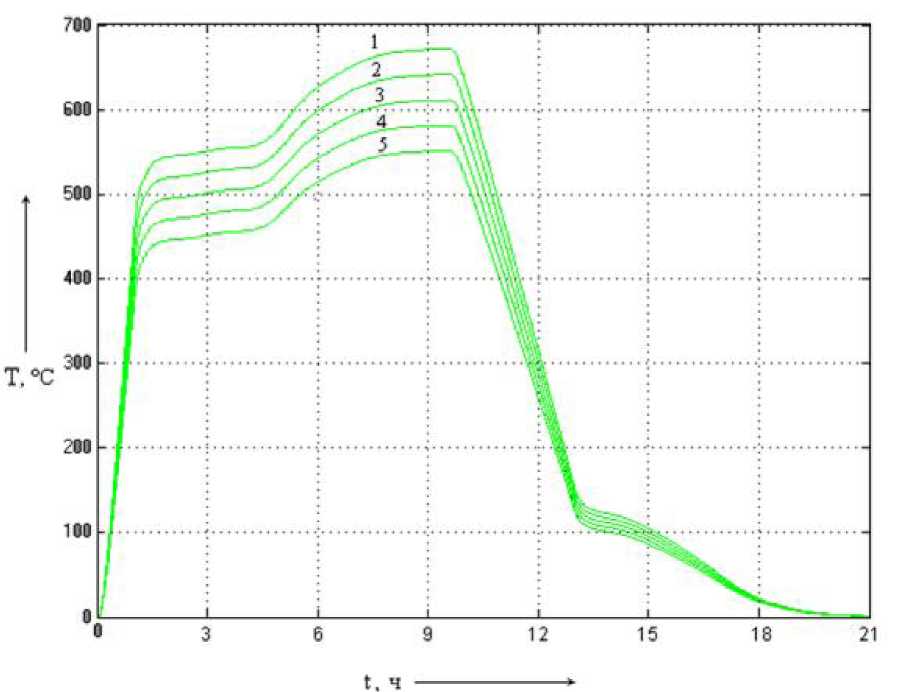

При увеличении параметра К_/ первого апериодического звена темпе­ратура прокаливания угля в системе без регулятора намного превышает желаемый диапазон 450...550 ^оС. Температурное рассогласование превы­шает 100 °С. С уменьшением К температура приближается к желаемому диапазону, однако рассогласование сохраняется большим.

Рис. 5.18. Динамические характеристики системы с однокаскадным нечётким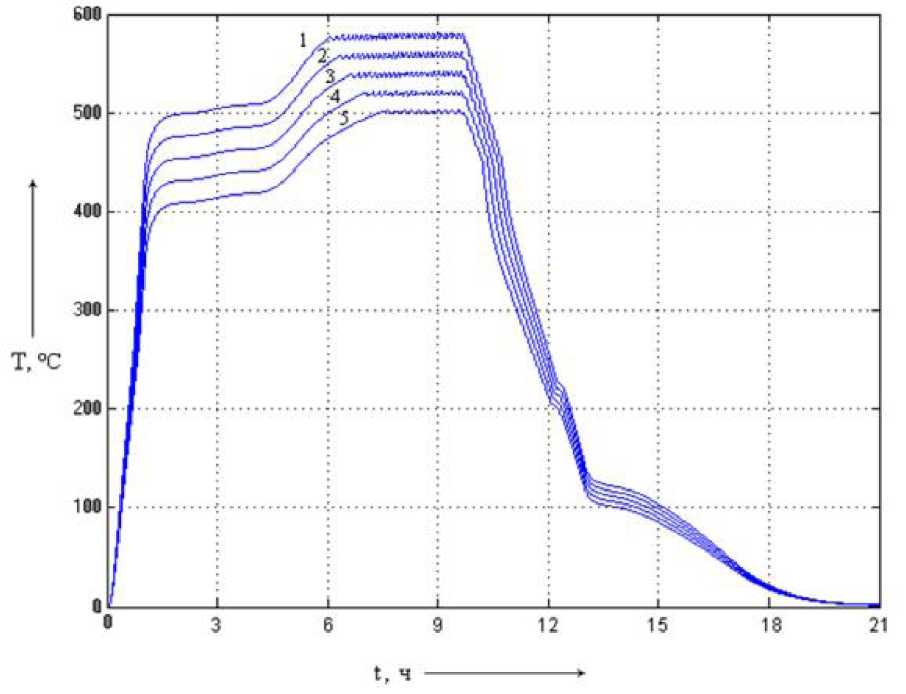

регулятором (1 - при коэффициенте усиления 110 % R_f; 2 - при коэффициенте усиления 105 % Rf, 3 - при коэффициенте усиления 100 % Rf, 4 - при коэффициенте усиления 95 % Rf, 5 - при коэффициенте усиления 90 % R_f)

Анализ результатов моделирования (рис. 5.18) показывает, что вве­дение нечёткого управления несколько повышает стабилизацию темпера­турного поля. При изменении R_f температура изменяется в несколько бо­лее широком диапазоне, чем желаемый, однако это превышение незначи­тельно, т.е. в данном случае применение однокаскадного НЛР обеспечива­ет уменьшение чувствительности к изменению параметров системы.

Рис. 5.19. Динамические характеристики системы с многокаскадным нечётким регулятором (1 - при коэффициенте усиления 110 % К^; 2 - при коэффициенте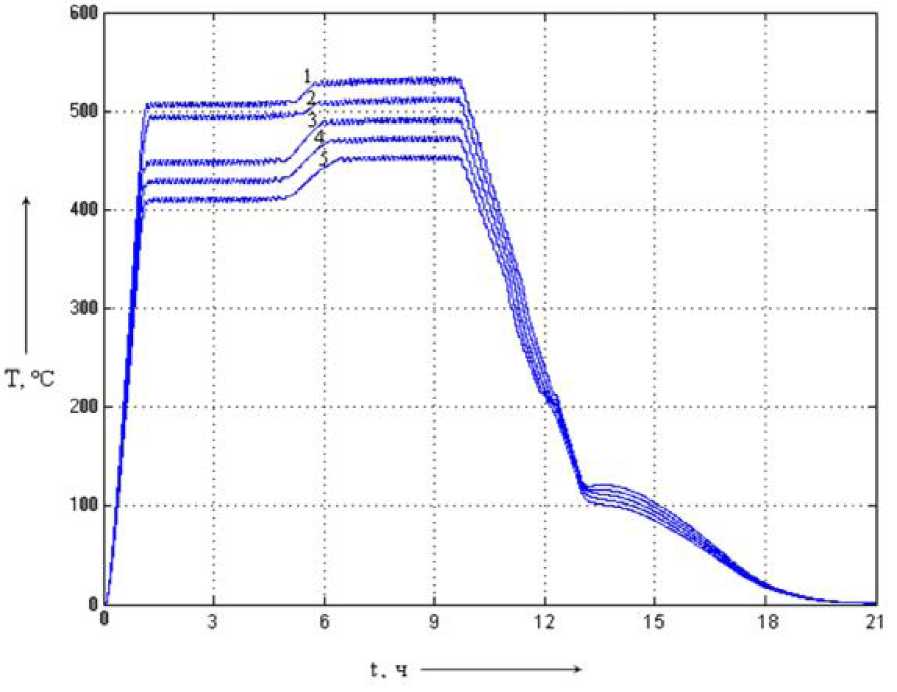

усиления 105 % К_]; 3 - при коэффициенте усиления 100 % К_]; 4 - при коэффициенте усиления 95 % К у, 5 - при коэффициенте усиления 90 % К_])

Анализ результатов моделирования показывает, что введение нечёт­кого управления несколько повышает стабилизацию температурного по- ля(рис. 5.19). При увеличении параметра К] графики переходных процес­сов располагаются плотнее, что позволяет удерживать температура на эта­пе прокаливания угля в желаемом диапазоне и уменьшить температурное рассогласование. С уменьшением К_] температура становится незначитель­но ниже желаемого диапазона, а температурное рассогласование сохраня­ется небольшим - до 50 ^оС, т.е. в данном случае применение многокаскад­ного НЛР обеспечивает уменьшение чувствительности к изменению пара­метров системы.

Рис. 5.20. Динамические характеристики системы с многокаскадным нечётким

регулятором с раздельным управлением шторами с алгоритмом вывода Сугено/Мамдани (1 - при коэффициенте усиления 110 % К_]; 2 - при коэффициенте усиления 105 % К_]; 3 - при коэффициенте усиления 100 % К_]; 4 - при коэффициенте усиления 95 % К_]; 5 - при коэффициенте усиления 90 % К_])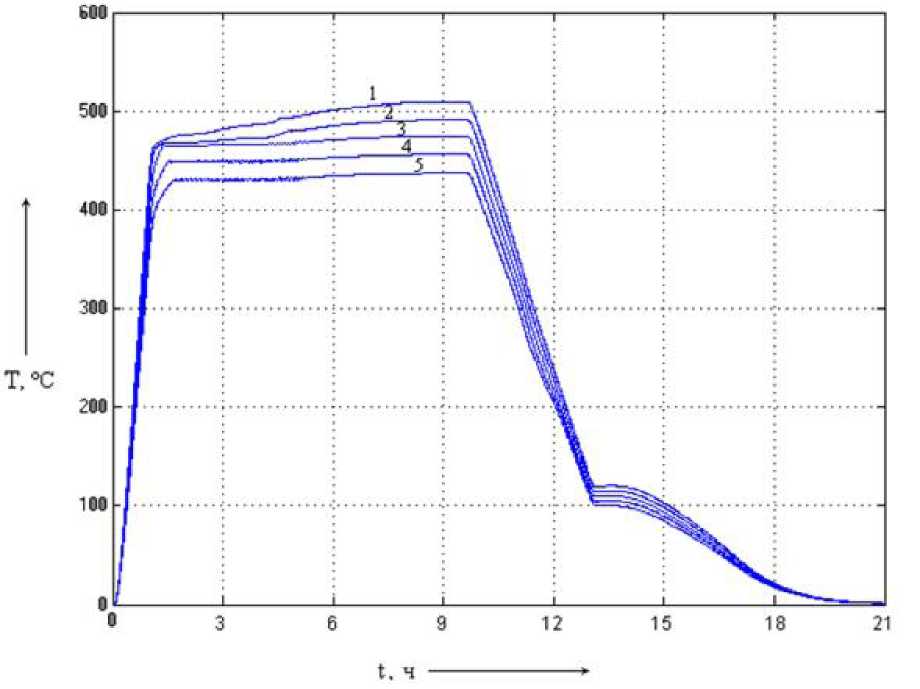

Анализ результатов моделирования показывает, что введение нечёт­кого управления повышает стабилизацию температурного поля, уменьшая температурное рассогласование углевыжигательной печи на этапе прока­ливания угля. При изменении К_] температура удерживается в диапазоне 420...510 ^оС, что приближено с желаемому диапазону, т.е. в данном случае применение многокаскадного НЛР с раздельным управлением верхней и нижней шторами обеспечивает уменьшение чувствительности к измене­нию параметров системы и улучшение качества регулирования (рис. 5.20).

Рис. 5.21. Динамические характеристики системы с многокаскадным нечётким регулятором с раздельным управлением шторами с алгоритмом вывода Сугено/Сугено (1 - при коэффициенте усиления 110 % К_]; 2 - при коэффициенте усиления 105 % К у, 3 - при коэффициенте усиления 100 % К у, 4 - при коэффициенте усиления 95 % К у, 5 - при коэффициенте усиления 90 % К_])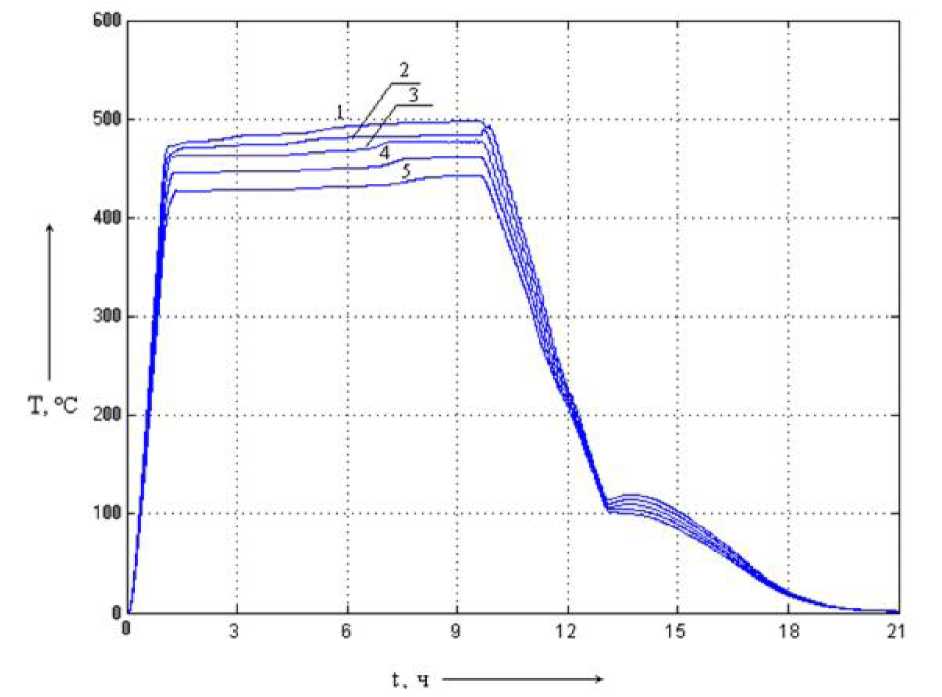

Анализ результатов моделирования показывает, что введение нечёт­кого управления повышает стабилизацию температурного поля, уменьшая температурное рассогласование углевыжигательной печи на этапе прока­ливания угля (рис. 5.21). При изменении К_] графики расположены плотно, температура удерживается в диапазоне 420...500 ^оС, что приближено с же­лаемому диапазону, т.е. в данном случае применение многокаскадного НЛР с раздельным управлением верхней и нижней шторами обеспечивает уменьшение чувствительности к изменению параметров системы и улуч­шение качества регулирования.

Для оценки влияния коэффициента усиления первого апериодиче­ского звена на переходный процесс построим сводную характеристику для температуры в точке начала экзотермической реакции (4-5 ч) в зависимо­

9 К

9Ж]

06 К

Рис. 5.22. Зависимость температуры начала экзотермической реакции от К_і (1 - система без НЛР; 2 - система с однокаскадным НЛР; 3 - система с многокаскадным НЛР с алгоритмом вывода Мамдани/Мамдани; 4 - система с многокаскадным НЛР с алгоритмом вывода Сугено/Мамдани с раздельным управлением шторами; 5 - система с многокаскадным НЛР с алгоритмом вывода Сугено/Сугено с раздельным управлением шторами)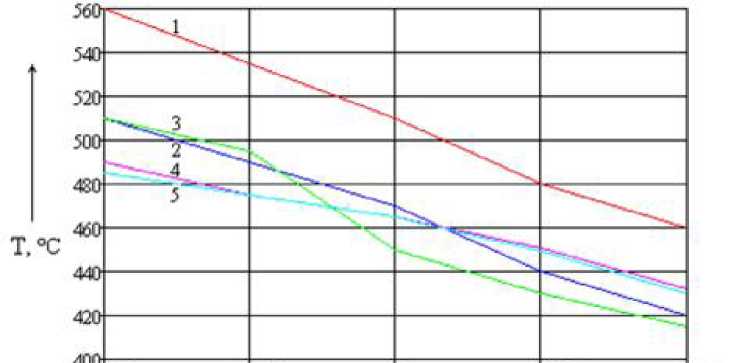

сти от К_j (рис. 5.22).

Система управления с любым из четырех НЛР позволяет уменьшить чувствительность к изменению параметра К\ первого апериодического звена системы и улучшить процесс пиролиза. При изменении К темпера­тура удерживается в диапазоне 450...550 °С или близко к нему. Система же без НЛР выходит из допустимых температурных пределов, в результате чего полученный древесный уголь окажется низкого качества. Точка нача­ла экзотермической реакции смещается в больших пределах - до 100 °С.

Наиболее эффективным является НЛР с раздельным управлением верхней и нижней шторами. Графики переходных процессов расположены близко друг к другу и не выходят за пределы желаемого диапазона. Точка

начала экзотермической реакции смещается в пределах не более 60 °С. Та­кие результаты получаются за счет более гибкого управления при исполь­зовании НЛР с раздельным управлением шторами.

Рассмотрим влияние изменения параметров самой системы путем изменения постоянной времени первого апериодического звена Т/.

На рис. 5.23 приведены переходные процессы системы без регулято­ра.

Рис. 5.23. Динамические характеристики системы без регулятора (1 - при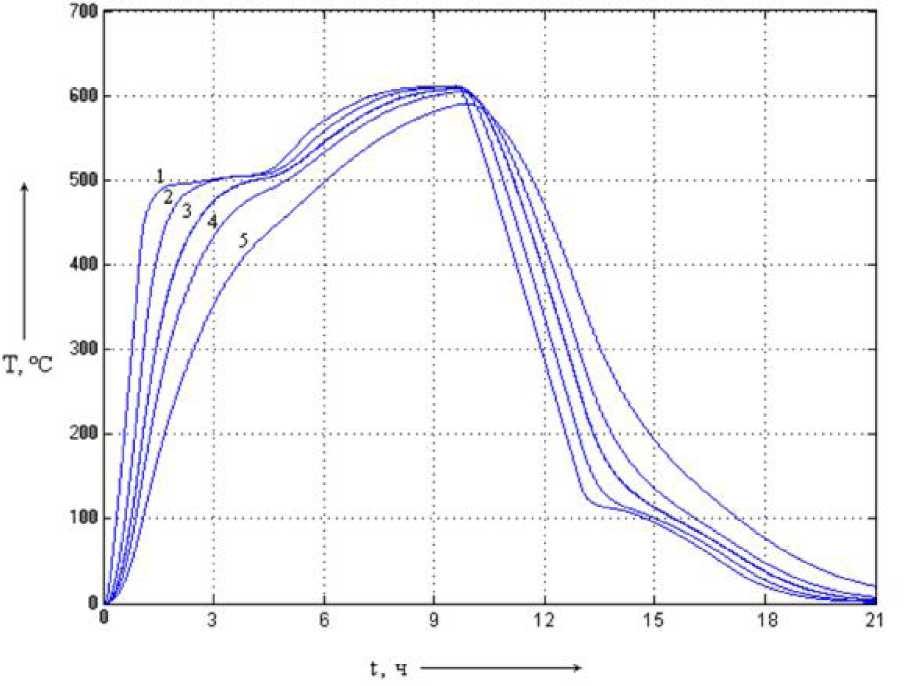

постоянной времени Т1; 2 - при постоянной времени 10Т1; 3 - при постоянной времени 20Т1; 4 - при постоянной времени 30Т1; 5 - при постоянной времени

50Т1)

Анализируя данные графиков, можно отметить, что в системе без НЛР с изменением Т₁ происходит замедление процессов в системе, а также меняется величина температурного рассогласования теплового поля уста­новки в начале и конце процесса прокаливания угля. При больших Т₁ ско-

170

рость нагрева понижается, не выдерживается продолжительность пребы­вания сырья при желаемой температуре от 450 до 550 °С.

Рис. 5.24. Динамические характеристики системы с однокаскадным нечётким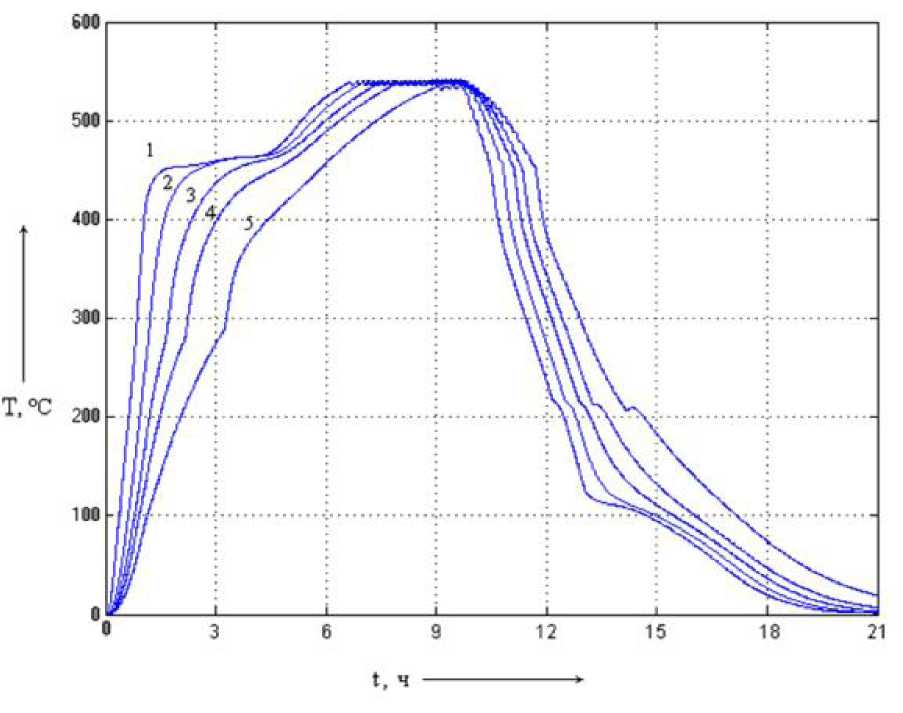

регулятором (1 - при постоянной времени Ті, 2 - при постоянной времени 10 Ті, 3 - при постоянной времени 20 Ті; 4 - при постоянной времени 30 Ті; 5 - при

постоянной времени 50 Ті)

Анализ результатов моделирования показывает, что введение нечёт­кого управления несколько повышает стабилизацию температурного поля (рис. 5.24). Однако, как и в системе без НЛР с изменением Ті происходит замедление процессов в системе, а также меняется величина температур­ного рассогласования теплового поля установки в начале и конце процесса прокаливания угля. При больших Ті скорость нагрева понижается, не вы­держивается продолжительность пребывания сырья при желаемой темпе­ратуре от 450 до 550 °С.

Применение однокаскадного НЛР позволяет удерживать конечную

температуру нагрева.

Рис. 5.25. Динамические характеристики системы с многокаскадным нечётким регулятором (1 - при постоянной времени Ті; 2 - при постоянной времени 10 Ті;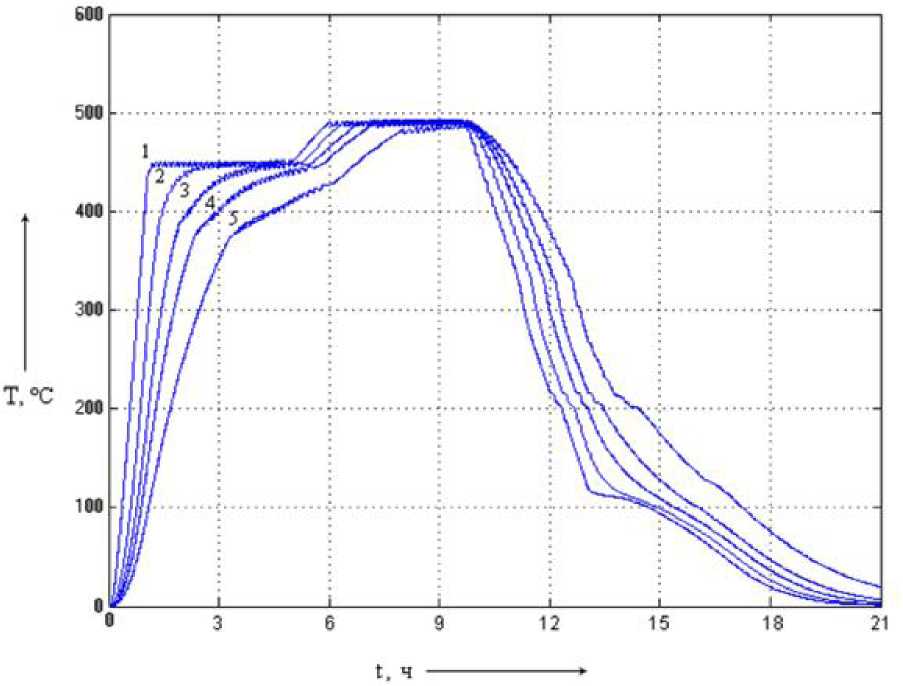

3. - при постоянной времени 20 Т_і; 4 - при постоянной времени 30 Т_і; 5 - при

постоянной времени 50 Ті)

Анализ результатов моделирования показывает, что введение нечёт­кого управления несколько повышает стабилизацию температурного поля. С изменением Ті происходит замедление процессов в системе, а также ме­няется величина температурного рассогласования теплового поля установ­ки в начале и конце процесса прокаливания угля. При больших Т₁ скорость нагрева понижается, не выдерживается продолжительность пребывания сырья при желаемой температуре от 450 до 550 °С (рис. 5.25).

Применение многокаскадного НЛР позволяет увеличить продолжи­тельность пребывания сырья при той или иной температуре и удерживать конечную температуру нагрева.

Рис. 5.26. Динамические характеристики системы с многокаскадным нечётким регулятором с раздельным управлением шторами с алгоритмом вывода Сугено/Мамдани (1 - при постоянной времени Ті; 2 - при постоянной времени 10Т/; 3 - при постоянной времени 20Ті; 4 - при постоянной времени 30Т_і; 5 -

при постоянной времени 50Т₁ )

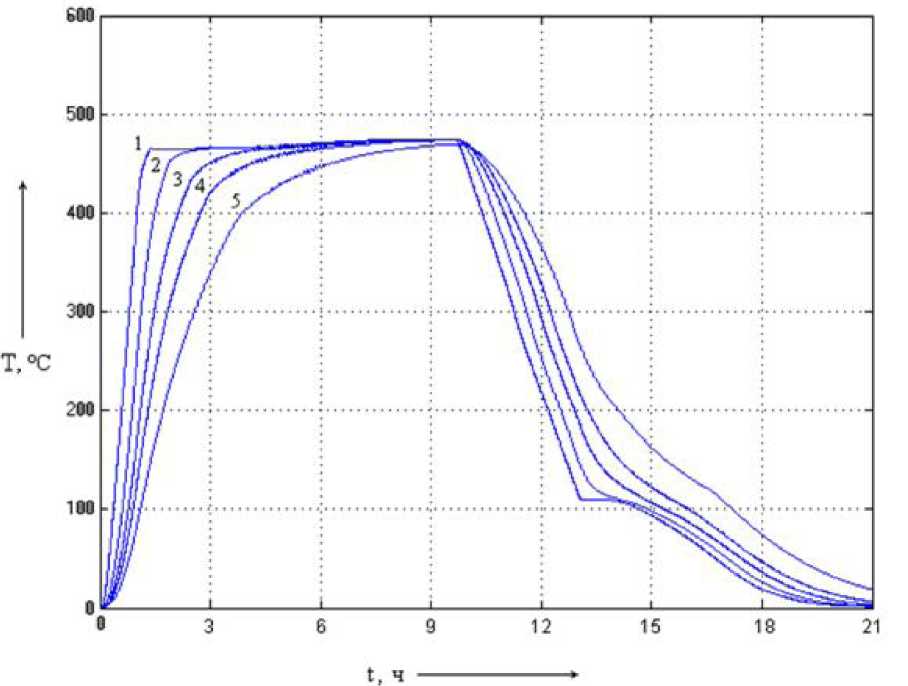
Анализ результатов моделирования показывает, что введение нечёт­кого управления несколько повышает стабилизацию температурного поля. С изменением Т_і происходит замедление процессов в системе, однако ве­личина температурного рассогласования теплового поля установки в нача­ле и конце процесса прокаливания угля меняется незначительно (рис. 5.26). Применение многокаскадного НЛР позволяет увеличить про­

должительность пребывания сырья при температуре от 410 до 470 °С и удерживать конечную температуру нагрева, т.е. в данном случае примене­ние многокаскадного НЛР с раздельным управлением шторами обеспечи­вает уменьшение чувствительности к изменению параметров системы и некоторое улучшение качества регулирования.

Рис. 5.27. Динамические характеристики системы с многокаскадным нечётким регулятором с раздельным управлением шторами с алгоритмом вывода Сугено/Сугено (1 - при постоянной времени Ті; 2 - при постоянной времени 10Т/; 3 - при постоянной времени 20Ті; 4 - при постоянной времени 30Т_і; 5 -

при постоянной времени 50Т₁)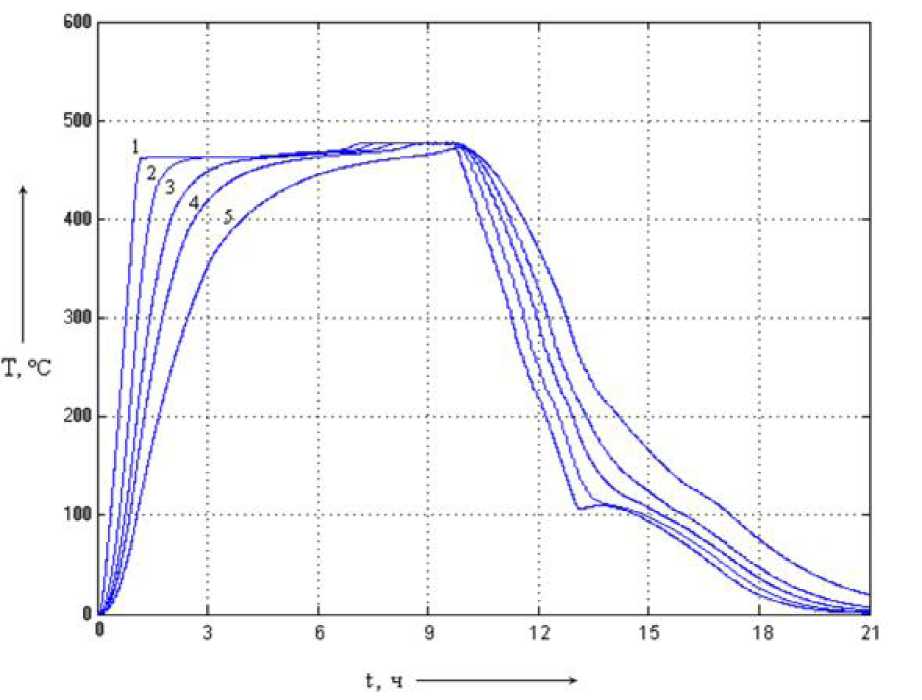

Анализ результатов моделирования показывает, что введение нечёт­кого управления несколько повышает стабилизацию температурного поля. С изменением Т_і происходит замедление процессов в системе, однако ве-

личина температурного рассогласования теплового поля установки в нача­ле и конце процесса прокаливания угля меняется незначительно. Примене­ние многокаскадного НЛР позволяет увеличить продолжительность пре­бывания сырья при температуре от 410 до 470 °С и удерживать конечную температуру нагрева (рис. 5.27), т.е. в данном случае применение много­каскадного НЛР с раздельным управлением верхней и нижней шторами обеспечивает уменьшение чувствительности к изменению параметров си­стемы и некоторое улучшение качества регулирования.

Для оценки влияния постоянной времени первого апериодического звена на переходный процесс построим сводную характеристику для тем­пературы в точке начала экзотермической реакции (4-5 ч) в зависимости от Т1 (рис. 5.28).

Рис. 5.28. Зависимость температуры начала экзотермической реакции от Т1 (1 - система без НЛР; 2 - система с однокаскадным НЛР; 3 - система с многокаскадным НЛР с алгоритмом вывода Мамдани/Мамдани; 4 - система с многокаскадным НЛР с алгоритмом вывода Сугено/Мамдани с раздельным управлением шторами; 5 - система с многокаскадным НЛР с алгоритмом вывода Сугено/Сугено с раздельным управлением шторами)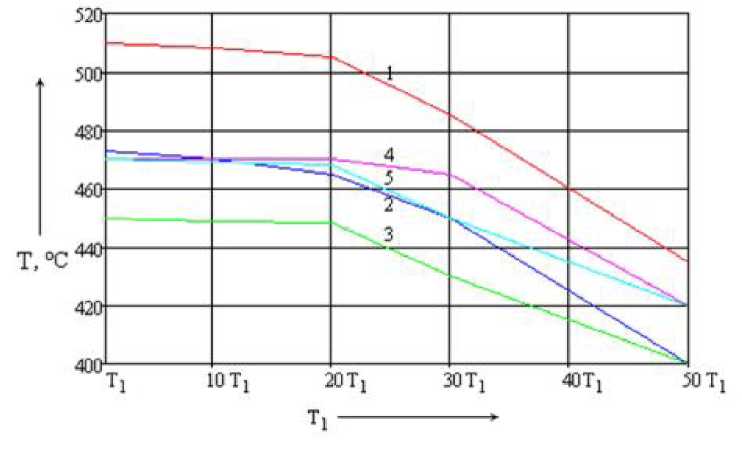

Как было отмечено ранее, в каждом режиме пиролиза надо выдержи­вать скорость нагрева, продолжительность пребывания сырья при той или

175

иной температуре, её значение, конечную температуру нагрева. В системе без НЛР и с любым из четырех нечётких регуляторов с изменением Т] происходит замедление процессов. При больших Т_] скорость нагрева по­нижается, не выдерживается продолжительность пребывания сырья при желаемой температуре от 450 до 550 °С. Но системы с НЛР позволяют уменьшить величину температурного рассогласования теплового поля установки в начале и конце процесса прокаливания угля, удержать конеч­ную температуру нагрева и увеличить время пребывания сырья в желае­мом температурном диапазоне. В системах с НЛР точка начала экзотерми­ческой реакции смещается в пределах 50...70 °С, тогда как в исходной си­стеме это смещение достигает 100 °С. В системах с НЛР с раздельным управлением шторами все процессы наиболее приближены к технологии пиролиза.

Анализируя результаты моделирования системы при различных воз­мущениях, можно констатировать, что синтезированные НЛР придают си­стеме управления некоторые свойства робастности, т.е. пониженной чув­ствительности к изменениям параметра системы.

Сравнительный анализ результатов моделирования нечёткой систе­мы регулирования углевыжигательной печью с регулятором и без показал, что НЛР позволяет оптимизировать переходные процессы в системе за счет уменьшения температурного рассогласования на этапе экзотермиче­ского процесса и повысить качество выходной продукции - древесного уг­ля, т.к. процесс пиролиза протекает при более равномерном распределении температур. Использование НЛР наглядно демонстрирует улучшение ста­билизационных свойств системы на этапе пиролиза древесины, в против­ном случае температура (в системе без НЛР) выходит за пределы желае­мой температурной области.

Наиболее эффективным является НЛР с раздельным управлением верхней и нижней шторами с любым из алгоритмов вывода. НЛР с алго­ритмом вывода по Сугено позволяет добиться более равномерного распре­деления температур внутри камеры установки при существенном сокра­щении базы правил регулятора. При прочих равных условиях и при опти­мальных параметрах погрешность регулирования с применением алгорит­ма Сугено меньше, чем с применением алгоритма Мамдани.

НЛР способен компенсировать возникающие в объекте управления изменения параметров, что позволяет оптимизировать переходные процес­сы. При этом использование НЛР с алгоритмом нечёткого логического вы­вода Сугено является более предпочтительным, поскольку НЛР, построен­ный по такому алгоритму, лучшим образом осуществляет реализацию за­конов управления сложными объектами.

2. Синтез нечёткого многокаскадного ПИД-регулятора.

Применение нечёткой логики в управлении позволяет отказаться от создания достаточно точной математической модели динамической систе­мы и использовать лишь экспертные знания о поведении системы. В связи с этим рассмотрим применение нечёткого многокаскадного управления си­стемой с отрицательной обратной связью и ПИД - регулятором (рис. 5.29). В качестве входных измеряемых координат выбраны ошибка и производ­ная ошибки, в качестве выходной координаты - выход ПИД-регулятора.

Рис. 5.29. Система с отрицательной обратной связью и ПИД - регулятором

177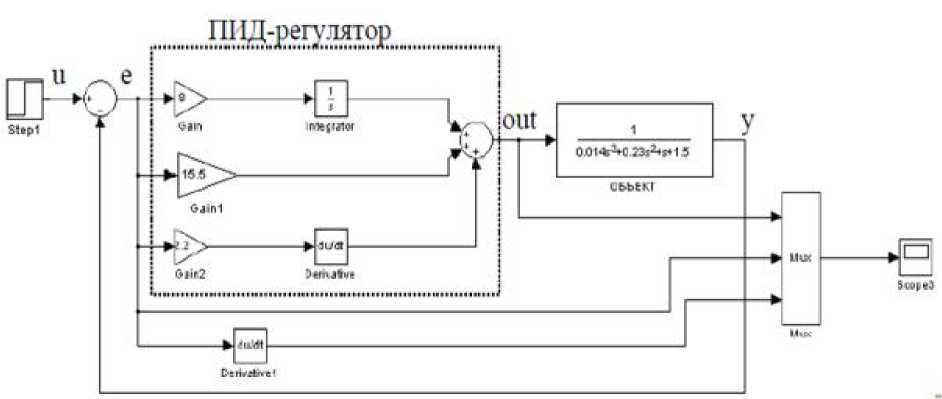

Объект управления представляет собой полином третьего порядка. Его передаточная функция К_о (я) имеет вид:

К (я) = ₃ ¹ ₂ .

0.014 • я³ + 0.23 • я² + я +1.5

Математическая модель системы с ПИД-регулятором исследована с точки зрения переходных процессов по «ошибке», «производной ошибки» и «выходу» при скачке сигнала задания и при неизменных параметрах объ­екта управления. Переходные процессы исследуемых величин приведены на рис. 5.30.

Рис. 5.30. Графики переходных процессов измеряемых величин ПИД-регулятора (1 - выход регулятора; 2 - ошибка; 3 - производная ошибки)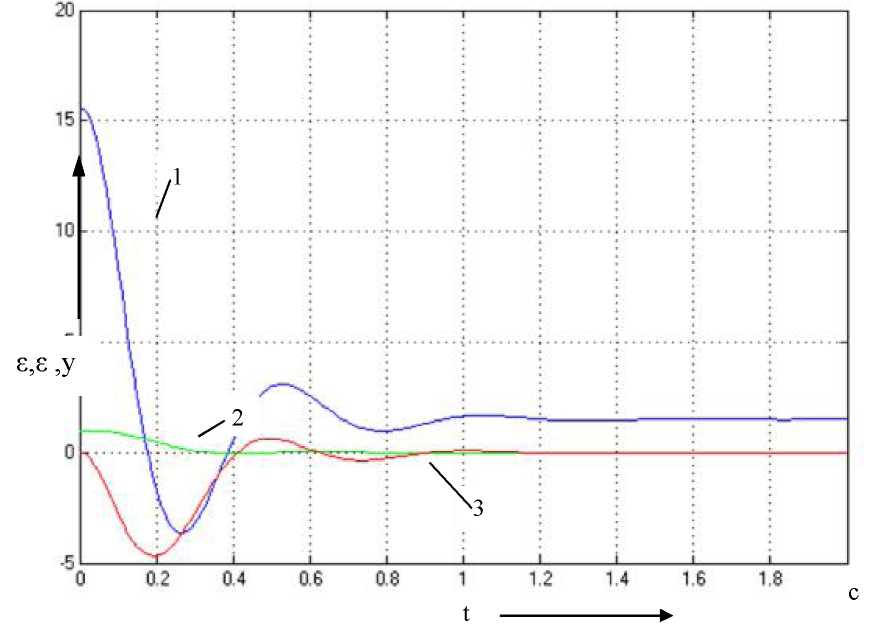

Основным недостатком приведённой системы стабилизации является сравнительно невысокая динамическая точность при действии недетерми­нированных возмущений и изменениях параметров объекта управления. Для повышения динамической точности целесообразно использовать в си­стеме регулирования вместо ПИД-регулятора нечёткие логические регуля­торы.

В пользу НЛР может выступать и то, что хорошо настроить ПИД- регулятор на практике достаточно сложно. Поиск хороших ПИД настроек - процесс во времени длительный. Хорошо если инженер имеет специаль­ные компьютерные программы, позволяющие ему искать правильные ре­шения эффективно и с минимальными временными затратами, но на прак­тике это не всегда так. Поэтому для ослабления влияния отмеченных фак­торов попробуем интеллектуализировать систему управления за счёт вве­дения НЛР.

5.2.1 Синтез нечёткой системы управления

Нечёткая система управления представляет собой три нечётких регу­лятора установленных соответственно в пропорциональном, интегральном и дифференциальном каналах ПИД-регулятора (Рис. 5.31).

Рис. 5.31. Структурная схема нечёткой системы управления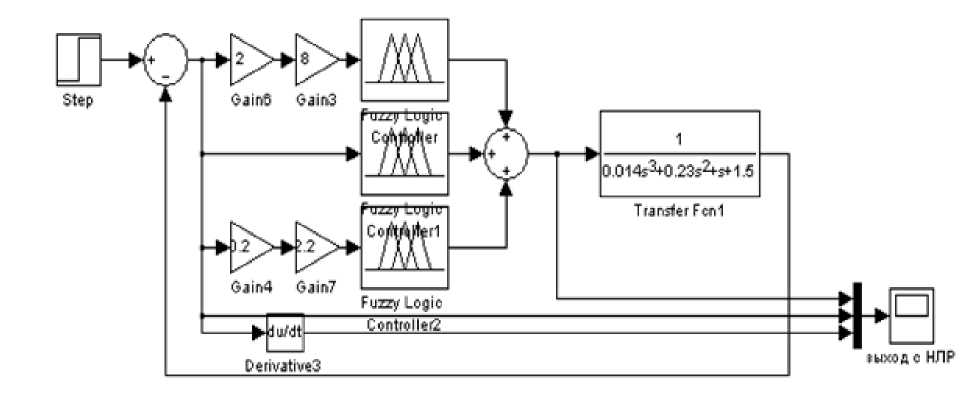

При синтезе нечёткого регулятора будем применять алгоритм нечёт­кого логического вывода Сугено, для которого характерна эффективность в вычислительном отношении, высокая линейная сходимость, а также су­щественная формализация.

Настройка НЛР осуществляется в соответствии со структурной схе­мой приведённой на рис. 5.30. Средством, позволяющим связать любую физическую величину с каким-либо множеством, качественно характери­зующим её значения, является лингвистическая переменная. Введем линг­вистическую переменную «ошибка» (е). Для всех внутренних термов, входной переменной, назначим треугольные функции принадлежности.

Учитывая, что к виду переходной характеристики системы не предъ­являются специальные требования, для снижения алгоритмической слож­ности базы знаний нечёткого контроллера базовое терм-множество вход­ных лингвистических переменных ограничим на уровне пяти. Терм мно­жество - Т лингвистических переменных - имеет название термов: Т={Б, РБ, РМ, РВ, РУБ), означающее соответственно: «малое», «положительное малое», «положительное среднее», «положительное большое», «положи­тельное очень большое».

Количественные характеристики функций принадлежности опреде­лим в зависимости от диапазона изменения параметра, для которого стро­ятся функции принадлежности его термов. Они могут быть получены либо из экспериментальных данных, либо из результатов моделирования, но в любом случае они должны действительно влиять на систему. В работе диапазоны входных переменных получены по результатам моделирования ПИД-регулятора. Для входа регулятора диапазон изменения принят [-0.05, 1]. Вид термов для лингвистической переменной «ошибка» представлен на рис. 5.32.

Рис. 5.32. Функции принадлежности лингвистической переменной «ошибка»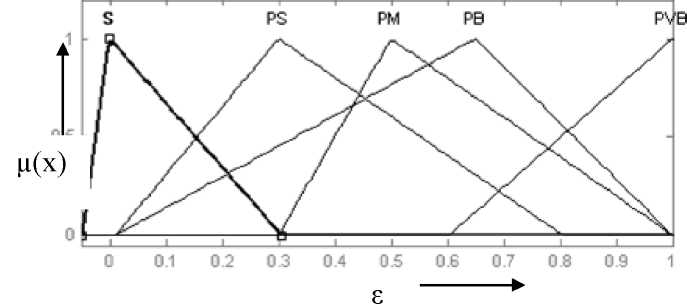

Терм-множество выходных лингвистических переменных ограничим на уровне трёх. Терм множество - Т1 лингвистических переменных - име­ет название термов: Т1=(КБ, РБ, РВ}, означающее соответственно: «отри­цательно малое», «положительное малое», «положительное большое».

Для выхода регулятора диапазон изменения параметров управляю­щего воздействия принят [-2; 6; 14,5].

Содержательным компонентом блока нечёткого вывода является ба­за знаний НЛР. Она строится исходя из цели применения НЛР.

В естественно-языковой вербальной форме управление будет иметь следующий вид:

Если сигнал ошибки положительный и возрастает, то управляющий сигнал будет - положительный малый. Если положительный сигнал ошиб­ки будет очень большой, то управляющий сигнал на выходов также будет расти, становясь положительным большим. Если сигнал ошибки будет па­дать, то выходной сигнал также будет падать.

Базу знаний нечёткого регулятора целесообразно формировать в ви­де ряда продукционных правил. Получим множество управляющих пра­вил, связывающих лингвистические значения входной и выходной пере­менных вида:

1) Если «ошибка» есть РВ, тогда «управление» есть РБ = 6,

2. «Если «ошибка» есть РУБ, тогда «управление» есть РВ = 14.5,

3. «Если «ошибка» есть PM, тогда «управление» есть № = -2,

4. 

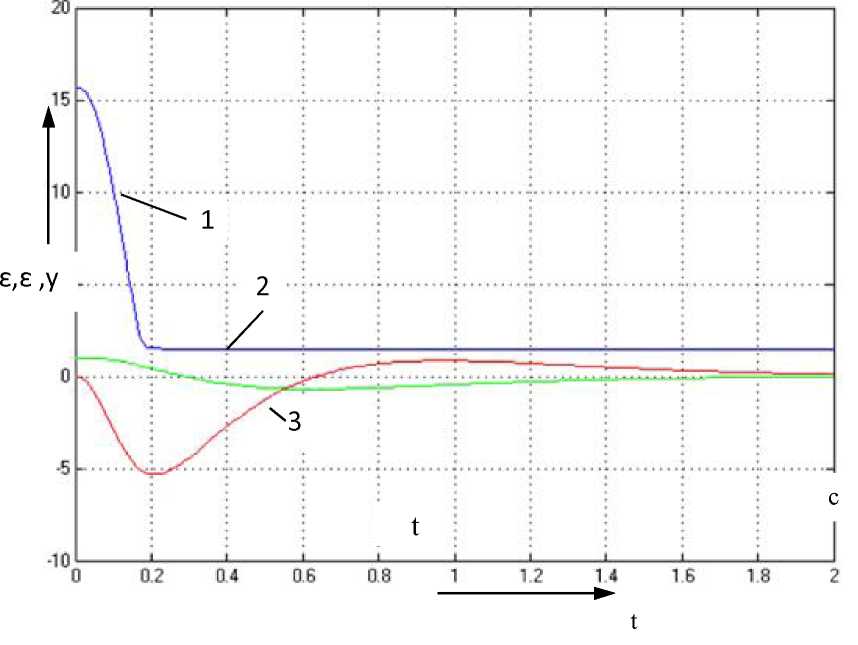
   Рис. 5.33. Графики переходных процессов измеряемых величин в системе с НЛР (1 - выход регулятора; 2 - ошибка; 2 - производная ошибки)

   «Если «ошибка» есть РS, тогда «управление» есть № = -2. Графики переходных процессов системы представлены на рис. 5.31

Результаты моделирования, приведённые на рис. 5.33, наглядно по­казывают правомерность применения НЛР. Полученная система обладает лучшими показателями качества, чем система с ПИД-регулятором. Дли­тельность переходного процесса уменьшилась в 6 раз. Использование ме­тодов нечёткого управления позволило получить качественный переход­ный процесс без использования громоздких вычислительных процедур, характерных для классического метода управления, хотя для улучшения

182

динамических характеристик и плавности выходного сигнала пришлось подбирать дополнительные коэффициенты усиления.

5.2.1 Нечёткая многокаскадная система управления

Структурно многокаскадная нечёткая система регулирования может быть реализована путём добавления дополнительного НЛР в систему при­ведённую на рис. 5.34. НЛР ставится последовательно в канал управления. Интеллектуальные свойства нечёткого регулятора дают возможность фор­мировать корректирующее воздействие на каждый локальный канал управления. Регулятор формирует корректирующие поправки заменяющие коэффициенты К1, К2 и КЗ ПИД - регулятора. Выходы НЛР подаются на вход НЛР построенного в предыдущем разделе, который соответственно вырабатывает управляющий сигнал сходный с управляющими воздействи­ями ПИД-регулятора, являющийся суммой трёх слагаемых. Структурная схема многокаскадной нечёткой системы регулирования представлена на рис. 5.34.

Рис. 5.34. Структурная схема многокаскадной нечёткой системы управления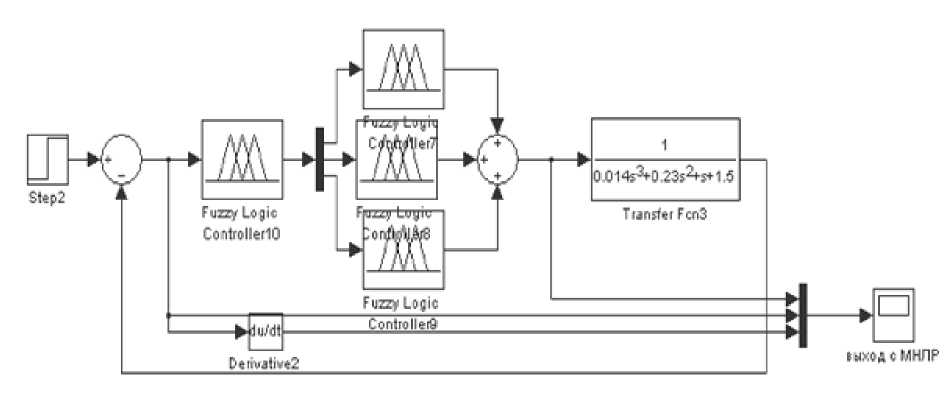

Данная система должна обеспечить формирование переходных ха­рактеристик рассматриваемых каналов близких к полученным в системе с ПИД-регулятором и в системе с НЛР (или улучшить эти характеристики).

Функциональная схема многокаскадного нечёткого логического регулято­ра приведена на рис. 5.35

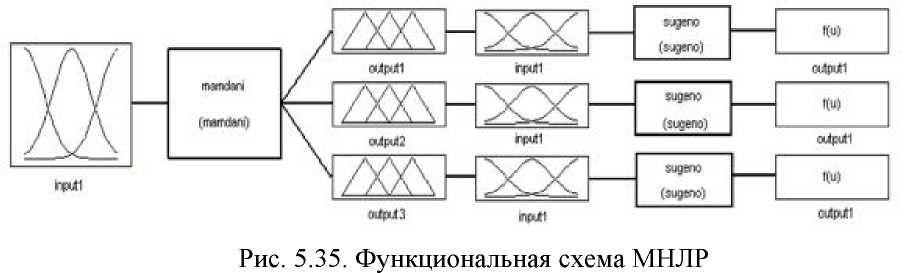
На нечёткое корректирующее звено возлагается задача выработки корректирующего воздействия в диапазоне изменения динамической ошибки системы стабилизации, при синтезе нечёткого регулятора исполь­зуем алгоритм вывода по Мамдани, как наиболее простой и интуитивный. Несмотря на то, что алгоритм Мамдани рекомендуют применять в других областях, а именно в экспертных системах и системах принятия решений, он может эффективно работать и в нашей нечёткой системе управления, что будет показано ниже.

Введём входную лингвистическую переменную «ошибкаї» (є1). Для всех внутренних термов, входной переменной, назначим треугольные функции принадлежности.

Учитывая, что к виду переходной характеристики системы не предъ­являются специальные требования, для снижения алгоритмической слож­ности базы знаний нечёткого контроллера базовое терм-множество вход­ных лингвистических переменных ограничим на уровне четырёх. Некото­рый произвол при выборе количества термов обусловлен тем, что при воз­растании количества термов возрастает объем базы правил, а существенно­го выигрыша в точности не наблюдается.

Терм множество - Т2 лингвистических переменных - имеет назва­ние термов: Т2=(К8, 7, РБ, РВ}, означающее соответственно: «отрица­тельное малое», «нулевое», «положительное малое», «положительное большое».

Количественные характеристики функций принадлежности опреде­лим в зависимости от диапазона изменения параметра, для которого стро­ятся функции принадлежности его термов. Диапазоны изменения парамет­ров были получены из результатов моделирования ПИД-регулятора. Для входа регулятора диапазон изменения принят [-0.7, 1]. Исходя из того, что данная входная переменная имеет 4 термы, получим следующие функции принадлежности, представленные на рис. 5.36.

Рис. 5.36. Функции принадлежности лингвистической переменной «ошибка 1»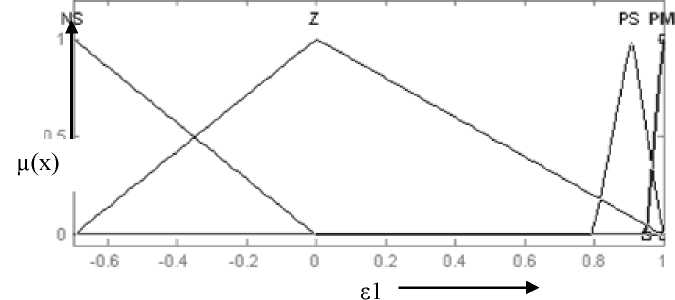

Введём выходные лингвистические переменные «коррекция 1» (у1) , «коррекция 2» (у2), «коррекция 3» (у3). Для всех внутренних термов, вы­ходных переменных, назначим треугольные функции принадлежности.

Диапазон изменения корректирующего воздействия взят с расчётом, чтобы управляющее воздействие действительно могло влиять на систему. Для каждого из трёх выходов он имеет своё значение.

Для снижения алгоритмической сложности базы знаний нечёткого контроллера базовое терм-множество выходных лингвистических пере­менных ограничим на уровне четырёх, также как и для входной лингви­стической переменной. Для трёх выходных сигналов зададимся тремя терм множествами - Т3, Т4, Т5 соответственно.

Рис. 5.37. Функции принадлежностей корректирующего воздействия первого

выхода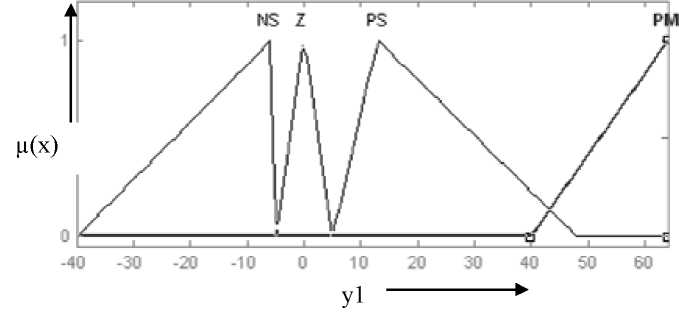

Рассмотрим первый выход НЛР. Терм-множество Т3 лингвистиче­ских переменных - имеет название термов: Т3=(КБ, 7, РБ, РВ}, означаю­щее соответственно: «отрицательное малое», «нулевое», «положительное малое», «положительное большое». Диапазон управляющего воздействия для этого выхода принят [-40, 64], а функции принадлежности корректи­рующего сигнала приведены на рис. 5.37.

Рис. 5.38. Функции принадлежностей корректирующего воздействия второго

выхода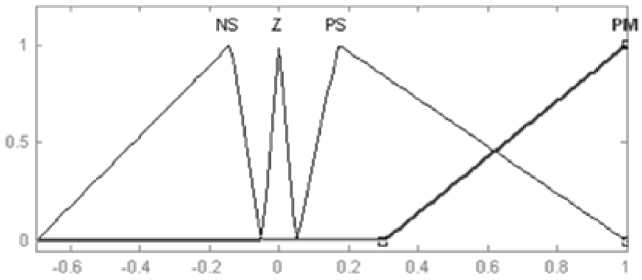

Второй выход НЛР. Терм-множество Т4 лингвистических перемен­ных - имеет название термов: Т4=(КБ, 7, РБ, РВ}, означающие соответ­ственно: «отрицательное малое», «нулевое», «положительное малое», «по-

ложительное большое». Диапазон управляющего воздействия [-0.7, 1]. Функции принадлежности приведены на рис. 5.38.

Третий выход НЛР. Терм-множество Т5 лингвистических перемен­ных - имеет название термов: Т5=(РБ, РМ, РВ, РУБ) означающие соответ­ственно: «положительное малое», «положительно среднее», «положитель­ное большое», «положительное очень большое». Диапазон управляющего воздействия [0.1, 1]. Функции принадлежности приведены на рис. 5.39.

Рис. 5.39. Функции принадлежностей корректирующего воздействия третьего

выхода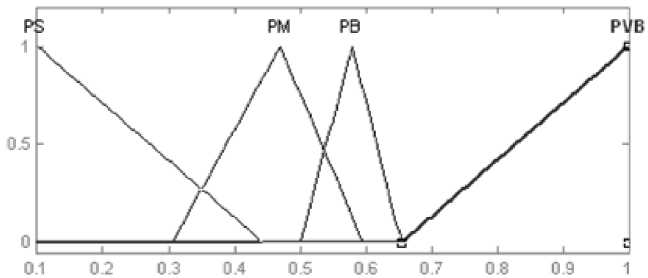

Содержательным компонентом блока нечёткого вывода является ба­за знаний НЛР. Для заполнения первоначально пустой базы знаний, необ­ходимо определить цели управления. Целью НЛР, как уже говорилось ра­нее, является корректировка сигнала управления.

Таким образом, будет обеспечиваться повышение быстродействия регулирующего воздействия и плавность изменения регулируемой величи­ны.

В естественно-языковой форме управление будет иметь следующий

вид:

Если сигнал ошибки положительный и возрастает, то корректирую­щий сигнал у первого и второго выходов регулятора будет - положитель­ный большой, а у третьего - положительный очень большой. Если поло­жительный сигнал ошибки уменьшается, то корректирующий сигнал для

187

всех выходов также будет уменьшаться, оставаясь положительным. Если сигнал ошибки нулевой, то корректирующий сигнал - отрицательный или положительный малый (третий выход). Если отрицательный сигнал ошиб­ки уменьшается по абсолютной величине, то корректирующий сигнал - нулевой или положительно средний (третий выход).

Базу знаний нечёткого регулятора целесообразно формировать в ви­де продукций. Получим множество управляющих правил, связывающих лингвистические значения входных и выходных переменных вида:

1. Если «ошибка 1» есть РВ, тогда «коррекция 1» есть РВ, «коррек­ция 2» есть РВ и «коррекция 3» есть РУБ;

2. Если «ошибка 1» есть Р8, тогда «коррекция 1» есть Р8, «коррек­ция 2» есть Р8 и «коррекция 3» есть РБ;

3. Если «ошибка 1» есть Ъ, тогда «коррекция 1» есть N8, «коррекция 2» есть N8 и «коррекция 3» есть Р8;

4. Если «ошибка 1» есть N8, тогда «коррекция 1» есть Ъ, «коррекция 2» есть Ъ и «коррекция 3» есть РМ.

Для рассматриваемой системы отсутствуют правила, содержащие анцендент с нулевой степенью принадлежности следовательно, можно сделать вывод о полноте правил управления.

Непротиворечивость системы управляющих правил обычно тракту­ется как отсутствие правил, имеющих сходные посылки и различные или взаимоисключающие следствия. Следовательно, можно судить о непроти­воречивости системы управляющих правил.

Проверим созданную базу знаний нечёткого регулятора и рассмот­рим переходный процесс системы с МНЛР. Графики переходных процес­сов системы представлены на рис. 5.40.

Рис. 5.40. Графики переходных процессов измеряемых величин в системе с

МНЛР (1 - выход регулятора; 2 - ошибка; 3 - производная ошибки)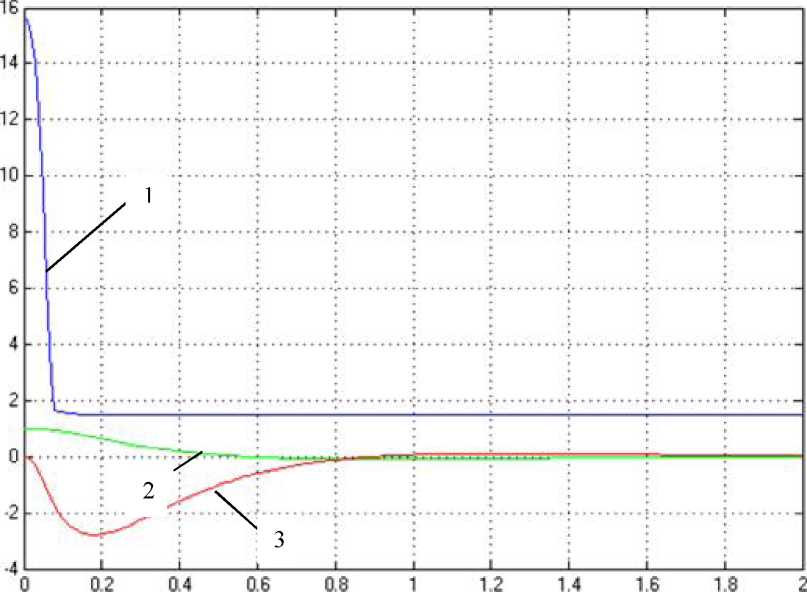

Из графика видно значительное уменьшение времени переходного процесса в системе с многокаскадным нечётким регулятором, по сравне­нию с классической системой и системой с НЛР. Длительность переходно­го процесса уменьшилась в 10 раз по сравнению с классической системой и в 2 раза по сравнению с системой с НЛР. Использование многокаскадно- сти в управлении позволило получить качественный переходный процесс без использования громоздких вычислительных процедур, необходимых для улучшения динамических характеристик как в классическом методе управления так и в нечёткой системе управления.

2. Сравнение систем, построенных с использованием различных методов

Рассмотрим динамические характеристики систем построенных с использованием различных методов.

На рис. 5.41 представлены переходные функции различных систем на выходе регуляторов.

Рис. 5.41. Графики переходных характеристик исследуемых систем на выходе регуляторов (1 - передаточная функция ПИД-регулятора; 2 - передаточная функция НЛР; 3 - передаточная функция МНЛР)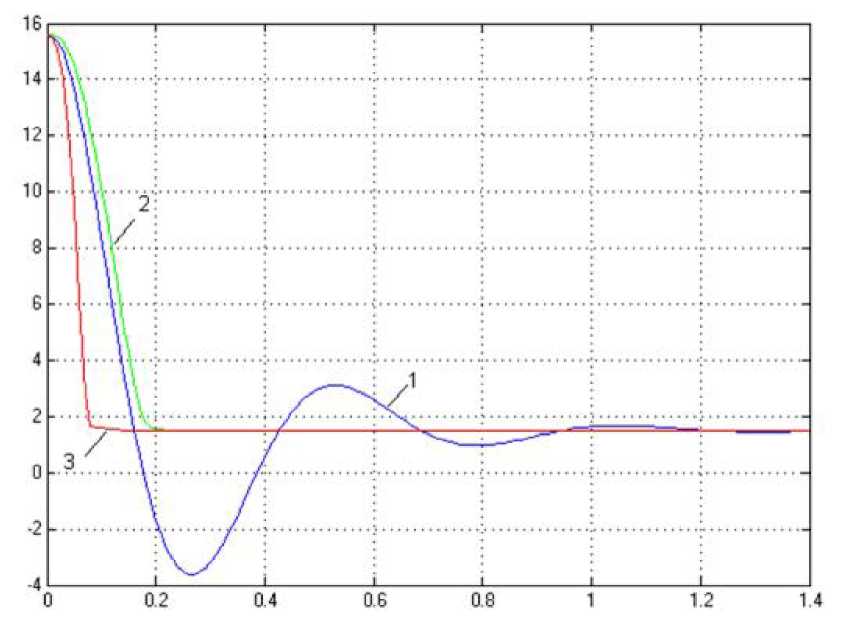

По результатам моделирования можно судить о заметном улучшении динамики системы. Результаты моделирования показывают значительное уменьшение времени переходного процесса систем построенных с исполь­зованием нечёткой логики. Для сравнения на рис. приведены три графика переходных процессов системы с ПИД-регулятором, с нечётким регулято­ром, а также система с многокаскадным нечётким регулятором. Переход­ный процесс классической системы является более затянутым и составляет

2. с. Быстродействие системы с НЛР в 6 раз выше, чем у классической (составляет 0,2 с), а системы с МНЛР в 10 раз (составляет 0,12 с).

Проведём сравнение реакции систем на различные воздействия (ва­риация параметров системы, возмущающих воздействий).

Рассмотрим влияние изменения параметров объекта управления пу­тем варьирования постоянной времени Т=0,23 в пределах ± 10%. Рассмот­рим изменение переходных процессов для различных систем.

Переходные процессы классической системы с ПИД-регулятором представлены на рис. 5.42.

Рис. 5.42. Графики переходных характеристик системы с ПИД-регулятором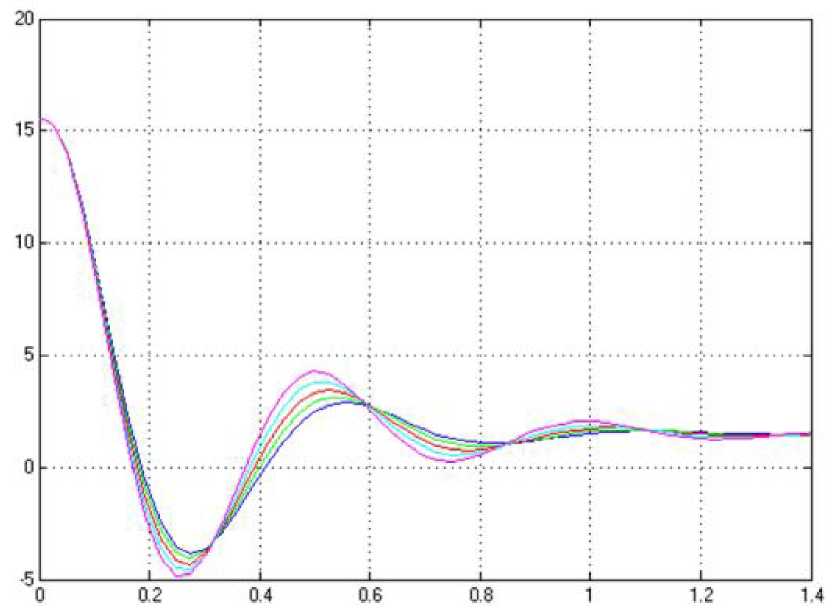

Переходные процессы системы с нечётким регулятором представле­ны на рис. 5.43.

Рис. 5.43. Графики переходных характеристик системы с НЛР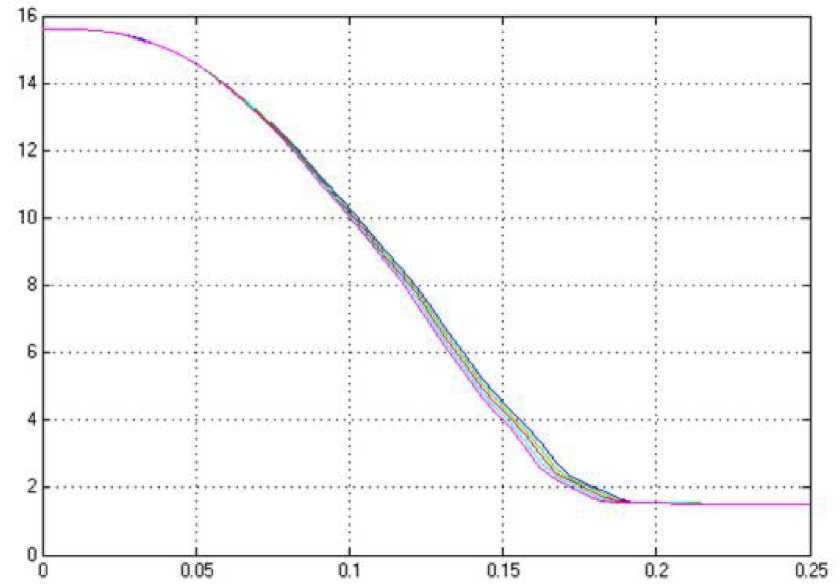

Рис. 5.44. Графики переходных характеристик системы с МНЛР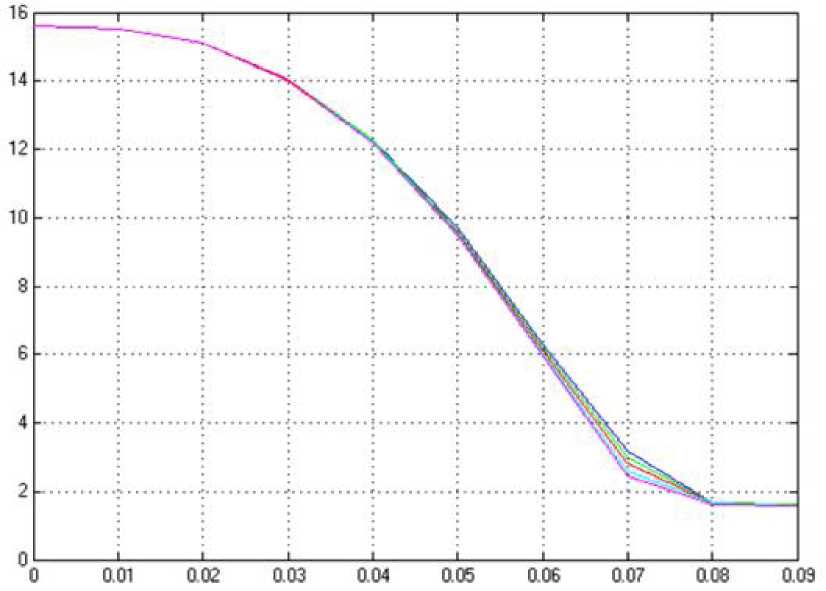

Переходные процессы исходной системы с многокаскадным нечёт­ким регулятором представлены на рис. 5.44.

Из графиков видно, что система с ПИД-регулятором практически не чувствительна к изменению параметра Т. Хотя, с увеличением этого коэф­фициента, увеличивается колебательность системы. С уменьшение наобо­рот снижается колебательность, и

характеристики для системы с ПИД- регулятором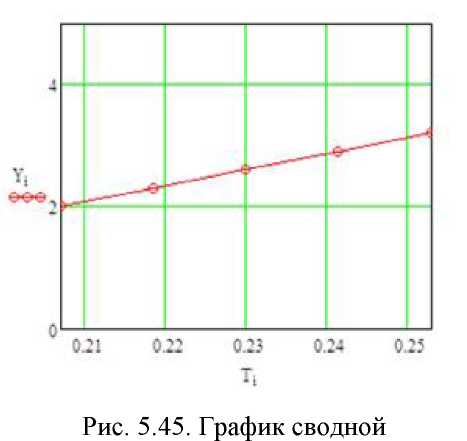

улучшается быстродействие. Изме­нение Т в системах с НЛР и с МНЛР не влияет на их показатели качества. Таким образом положительный эф­фект от использования нечётких ре­гуляторов достаточно ярко проявля­ется при изменении параметров си­стемы. Особенно у системы с МНЛР.

характеристики для системы с НЛР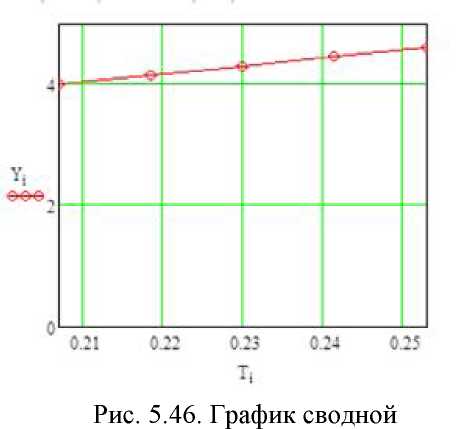

Представим зависимость вы­ходного сигнала от увеличения по­стоянной времени Т в период време­ни 7=0,15 с. Сводная характеристика для классической системы изобра­жена на рис. 5.45.

Сводная характеристика для системы с НЛР изображена на рис. 5.46, а для системы с МНЛР представлена на рис. 5.47.

Графики, приведённые на ри­сунках 5.44-5.47, ещё раз доказыва­ют преимущества многокаскадной системы. Изменение постоянных параметров никак не влияет на величину выходной переменной в системе с МНЛР, в то время как в других исследу­емых системах это изменение вполне заметно.

Подадим возмущающее воздействие на каждую из представленных систем. Переходные процессы представлены на рис. 5.48.

0.Л 0.22 из 0.24 0.25

Рис. 5.47. График сводной характеристики для системы с МНЛР

Из графика видно, что система с НР отрабатывает возмущающее воздействие лучше, чем система с ПИД-регулятором, а система с МНЛР невосприимчива к возмущению заданной величины. Следовательно, по­вышение интеллектуальности си­стемы управления позволяет по­высить её робастные свойства. Добавление ещё одного нечёткого регулятора позволяет снизить ве­личину статической ошибки.

Таким образом, можно сде­лать вывод, что регуляторы, по­строенные по алгоритмам пред­ставленным в работе, выполняют наложенные на них требования:

- обеспечивают необходи­мый закон управления;

• качественные показатели нечёткой системы управления удовлетво­ряют заданным требованиям;

• регулятор реализуем, т.е. его алгоритмическая сложность не очень громоздкая;

Рис. 5.48. Графики переходных процессов исследуемых системы при подаче возмущающего воздействия: (1 - передаточная функция ПИД-регулятора; 2 - передаточная функция НЛР; 3 - передаточная функция МНЛР)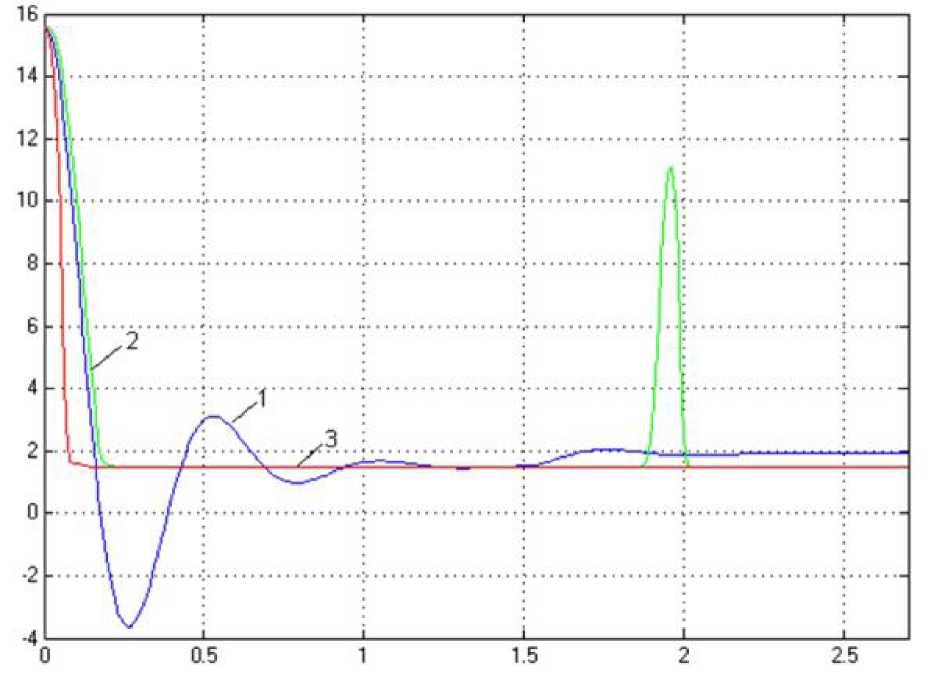

При этом сама система управления обладает определёнными свой­ствами. Она «слабочувствительна» к неточности математического описа­ния объекта регулирования, к вариациям его параметров, а также к подаче недетерминированных возмущений, имеет возможность интерпретировать качественные характеристики параметров регулирования в количествен­ные. Кроме того, повышение интеллектуальности системы приводит к су­щественному увеличению её быстродействия, не снижая динамическую точность.