Глава 4. Принципы компенсации нелинейностей систем управления на основе нечёткого подхода

В теории автоматического управления при исследовании динамиче­ских режимов систем регулирования принято замкнутую систему регули­рования разбивать на ряд звеньев, взаимодействующих друг с другом в процессе функционирования системы. При этом всегда стремятся (когда это допустимо) описать звенья линейными уравнениями, что в конечном итоге является определённой идеализацией математического описания ре­альных устройств и позволяет при исследовании опираться на линейные методы анализа и синтеза систем регулирования, которые широко и глубо­ко проработаны. Но не все реальные звенья поддаются приемлемым спо­собам линеаризации без условия потери ряда важных свойств при исследо­вании систем регулирования. В таких случаях некоторые звенья в системе регулирования приходится описывать нелинейными уравнениями и при исследовании систем использовать специальные приёмы и методы, напри­мер метод гармонической линеаризации подробно освещённый в [64]. Все разнообразие нелинейных уравнений и подробная классификация нели­нейных звеньев приведена в [59].

В самом широком аспекте все нелинейности в системах автоматиче­ского регулирования условно можно разделить на естественные и искус­ственные. Естественные нелинейности возникают как результат конструк­тивных особенностей и принципа действия тех или иных элементов систе­мы. Среди естественных наиболее часто встречаются нелинейности типа зоны нечувствительности, насыщения, люфта, а также сложные нелиней­ности, представляющие то или иное сочетание типовых нелинейностей. Искусственные нелинейности специально вводятся в систему с целью до­стичь определённых динамических свойств системы или упростить её кон­струкцию.

Естественные нелинейности, как правило, оказывают отрицательное влияние на динамические свойства систем автоматического управления, ограничивают возможности повышения их точности. Из-за наличия есте­ственных нелинейностей возникают дополнительные погрешности, увели­чивается время переходного процесса, возможна также потеря устойчиво­сти системы.

Другой подход, приводящий к линеаризации системы регулирования в целом, связан с использованием различных компенсирующих устройств и специальных методов и приёмов [64]. Следует отметить, что на практике компенсация нелинейностей в ходе автоматического управления техноло­гическими процессами происходит в условиях неопределённости, связан­ной с отсутствием достаточной статистики о поведении управляемых объ­ектов. Проектировщикам систем управления такими объектами приходит­ся учитывать не формализуемые или трудно формализуемые факторы. Уровень сложности подобных систем настолько высок, что использование известных детерминированных и стохастических моделей для их проекти­рования не всегда обеспечивает получение желаемых характеристик. В этих случаях адекватные математические модели управляемых систем мо­гут основываться на теории нечётких множеств, позволяющей синтезиро­вать интеллектуальные системы управления.

4.1. Метод компенсации естественных нелинейностей с использованием статических характеристик нелинейностей

Предлагается задачу компенсации нелинейных свойств объектов ре­гулирования перенести в область нечётких отношений. Постановка и ре­шение этой задачи базируется на принципах нечётких множеств [33 - 36] и теореме о нечёткой аппроксимации [11]. Для автоматизации процесса син­теза базы знаний нечёткого логического регулятора, используемого в каче­стве компенсатора, и исключения субъективного фактора [8, 9] при этом предлагается метод синтеза регулятора с использованием статической ха­рактеристики нелинейности.

Полагая, что для рассматриваемого диапазона входных воздействий компенсируемый нелинейный элемент является безынерционным, и, учи­тывая тот фактор, что большинстве случаев влияние нелинейного элемента на проходящий через него сигнал можно оценить путём «съёма» его стати­ческой характеристики (тогда как получение аналитического выражения зачастую является задачей нетривиальной), а желаемый вид выходного сигнала нелинейного элемента представляет собой входной сигнал по­следнего, можно предложить метод синтеза нечёткого логического регуля­тора, включающий в себя следующие этапы [57]:

1. формулировка задач компенсации и определение требований к каче­ству;

2. определение возможных вариантов компенсации (способов подачи компенсирующего воздействия);

3. выбор оптимального варианта компенсации;

4. съем статической характеристики нелинейного элемента;

5. построение модели нечёткого логического регулятора (фаззифика- ции входных переменных, дефаззификации выходной и формирования ба­зы нечётких правил);

6. проверка адекватности полученной модели;

7. техническая реализация нечёткого логического регулятора на ос­нове полученной модели.

На первом этапе согласно предлагаемому методу необходимо сфор­мулировать задачу компенсации исследуемой системы (нелинейного эле­мента) и определить требования к качеству этой компенсации.

На втором этапе, исходя из требований, полученных на предыдущем этапе, необходимо определить способ подачи в исследуемую систему ком­пенсирующего воздействия.

Структурно включение компенсирующего устройства (нечёткого ло­гического регулятора (функции) можно реализовать по трём вариантам:

1. Введение компенсирующей прямой связи с нечётким логическим регулятором с подачей сигнала коррекции на вход нелинейности (рис. 4.1);

2. Введение компенсирующей обратной связи с нечётким логиче- ским регулятором с подачей сигнала коррекции на вход нелинейности (рис. 4.2);

3. Введение компенсирующей прямой связи с нечётким логическим регулятором с подачей сигнала коррекции на выход нелинейности (рис. 4.3).

Рис. 4.1. Структурная схема компенсации введением ком­пенсирующей прямой связи с нечётким логическим регу­лятором с подачей сигнала коррекции на вход нелинейно­ _і ф

сти (^_НЛР - нечёткая логическая функция; - нели­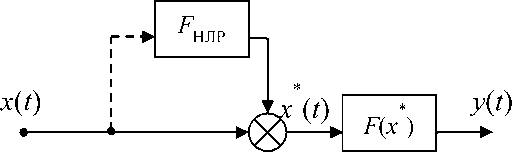

нейность; х(і) - входной сигнал; у( /) - выходной сигнал)

Рис. 4.2. Структурная схема компенсации введением компенсирующей обратной связи с нечётким логиче­ским регулятором с подачей сигнала коррекции на вход нелинейности (У_НЛР - нечёткая ло­гическая функция; Г( X*) - нелинейность; х(і) - вход­ной сигнал; у ( і I - выходной сигнал)

*

х(ґ)=х (і)

К

НЛР

^К(х) <)

хо

—►

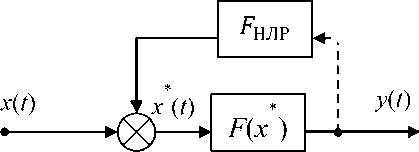
Рис. 4.3. Структурная схема компенсации введением компенсирующей прямой связи с нечётким логическим регулятором с подачей сигнала коррекции на выход нелинейности: . - нечёткая логическая функция;

I - нелинейность; х(і) - входной сигнал; у{!) - выходной сигнал

Согласно структурной схеме, представленной на рис. 4.1, имеем:

Г ^х *^(і) = ^{х (і)} + ^КНЛР,

1 у (і) = К (х*).

Тогда получаем:

^х *^(і) = ^{х (і)} + ^Кнлр ,

У (і) = К (х*).

Тогда:

У (*) = ^{Р (х)} + ^Рнлр •

Следует отметить, что для приведённых вариантов схемных решений не указаны аргументы нечёткой логической функции Р_НЛР и соответственно не показы входные сигналы нечёткого логического регулятора. Выбор кон­кретных анализируемых сигналов для реализации наиболее эффективной компенсации является отдельной задачей, решение которой зависит от вида нелинейности и технических требований к реализации. Рекомендуемыми сигналами для анализа в случае однозначной нелинейности являются вход­ной сигнал х^) для первого и третьего варианта, выходной сигнал у(1) - для второго. Для неоднозначных нелинейностей дополнительно к названным сигналам следует рассматривать производную входного сигнала по времени х'(().

На третьем этапе производится выбор оптимального варианта схемы компенсации. Предпочтительными являются либо первый, либо второй ва­риант, так как в случае, если нелинейностью обладает исполнительный ор­ган, реализация третьего варианта компенсации не только представляет существенные технические трудности, но и зачастую является невыполни­мой. Третий вариант схемы можно рекомендовать лишь для компенсации нелинейностей типа «насыщение», компенсация которых по первым двум вариантам невозможна.

На четвёртом этапе необходимо снять статическую характеристику корректируемой системы (нелинейного элемента). При этом следует стре­миться к минимизации интервала дискретности. Это обеспечит точность синтеза распределения терм-множеств входных и выходной переменных на следующем этапе и адекватность работы нечёткого логического регуля­тора в дальнейшем.

На пятом этапе производится построение модели нечёткого логиче­ского регулятора на основе результатов, полученных на предыдущих эта­пах. Для построения модели нечёткого логического регулятора (фаззифи-

106

кации входных переменных, дефаззификации выходной и формирования базы нечётких правил) предлагается использовать следующий алгоритм:

1. Если нелинейность является неоднозначной, то её статическая ха­рактеристика разбивается на однозначные участки вдоль оси абсцисс, для каждого из которых определяется интервал значений производной входно­го сигнала. Каждый из полученных интервалов задаёт носитель соответ­ствующего ему терм-множества (вид термов входной переменной, соот­ветствующей производной входного сигнала, рекомендуется выбирать треугольный, таким образом, чтобы множество было симметричным). В случае однозначной нелинейности, отсутствует необходимость нахожде­ния производной входного сигнала.

2. Для статической характеристики нелинейности проводится преоб­разование системы координат путём поворота осей последней на р/4 по ча­совой стрелке по следующей формуле [29]:

Ґ			0	р	>				0	р	\
х1	= х	cos				—	у	sin		—	5
			V	4	0				V	4	0
			0	р	\				0	р	\
У1 ч.	= х	sin	V	т	0	+	У	cos	V	4	0

(4.1)

где х и у - абсцисса и ордината соответственно точки статической характе­ристики в исходной системе координат; х₁ и у₁ - абсцисса и ордината точки статической характеристики в новой системе координат.

^у

0 Р '		0 р'
—	+ У1 • sin	—
V 4 0		V 4 0

х = х₁ • cos

0 рЛ		0 р'
—	+ У1 • sin	—
V 4 0		V 4 0

-х₁ • Sin

(4.2)

В новой системе координат определяются точки пересечения участка статической характеристики осью абсцисс, а также точки локальных экс­тремумов для каждого однозначного участка. Координаты найденных то­чек отображаются в исходную систему координат [29]:

В дальнейшем все действия выполняются в исходной системе коорди­нат.

3. Формируется распределения термов входного сигнала.

При реализации по первому варианту схемы координатами вершин терм-множеств входной переменной будут являться:

• абсциссы, полученные по формулам (4.2);

• абсциссы крайней правой и крайней левой точек каждого одно­значного участка статической характеристики.

При реализации по второму варианту схемы координатами вершин терм-множеств входной переменной будут являться:

• ординаты, полученные по формулам (4.2);

• ординаты крайней правой и крайней левой точек каждого одно­значного участка статической характеристики.

При реализации по третьему варианту схемы формирование терм- множеств аналогично первому.

Расположение границ интервала - носителя соответствующего терм- множества выбирается таким образом, чтобы они соответствовали верши­нам соседних терм-множеств. В случае крайних терм-множеств граница интервала выбирается таким образом, чтобы множество было симметрич­ным.

Если статическая характеристика нелинейного элемента (например, см. рис. 4.7) имеет линейные участки (параллельные оси абсцисс на преоб­разованной статической характеристике (см. рис. 4.11)) в области крайних входных терм-множеств (функций принадлежности), эти множества можно сделать 2- и ^-образного вида. Такой подход позволит сократить количе­ство входных функций принадлежности и как следствие выходных, и объ­ем базы знаний. Таким образом увеличиться быстродействие нечёткого ло­гического регулятора и упроститься техническая реализация.

Полученный набор термов является минимальным. В случаях, когда необходимо обеспечить повышенную точность компенсации, рекоменду­ется наряду с найденными абсциссами (ординатами) рассматривать допол­нительные абсциссы (ординаты). При этом можно вводить дополнитель­ные абсциссы (ординаты) как на определённом интервале, так и на всем диапазоне значений входной переменной. Во втором случае одним из ва­риантов для нахождения дополнительных абсцисс (ординат) является вы­числение среднего арифметического для каждой из пар соседних элемен­тов ранжированного ряда абсцисс (ординат), полученных в п.3. Таким об­разом, осуществляется фаззификация входных переменных.

4. Способ определения термов выходной переменной также зависит от выбранной ранее схемы реализации.

В случае реализации по первой схеме для каждой из точек, рассмот­ренных в п.3, находится разность между абсциссой точки статической ха­рактеристики, имеющей ординату равную абсциссе данной точки, и абс­циссой данной точки.

В случае реализации по второй схеме определение термов аналогич­но первой схеме.

В случае реализации по третьей схеме для каждой из точек, рассмот­ренных в п.3, находится разность между абсциссой и ординатой.

Найденные разности задают термы выходной переменной.

В зависимости от используемого алгоритма нечёткого вывода способ задания термов может отличаться. Так, например, при построении модели нечёткого логического регулятора по алгоритму Мамдани найденные раз­ности определяют синглтоны - нечёткие аналоги чётких чисел (в этом слу­чае степени принадлежностей для всех элементов универсального множе­ства равны нулю, за исключением одного со степенью принадлежности, равной единице). В случае же использования, например, алгоритма Сугено найденные разности задают функции-константы, в которых все коэффици­енты при входных переменных равны нулю.

5. При построении базы нечётких правил для каждого терма входной переменной x\=x, соответствующей входному сигналу (для однозначной статической характеристики), либо для каждой пары входных переменных xi=x и x₂=dxldt, соответствующей входному сигналу и его производной (для неоднозначной статической характеристики), и терму выходной пере­менной y=U строится правило нечёткой продукции вида:

If (x is «А») then (U is «С»)

(If (x is «А») and (dxldt is «В») then (U is «С»))

Т.е. в нашем случае для нечёткого логического вывода Мамдани:

где i=1 для однозначной нелинейности, i=2 в случае неоднозначной; <5/ - нечёткий терм, которым оценивается переменная x_t в j-м правиле; dj - за­ключение j-го правила; m - количество правил в базе знаний.

В случае если в базе нечётких правил обнаруживается пара правил, имеющих эквивалентную продукцию, а термы входной переменной заданы таким образом, что носитель соответствующего терм-множества в одном правиле включает носитель терм-множества в другом правиле, то правило, в котором используется терм, задающий более «узкое» терм-множество, исключается из базы.

Так как в правилах нечётких продукций в качестве логической связ­ки для подусловий (в случае неоднозначной нелинейности) применяется только нечёткая конъюнкция (операция «И» (and)), то в качестве метода агрегирования следует использовать операцию max - максимум. На нечёт­кую импликацию ограничений не накладывается; например, её можно про­

водить с использованием метода min - минимум. Дефаззификацию реко­мендуется проводить методом центра тяжести (взвешенное среднее). Введём обозначения:

mj (x_t) - функция принадлежности входа x_t е[x, x_t ] нечёткому терму

а , т.е. aj = J m,^(xi^)/xi;

x ^е[ x. X ]

ß_d (y) - функция принадлежности выхода y е y, у J нечёткому тер­^му dj. ^т.^е. dj = J m_dj ⁽у)ly.

у^е[^y .^y ]

Тогда в случае нечёткого вывода Мамдани, степень выполнения по­сылки j-го правила для текущего входного вектора X* = (x*, x*) рассчиты­вается следующим образом:

m, (^X' )=m, (^x*) x, m _у (^x*), J = i.^m,

где %j обозначает /-норму, так как в j-м правиле базы знаний используется

только логическая операция И (and).

В результате получаем нечёткое множество у, соответствующее

входному вектору X*:

„₂ * ⁽¹⁾ Для перехода от нечёткого множества, заданного на универсальном

множестве нечётких термов d₂,...,d_m} к нечёткому множеству на ин­

тервале | у,у | необходимо:

d,

d„

_у = mi(x*) + m₂(x *) +...+m _т (х *)

1. «срезать» функции принадлежности (У) на уровне т_й (X*);

2. объединить (агрегировать) полученные нечёткие множества. Ма­тематически это записывается следующим образом:

I тіп(т ^(х*Х⁽у))/у >

где - агрегирование нечётких множеств, которое наиболее часто реа­лизуется операцией нахождения максимума.

Чёткое значение выхода у, соответствующее входному вектору X* определяется в результате деффаззификации нечёткого множества у. Наиболее часто применяется дефаззификация по методу центра тяжести (взве­шенное среднее):

I у ■ т у⁽ у ¥у

У

у =

База знаний Сугено аналогична базе знаний Мамдани за исключени­ем заключений правил d_j, которые задаются не нечёткими термами, а ли-

нейной функцией от входов: = Ъ_]0 + ^ Ъ_]г ■ х_г . Правила в базе знаний Су- гено являются своего рода переключателями с одного линейного закона «входы-выход» на другой, тоже линейный. Границы подобластей размы­тые, следовательно, одновременно могут выполняться несколько линей­ных законов, но с различными степенями.

Таким образом, для случая нечёткого логического вывода Сугено:

где Ъ_{] 0} - некоторые действительные числа.

Степени принадлежности входного вектора X * =( х*, х*) к значениям d_j рассчитывается по формуле:

В результате получаем нечёткое множество у, соответствующее входному вектору X*:

Обратим внимание, что в отличие от результата вывода Мамдани (1), приведённое выше нечёткое множество является обычным нечётким мно­жеством первого порядка [9]. Оно задано на множестве чётких чисел. Ре­зультирующее значение выхода у определяется как суперпозиция линей­ных зависимостей, выполняемых в данной точке X* п - мерного фактор­ного пространства. Для этого дефаззифицируют нечёткое множество у, находя взвешенное среднее: £ Пй, (х *) • й,

У =

,=1, т

£ (X •)

,=1,т

или взвешенную сумму:

у = £ тй, ^(х*⁾ •.

,=1, т

На шестом этапе проводится проверка адекватности полученной мо­дели. Для более качественной проверки следует подавать на вход модели синусоидальный сигнал с амплитудой не меньше максимальной прогнози­руемой в процессе эксплуатации корректируемой системы. Желательно исследовать поведение модели на некотором интервале вероятных ампли­туд входного сигнала и оценить среднее квадратичное отклонение выход­ного сигнала корректируемой системы от требуемого. Если качество ком­пенсации нелинейности системы неудовлетворительное, следует повто­рить пятый этап метода, увеличив число терм-множеств входных перемен­ных при построении модели нечёткого логического регулятора по предла­гаемому алгоритму.

На седьмом этапе осуществляется техническая реализация нечёткого логического регулятора. При выборе аппаратной базы следует, прежде все­го, руководствоваться соображениями экономичности, т.к. модель, постро­енная по предлагаемому алгоритму, может быть реализована практически на любой аппаратной базе с общепромышленным управляемым контрол­лером.

Для придания нечёткому логическому компенсатору адаптивных свойств предлагается ввести в корректируемую систему измеритель рас­согласования, подающий управляющий сигнал ЭВМ при увеличении рас­согласования до неприемлемого уровня. В ЭВМ согласно алгоритму, опи­санному в методе на пятом этапе, производится синтез базы нечётких пра­вил, адекватной текущему состоянию системы. После этого производится настройка нечёткого логического компенсатора в соответствии с вновь сформированной базой правил. В настоящее время разработано достаточ­ное количество различных способов замены базы правил в процессе рабо­ты, например [31]. Ниже изображены варианты структурных схем, содер­жащие измеритель рассогласования и ЭВМ, для обеспечения адаптивности нечёткого логического компесатора при компенсации по первой схеме (рис. 4.4), на рис. 4.5 - по второй схеме, на рис. 4.6 - по третьей схеме со­ответственно.

В результате, будет обеспечиваться непрерывный контроль качества процесса компенсации, и осуществляться автоматическая подстройка не­чёткого логического компенсатора при изменении параметров корректиру­емого звена системы или уровня внешних воздействий.

Рис. 4.4. Структурная схема компенсации введением компенсирующей прямой связи с нечётким логическим регулятором с подачей сигнала коррекции на вход нелинейности: ИР - измеритель рассогласования

ИР

Рис. 4.5. Структурная схема компенсации введением компенсирующей обратной связи с нечётким логическим регулятором с подачей сигнала коррекции на вход нелинейности: ИР - измеритель рассогласования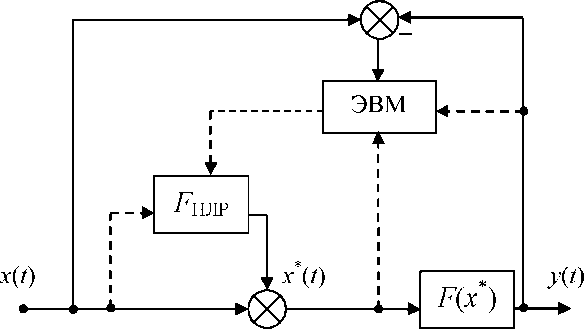

Рис. 4.6. Структурная схема компенсации введением компенсирующей прямой связи с нечётким логическим регулятором с подачей сигнала коррекции на выход нелинейности: ИР - измеритель рассогласования

Пример. Оценку эффективности предлагаемого метода выполним в среде инженерных вычислений Matlab пакет Simulink и Fuzzy Logic [16, 43,]. В данной среде была создана модель нелинейного элемента (рис. 4.7), имеющего статическую характеристику представленную на рис. 4.8.

Рис. 4.7. Функциональная схема нечёткого логического регулятора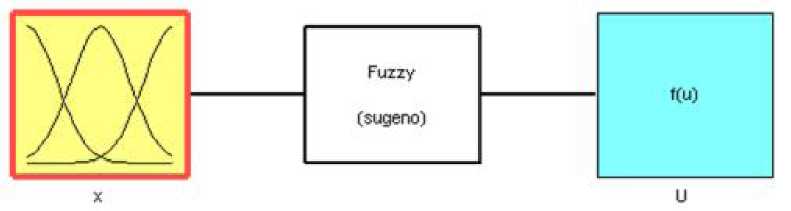

Структурная схема элементарной нелинейной системы, содержащей данный элемент, представлена на рис. 4.9, где Г(х) - некоторая априорно аналитически не определённая функция, описывающая нелинейный эле­мент со статической характеристикой, изображенной на рис. 4.8.

Проведём поэтапный синтез нечёткого логического регулятора для компенсации данной нелинейности по предлагаемому методу.

X

Рис. 4.8. Статическая характеристика нелинейного элемента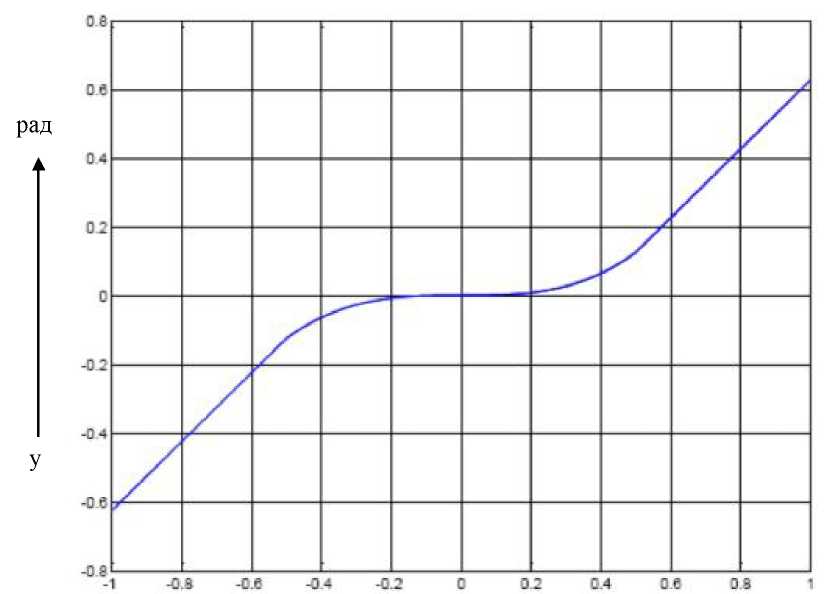

Первый этап. Пусть требуется компенсировать нелинейность систе­мы, изображённой на рис. 4.9. При этом среднее квадратичное отклонение выходного сигнала системы у(0 от входного х(?) не должно превышать 0,0025.

Рис. 4.9. Структурная схема элементарной нелинейной системы

Второй этап. В данном случае, возможно, реализовать любой из рас­сматриваемых вариантов подачи компенсирующего воздействия.

Третий этап. В качестве оптимального выберем первый вариант ком­пенсации.

Четвёртый этап. Снимем статическую характеристику (см. рис. 4.8). Так как каждому значению входного сигнала соответствует только одно

значение выходного, статическая характеристика однозначна. Следова­тельно, в качестве входного сигнала нечёткого логического регулятора бу­дем использовать входной сигнал системы. Тогда схема скомпенсирован­ной системы будет иметь следующий вид, представленный на рис. 4.10.

ИР

Рис. 4.10. Структурная схема скомпенсированной системы (RMS - блок определения среднего квадратичного отклонения; U(t) - сигнал управления; 6(t)

- ошибка (отклонение))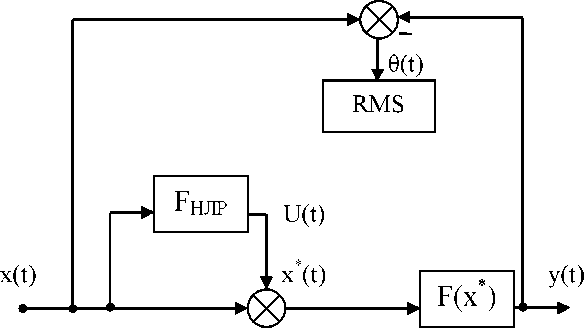

Пятый этап. Проведём построение модели нечёткого логического ре­гулятора по предлагаемому алгоритму.

1. Т.к. нелинейность является однозначной, не требуется проводить какого-либо дополнительного разбиения её статической характеристики на однозначные участки и использования производной входного сигнала.

2. Преобразуем систему координат статической характеристики по формулам (2). Результат этого преобразования представлен на рис. 4.11.

В новой системе координат находим точки пересечения участка ста­тической характеристики с осью абсцисс: (0; 0). Точки экстремумов стати­ческой характеристики: (0.4419; -0.2652), (-0.4419; 0.2652). В исходной системе координаты найденных точек согласно формулам (2.2) имеют вид: (0; 0), (0.5; 0.125), (-0.5; -0.125).

Рис. 4.11. Преобразованная статическая характеристика нелинейного элемента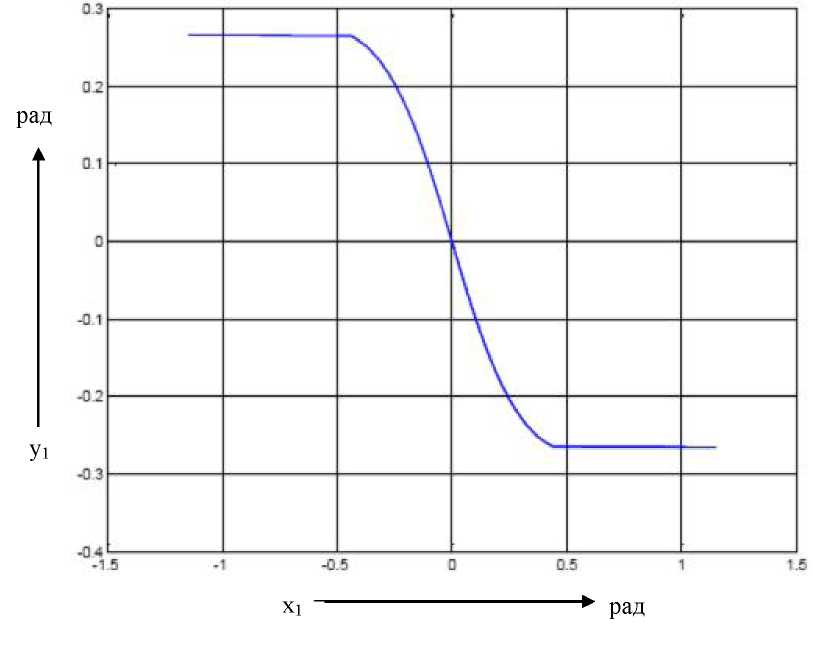

3. Определим термы входной переменной. Для этого найдём абсцис­сы крайней правой и крайней левой точек статической характеристики: (­1; -0.625), (1; 0.625). Учитывая абсциссы, полученные по формулам (2), получим следующий ряд абсцисс:

0, 0.5, -0.5, -1, 1

Для удобства ранжируем его:

-1, -0.5, 0, 0.5, 1

Таким образом получили координаты вершин терм-множеств вход­ной переменной, имеющие следующие названия x=(bos, sos, n, sps, bps}, означающие соответственно: bos - «большой отрицательный сигнал», sos - «средний отрицательный сигнал», mos - «малый отрицательный сигнал», n - «нулевой сигнал», mps - «малый положительный сигнал», sps - «средний положительный сигнал», bps - «большой положительный сигнал».

Следуя рекомендациям, приведённым в методе, получим распреде­ление терм-множеств входной переменной следующего вида (рис. 4.12).

Рис. 4.12. Распределение функций принадлежности входного сигнала нечёткого логического регулятора (х - входной сигнал; ц(х) - степень принадлежности

входного сигнала)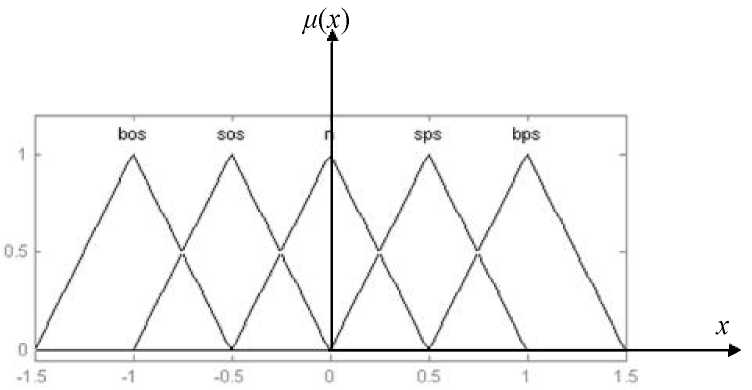

4. Определим термы выходной переменной. С этой целью для каж­дой из точек статической характеристики с абсциссами, названными в п. 3, находится разность между абсциссой точки статической характеристики, имеющей ординату равную абсциссе данной точки и абсциссой данной точки.

Например, для точки (-1; -0.625) находим разность между абсциссой точки (-1.375; -1) и абсциссой точки (-1; -0.625), т.е.

-1.375 - (-1)= -0.375

и т. д. для каждой из точек. В результате получим следующий ряд значе­ний:

-0.375, -0.375, 0, 0.375, 0.375

Среди этих значений встречаются одинаковые, которые в данном слу­чае, являются избыточными. Пусть алгоритмом нечёткого вывода будет ал­горитм Сугено нулевого порядка. Таким образом, термы выходной перемен­ной:

U={bos, n, bps}={-0.375, 0, 0.375}

Входные термы также преобразуются. Координатами вершин терм- множеств входной переменной будут: -0.5, 0, 0.5 имеющие следующие названия x={bos, n, bps}.

С учётом того, что статическая характеристика нелинейного элемен­та (см. рис. 4.7) имеет линейные участки (параллельные оси абсцисс на преобразованной статической характеристике (см. рис. 4.11)) в области крайних входных терм-множеств (функций принадлежности), эти множе­ства (bos, bps) можно сделать Z- и S'-образного вида:

Рис. 4.13. Распределение функций принадлежности входного сигнала нечёткого логического регулятора: х - входной сигнал; ц(х) - степень принадлежности

входного сигнала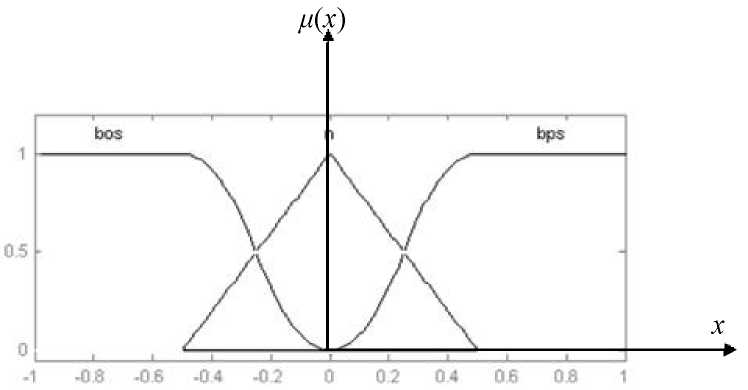

5. Составим базу правил (знаний) необходимой для выработки управляющих сигналов. При построении базы нечётких правил для каждо­го терма входной переменной, и функции-константе выходной переменной строится правило нечёткой продукции вида (4.3).

Таблица правил нечёткого логического регулятора:

1. If (х is bos) then (U is bos)

2. If (x is n) then (U is n)

3. If (x is bps) then (U is bps)

Очевидно, что в полученной базе нечётких правил нет пар правил, имеющих эквивалентную продукцию, где термы входной переменной за­даны таким образом, что носитель соответствующего терм-множества в одном правиле включает носитель терм-множества в другом правиле.

В качестве метода агрегирования будем использовать операцию max - максимум, в качестве нечёткой импликации применялся метод min - ми­нимум. Для дефаззификации используем метод wtaver - взвешенное сред­нее.

Шестой этап. Для оценки адекватности полученной модели был про­ведён анализ графиков входного и выходного сигналов(рис. 4.14) коррек­тируемой системы до и после подачи компенсирующего воздействия, а также сигналов по ошибке и управлению (рис. 4.15, 4.16). При этом, с це­лью изучения качества компенсации на всем диапазоне входных воздей­ствий на вход нелинейного элемента был подан синусоидальный сигнал (х=1 рад, щ=1 рад/с). В нескорректированной системе (рис. 4.9) средне­квадратичное отклонение выходной величины от входной было равно 0,3385. После подачи в систему компенсирующего предупреждающего воздействия (рис. 4.10) среднее квадратичное отклонение составило 0,06307.

Рис. 4.14. Графики переходных процессов входного и выходного сигналов корректируемой системы при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - без компенсирующего воздействия; 2 - с нечётким логическим регулятором; 3 - входной сигнал)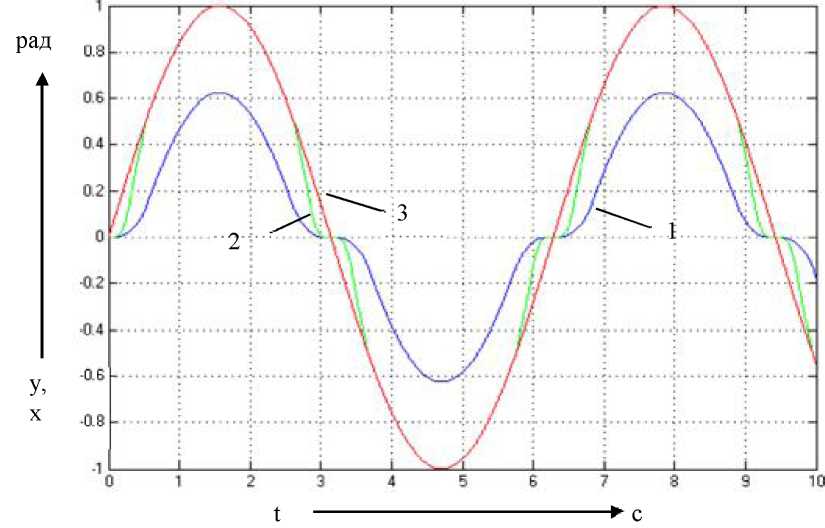

Рис. 4.15. Графики переходных процессов по ошибке при подаче на вход системы х=1 рад и частотой 1 рад/с: (1 - без компенсирующего воздействия; 2 -

с нечётким логическим регулятором)

123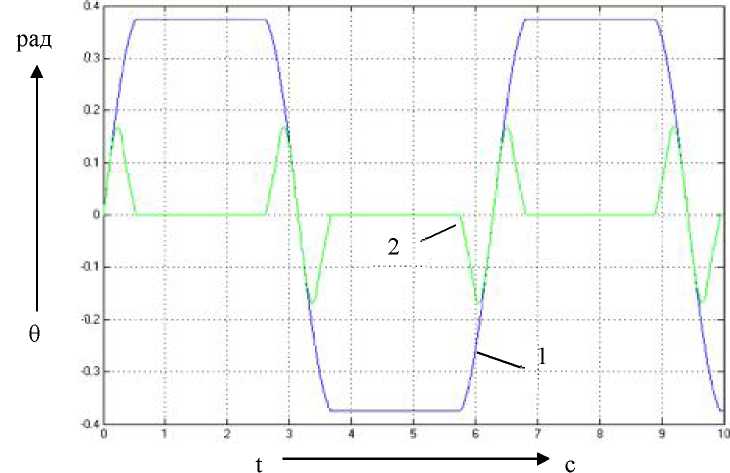

Рис. 4.16. График переходного процесса по управляющему воздействию при подаче на вход системы х=1 рад и частотой 1 рад/с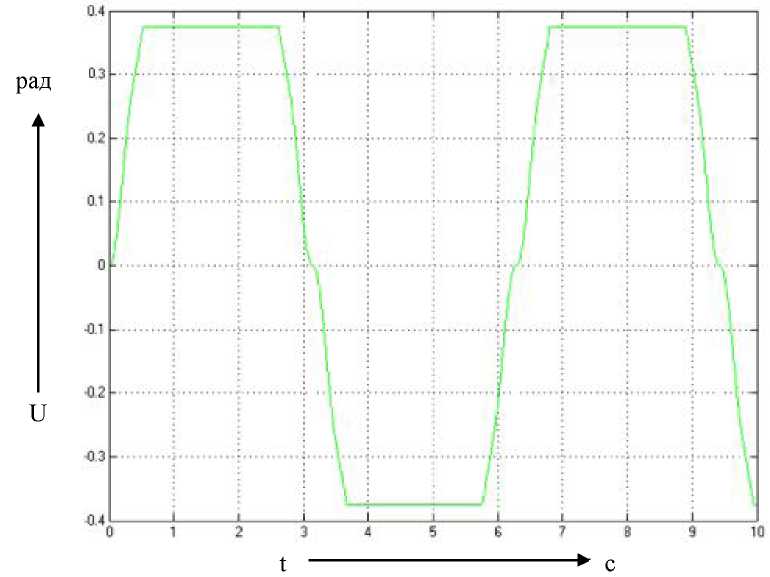

Очевидно, модель не удовлетворяет заданным требованиям качества. Согласно методу повторим пятый этап, увеличив число термов входных и выходных переменных по предлагаемому алгоритму.

Итак, координаты вершин терм-множеств входной переменной по­лученные ранее имеют вид:

-0.5, 0, 0.5

Включим в этот ряд средние арифметические для каждой из пар со­седних элементов:

-0.5, -0.25, -0.125, -0.0625, -0.0313, 0, 0.0313, 0.0625, 0.125, 0.25, 0.5

Аналогично тому, как это было сделано выше, определим термы вы­ходной переменной. Получим:

-0.375, -0.375, -0.375, -0.3344, -0.2837, 0, 0.2837, 0.3344, 0.375, 0.375,

0. 375

Таким образом, термы выходной переменной, представленные на рис. 4.17:

U={bos, sos, mos, n, mps, sps, bps}={-0.375, -0.3344, -0.2837, 0, 0.2837,

0. 3344, 0.375}

Тогда, координатами вершин терм-множеств входной переменной бу­дут:

-0.125, -0.0625, -0.0313, 0, 0.0313, 0.0625, 0.125 имеющие следующие названия x={bos, sos, mos, n, mps, sps, bps }.

Рис. 4.17. Распределение функций принадлежности входного сигнала нечёткого логического регулятора (x - входной сигнал; ц(х) - степень принадлежности

входного сигнала)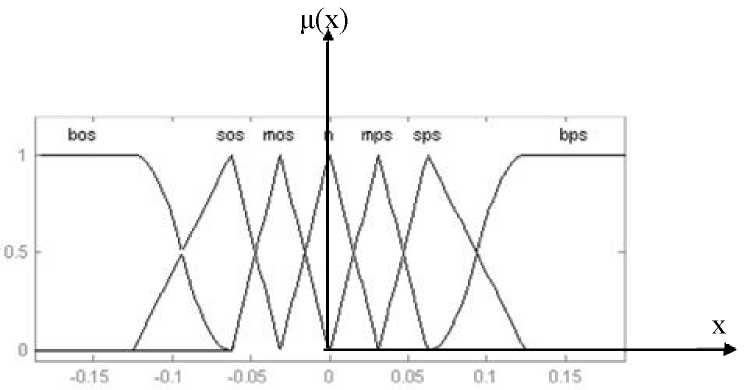

Тогда база правил примет вид:

0. If (х is bos) then (U is bos)

1. If (x is sos) then (U is sos)

2. If (x is mos) then (U is mos)

3. If (х is n) then (U is n)

4. If (x is mps) then (U is mps)

5. If (x is sps) then (U is sps)

6. If (x is bps) then (U is bps)

Оценим адекватность полученной модели. После подачи в систему компенсирующего предупреждающего воздействия среднее квадратичное отклонение составило 0,001393.

Для сравнения полученных результатов было рассчитано классиче­ское последовательное корректирующие устройство, на основе нелиней­ной прямой связи [49] и по методике представленной на рис. 4.10. Тогда на вход нелинейности будет подаваться сигнал смещения, определяемый формулой:

х) = Ь • signx(t) = 0.375 • signx(t).

Среднее квадратичное отклонение в классической системе составило 0,007792, что не удовлетворяет заданным требованиям качества.

Система с нечётким логическим регулятором имеет в 5,6 раза мень­шее среднее квадратичное отклонение. Дальнейшее улучшение регулятора возможно и может быть реализовано при увеличении количества термов входного и управляющего сигналов по предложенному методу.

На рис. 4.18 - 4.20 представлены результаты моделирования систе­мы с нечётким логическим регулятором и классическим нелинейным кор­ректирующим устройством.

2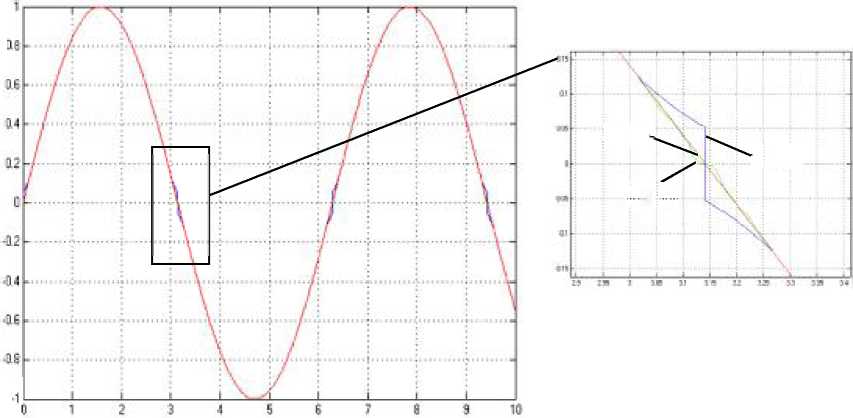

Рис. 4.18. Графики переходных процессов входного и выходного сигналов корректируемой системы при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором; 3 - входной сигнал)

Рис. 4.19. Графики переходных процессов по ошибке при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором)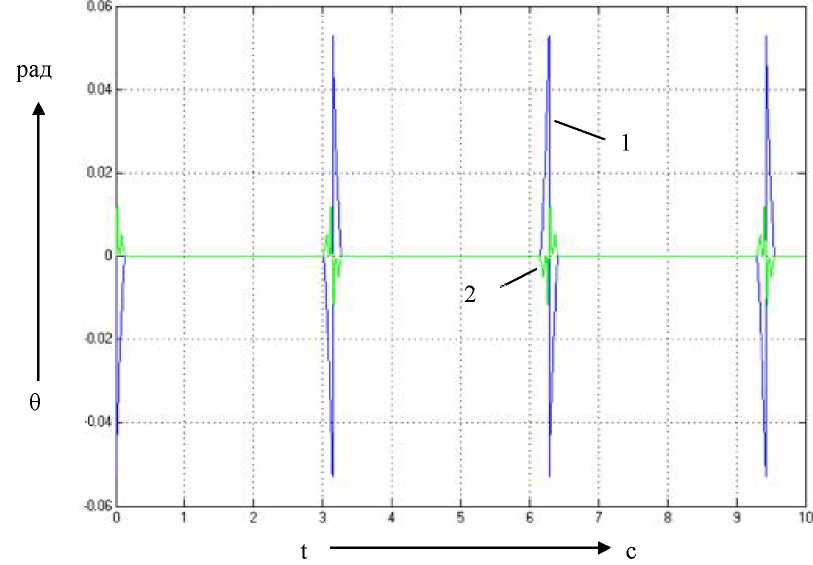

Рис. 4.20. Графики переходных процессов по управляющему воздействию при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором)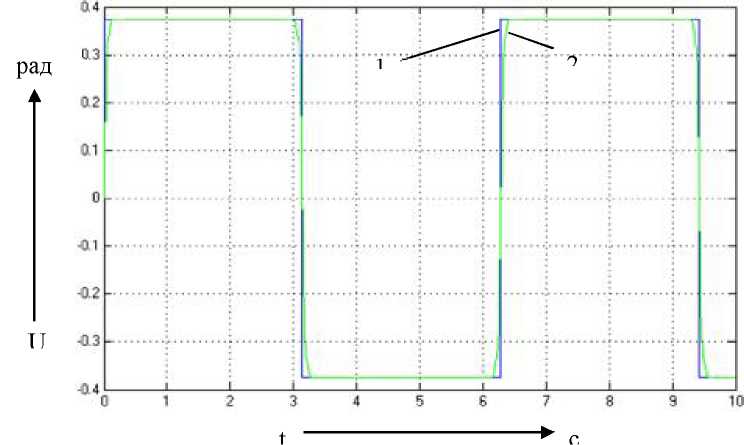

В табл. 4.1 и на рис. 4.21 представлены результаты моделирования системы с нечётким логическим регулятором и классическим нелинейным корректирующим устройством, а также для сравнения системы без ком­пенсирующего воздействия, при изменении половины ширины зоны не­чувствительности (АЬ%). Для каждого значения АЬ%, была получена ошибка (9) и на основании её рассчитано среднее квадратичное отклонение (КМБ(9)), для трех вариантов системы. Строчка в табл. 4.1 со значением АЬ% = 0, соответствует статической характеристике нелинейности пред­ставленной на рис. 4.7. Видно, что система с нечётким логическим регуля­тором на всем исследованном диапазоне (АЬ%= -60...60%) показывает лучшие результаты по сравнению с классическим корректирующим устройством.

Таким образом, нечёткие логические регуляторы, построенные по предлагаемому методу, можно рекомендовать для компенсации нелиней-

ностей при отклонении параметров нелинейности до 30%, при этом обес­печивается допустимая величина ошибки компенсации.

Необходимо отметить, что предлагаемый метод синтеза нечёткого логического компенсатора позволяет использовать его в качестве устрой­ства компенсирующего влияние нелинейности, обеспечивая при этом адаптивность к изменению параметров нелинейности и уровню внешних воздействий. Проведённые исследования подтверждают эффективность предлагаемого метода.

Таблица 4.1

Зависимость среднего квадратичного отклонения (КМ8(0)) в системе от половины ширины зоны нечувствительности (ДЬ%)

дь%, %	Ь, рад	ЛМ8(0), для системы с	ЛМ8(0), для системы с	ЛМ8(0), для системы без
		нечётким логическим	классическим корректиру-	компенсирующего воздей-
		регулятором	ющим устройством	ствия
60	0.8	0.07521	0.0756	0.2966
50	0.75	0.0413	0.04201	0.3142
40	0.7	0.01631	0.01802	0.329
30	0.65	0.002682	0.008122	0.3396
20	0.6	0.008671	0.01157	0.345
10	0.55	0.008306	0.0113	0.3447
0	0.5	0.001393	0.007792	0.3385
-10	0.45	0.01558	0.01749	0.3263
-20	0.4	0.0377	0.03912	0.3082
-30	0.35	0.06586	0.06788	0.2846
-40	0.3	0.09937	0.102	0.2556
-50	0.25	0.1375	0.1406	0.2219
-60	0.2	0.1794	0.183	0.1838

л/>% ► %

Рис. 4.21. Графики зависимости среднего квадратичного отклонения (КМ8(0)) от половины ширины зоны нечувствительности (ДЬ%) при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором; 3 - без компенсирующего воздействия)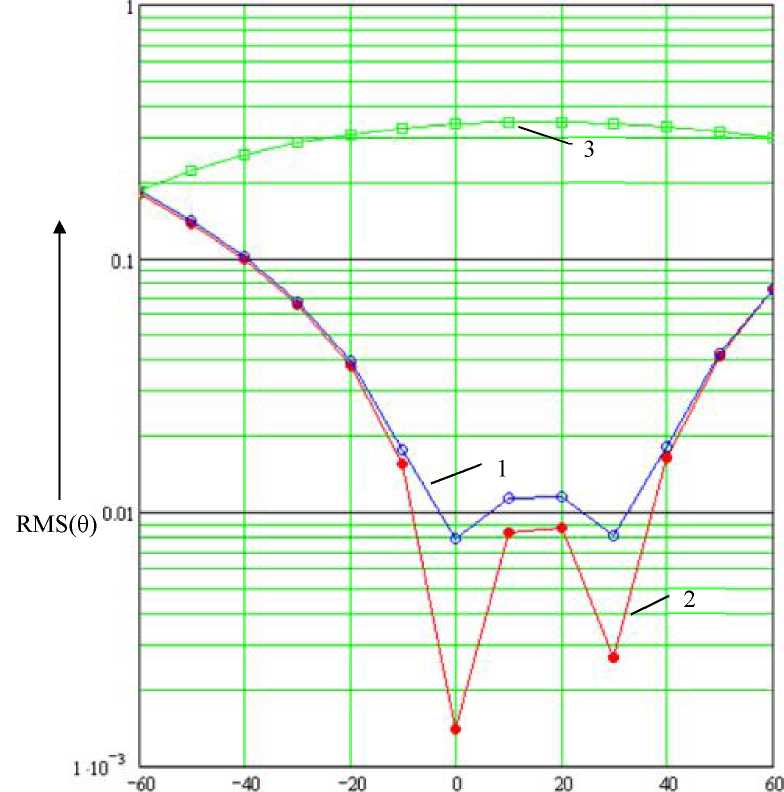

Достоинством метода являются его универсальность и простота ис­пользуемого математического аппарата, а недостатком - ограничение на безынерционность компенсируемых нелинейностей. Таким образом, пред­лагаемый метод применим для коррекции любых безынерционных либо малоинерционных систем автоматического управления. Для ослабления вышеотмеченного недостатка можно предложить несколько иной способ компенсации естественных нелинейностей, что показано в следующем разделе.

2. Способ компенсации естественных нелинейностей с использованием ошибки компенсации

Как и в ранее рассмотренном методе предлагается для компенсации нелинейных свойств объектов регулирования использовать аппарат нечёт­кой логики [8, 49]. При этом ограничения, накладываемые на нелинейный элемент и указанные выше, сохраняются. Тогда можно предложить способ синтеза нечёткого логического регулятора с использованием ошибки ком­пенсации, включающий в себя следующие этапы [57, 64, 65]:

1. Формулировка задач компенсации и определение требований к ка­честву;

2. Определение вида компенсируемой нелинейности (однозначная, неоднозначная). Определение возможных вариантов компенсации (спосо­бов подачи компенсирующего воздействия);

3. Выбор оптимального варианта компенсации;

4. Построение модели нечёткого логического регулятора (фаззифи- кации входных переменных, дефаззификации выходной и формирования базы нечётких правил);

5. Проверка адекватности полученной модели;

6. Техническая реализация нечёткого логического регулятора на ос­нове полученной модели.

На первом этапе, как и ранее, согласно предлагаемому способу необ­ходимо сформулировать задачу компенсации исследуемой системы (нели­нейного элемента) и определить требования к качеству этой компенсации.

На втором этапе, исходя из требований, полученных на предыдущем этапе, необходимо определить способ подачи в исследуемую систему ком­пенсирующего воздействия.

Рис. 4.22. Структурная схема компенсации введением компенсирующей связи с нечётким логическим регулятором с подачей сигнала коррекции на вход нелинейности (memory - блок задержки на один расчётный шаг; т - время

задержки)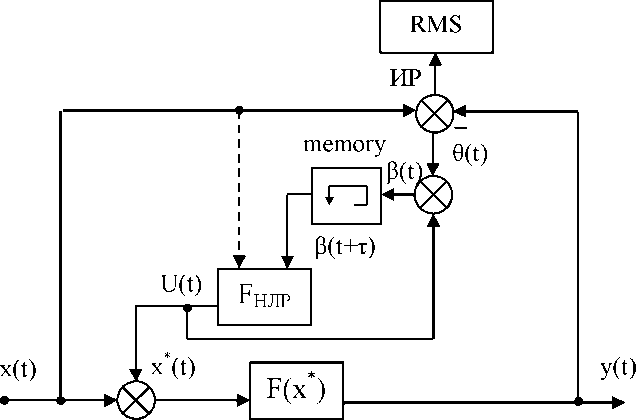

Структурно включение компенсирующего устройства (нечёткого ло­гического регулятора на рис.1.16) можно реализовать по двум вариантам:

1. введение компенсирующей связи с нечётким логическим регуля­тором с подачей сигнала коррекции на вход нелинейности (рис. 4.22);

2. введение компенсирующей связи с нечётким логическим регуля­тором с подачей сигнала коррекции на выход нелинейности (рис. 4.23).

В соответствии с рисунком имеем:

' X *^(t) = X^(t) + Р_Шр,

< ^{b (}t⁾ = в ⁽t⁾ + F_mp,

. У^(t) = ^{F (X}*⁾.

Рис. 4.23. Структурная схема компенсации введением компенсирующей связи с нечётким логическим регулятором с подачей сигнала коррекции на выход нелинейности (memory - блок задержки на один расчётный шаг; т - время

задержки)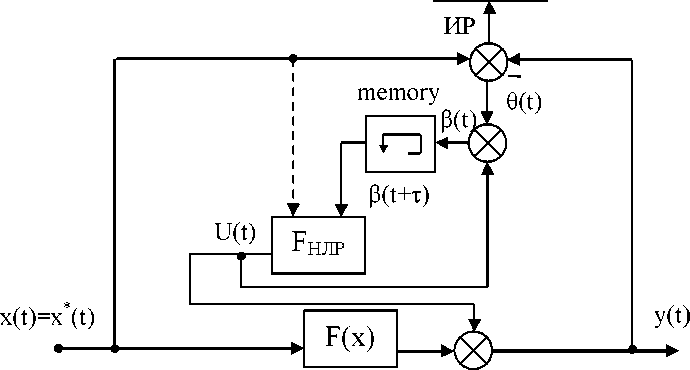

Тогда:

^(t) = ^{q (}t⁾ + F_HJ1P,

IУ ^(t) = ^{F (x)} + ^Fhjp •

Необходимо отметить, что применение блока memory в выше пред­ставленных схемах необязательно и возможно использование аналогов, например транспортное запаздывание (на время т).

Для приведённых вариантов схемных решений, как и в предыдущем методе, не указаны аргументы нечёткой логической функции F_HJP и соот­ветственно не показы входные сигналы нечёткого логического регулятора. Выбор конкретных анализируемых сигналов для реализации наиболее эф­фективной компенсации является отдельной задачей, решение которой за­висит от вида нелинейности и технических требований к реализации. Ре­комендуемыми сигналами для анализа в случае однозначной нелинейности являются входной сигнал x(t) и сигнал fi(t+r). Для неоднозначных нелиней­ностей вместо входного сигнала x(t) следует рассматривать производную этого сигнала по времени dx(t)/dt.

На третьем этапе производится выбор оптимального варианта схемы компенсации. Предпочтительными являются первый вариант, так как в случае, если нелинейностью обладает исполнительный орган, реализация второго варианта компенсации не только представляет существенные тех­нические трудности, но и зачастую является невыполнимой. Второй вари­ант схемы можно также рекомендовать для компенсации нелинейностей типа «насыщение», компенсация которых по первому варианту невозмож­на.

На четвёртом этапе производится построение модели нечёткого ло­гического регулятора на основе результатов, полученных на предыдущих этапах. Для построения модели нечёткого логического регулятора (фаззи- фикации входных переменных, дефаззификации выходной и формирова­ния базы нечётких правил) предлагается использовать следующий алго­ритм.

1. Формируется распределения термов входного сигнала.

Для обоих вариантов схемных решений распределение входных тер­мов нечёткого логического регулятора (входной сигнал х^), сигнал в^+т) для однозначной нелинейности и производная входного сигнала по време­ни йХ(?)/^? сигнал в^+т) для неоднозначной нелинейности) одинаково.

При идентификации каждого входного сигнала нечёткого логическо­го регулятора предлагается использовать три функции принадлежности. Такое количество предоставляет возможность однозначного определения нахождения каждого из входных сигналов регулятора в положительной, отрицательной или нулевой области.

Диапазон распределения функций принадлежности для первого вхо­да (сигнал в(^+т)) должен быть не меньше предполагаемой ширины зоны нечувствительности, люфта и т.д., а для второго - предельных значений входного сигнала (при компенсации однозначной нелинейности) или его

производной (при компенсации неоднозначной нелинейности). Для ком-

134

пенсации динамических нелинейностей следует выбирать более широкий, симметричный относительно нуля диапазон распределения функций при­надлежности первого входа.

Таким образом, для крайних терм-множеств следует выбрать 2- и £- образный вид, для центрального - треугольный (рис. 4.24).

Терм-множества входных переменных, имеют следующие названия:

х={об, п, рб) - входной сигнал,

dx/dt={oБ, п, рб) - производная входного сигнала,

в={оБ, п, рб) - сигнал в^+т),

означающие соответственно: об - «отрицательный сигнал», п - «нулевой сигнал», рБ - «положительный сигнал».

Рис. 4.24. Распределение функций принадлежности входных сигналов нечёткого логического регулятора (х - входной сигнал; dxldt - производная входного сигнала; в - сигнал Д^+т); ц(х) - степень принадлежности входного сигнала; |x(dxldt) - степень принадлежности производной входного сигнала; ц(в) - степень

принадлежности сигнала в(7+т))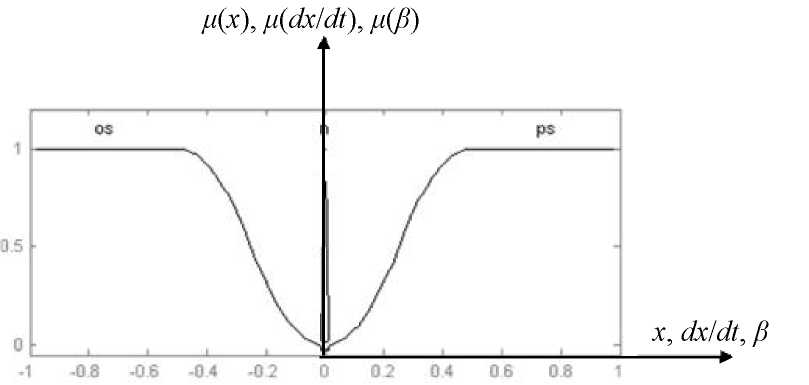

2. Способ определения термов выходной переменной не зависит от выбранной ранее схемы реализации.

В качестве выходного сигнала используется сигнал, линейный отно­сительно первого (сигнал в^+г)) входного сигнала с коэффициентом про­порциональности, равным 1, -1 или 0.

В зависимости от используемого алгоритма нечёткого вывода способ задания термов может отличаться.

В случае использования, например, алгоритма Сугено задаются ко­эффициенты при входной переменной в равные соответственно 1, -1 или 0. При построении модели нечёткого логического регулятора по алгоритму Мамдани определяют синглтоны.

Тогда, выходная лингвистическая переменная и={оБ, п, рб) имеет три функции принадлежности об, рб и п, описывающие эти линейные зави­симости:

об и - [0 -1 0]

п и - [0 0 0] (3)

рБ и - [0 1 0]

5. При построении базы нечётких правил (знаний) для каждого терма входных переменных, соответствующему входному сигналу (его произ­водной), сигналу Р(1+т), и терму выходной переменной строится правило нечёткой продукции.

Тогда, в случае компенсации однозначной (неоднозначной) нелинейно­сти:

1. 1И (х (йх/йР) 1б об) апё (в 1Б об) Шеп (и 1б рб)

2. 1И (х (йх/йР) 1б об) апё (в 1Б рб) Шеп (и 1б об)

3. 1И (х (йх/йР) 1б рб) апё (в 1Б об) Шеп (и 1б об) (4)

4. 1И (х (йх/йР) 1б рб) апё (в 1Б рб) Шеп (и 1б рб)

5. 1И (х (в 1б п) ог (в 1б п) Шеп (и 1б п)

В качестве метода агрегирования, как и ранее, следует использовать операцию тах - максимум. На нечёткую импликацию ограничений не накладывается; например, её можно проводить с использованием метода min - минимум. Дефаззификацию рекомендуется проводить методом цен­тра тяжести (взвешенное среднее).

На пятом этапе проводится проверка адекватности полученной мо­дели. Для более качественной проверки следует подавать на вход модели синусоидальный сигнал с амплитудой не меньше максимальной прогнози­руемой в процессе эксплуатации корректируемой системы. Желательно исследовать поведение модели на некотором интервале вероятных ампли­туд входного сигнала и оценить среднее квадратичное отклонение выход­ного сигнала корректируемой системы от требуемого. Если качество ком­пенсации нелинейности системы неудовлетворительное, следует умень­шить время задержки т. Но с другой стороны т связано с расчётным шагом At, должно выполняться условие: т > At. То есть уменьшение времени за­держки приведёт к уменьшению расчётного шага, что в свою очередь по­влияет на скорость вычислений и быстродействие нечёткого логического регулятора.

На шестом этапе осуществляется техническая реализация нечёткого логического регулятора. При выборе аппаратной базы, как и в первом ме­тоде, следует, прежде всего, руководствоваться соображениями экономич­ности, т.к. модель, построенная по предлагаемому алгоритму, может быть реализована практически на любой аппаратной базе с общепромышленным управляемым контроллером.

Так как в предложенном нечётком логическом регуляторе в качестве в качестве одного из входных сигналов используется сигнал ß(t+f)=e(f)+U(t), т.е. регулятор отслеживает изменение ошибки компенса­ции 6(t) и пытается её минимизировать, поэтому будет обеспечиваться не­прерывный контроль качества процесса компенсации, и осуществляться автоматическая подстройка нечёткого логического регулятора при измене­нии параметров корректируемой системы или уровня внешних воздей­ствий, т.е. регулятор изначально обладает адаптивными свойствами.

2. Проверка эффективности предлагаемого способа на примере компенсации нелинейности с использованием ошибки компенсации

Проверка эффективности предлагаемого способа была осуществлена в среде инженерных вычислений Matlab пакет Simulink и Fuzzy Logic [8, 43]. Воспользуемся моделью нелинейного элемента, имеющего статиче­скую характеристику представленную на рис. 4.7.

Структурная схема элементарной нелинейной системы, содержащей данный элемент, представлена на рис. 4.8, где F(x) - некоторая априорно аналитически не определённая функция, описывающая нелинейный эле­мент со статической характеристикой, изображённой на рис. 4.7.

Проведём поэтапный синтез нечёткого логического регулятора для компенсации данной нелинейности по предлагаемому способу.

Первый этап. Пусть требуется компенсировать нелинейность (см. рис. 4.8) системы. При этом среднее квадратичное отклонение выходного сигнала системы y(t) от входного x(t) не должно превышать 0,0025.

Второй этап. В данном случае возможно реализовать любой из рас­сматриваемых вариантов подачи компенсирующего воздействия.

Третий этап. В качестве оптимального выберем первый вариант ком­пенсации. Так как каждому значению входного сигнала соответствует только одно значение выходного, статическая характеристика однозначна. Следовательно, в качестве входных сигналов нечёткого логического регу­лятора будем использовать входной сигнал x(t) и сигнал y0(t+r). Тогда схема скомпенсированной системы будет иметь вид представленный на рис. 4.22.

Четвёртый этап. Проведём построение модели нечёткого логическо­го регулятора (рис. 4.25) по предлагаемому алгоритму.

1. Распределение термов входного сигнала x(t) и сигнала y0(t+r) пред­ставлено на рис. 4.24.

2. Термы выходной переменной показаны в (3).

3. База правил необходимая для выработки управляющих сигналов представлена в (4).

В качестве алгоритма нечёткого логического вывода, например, применим Сугено первого порядка. Согласно предлагаемому способу агре­гирование производиться операцией max - максимум, в качестве нечёткой импликации использовался метод min - минимум. Для дефаззификации применим метод wtaver - взвешенное среднее.

Рис. 4.25. Функциональная схема нечёткого логического регулятора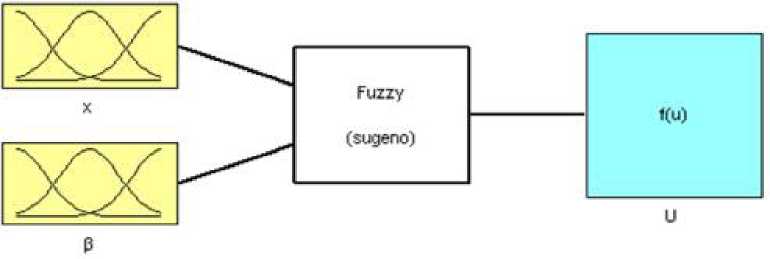

Пятый этап. Для оценки адекватности полученной модели был про­ведён анализ графиков входного и выходного сигналов корректируемой системы до и после подачи компенсирующего воздействия. Как и в преды­дущем методе на вход нелинейного элемента был подан синусоидальный сигнал (х=1 рад, т=1 рад/с). В нескорректированной системе (см. рис. 4.8) среднеквадратичное отклонение выходной величины от входной было рав­но 0,3385. После подачи в систему компенсирующего воздействия (см. рис. 4.22) среднее квадратичное отклонение составило 0,002376.

Для сравнения полученных результатов воспользуемся классическим последовательным корректирующим устройством, на основе нелинейной прямой связи рассчитанным ранее.

Среднее квадратичное отклонение в классической системе составило 0,007792, что не удовлетворяет заданным требованиям качества.

Полученная система с нечётким логическим регулятором имеет в

3. раза меньшее среднее квадратичное отклонение. Дальнейшее улучшение регулятора возможно и может быть реализовано при уменьшении времени задержки т.

На рис. 4.26 - 4.28 представлены результаты моделирования системы с нечётким логическим регулятором и классическим нелинейным коррек­тирующим устройством.

рад

1

3

2

У,

Рис. 4.26. Графики переходных процессов входного и выходного сигналов корректируемой системы при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором; 3 - входной сигнал)

Рис. 4.27. Графики переходных процессов по ошибке при подаче на вход системы х=1 рад. и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором)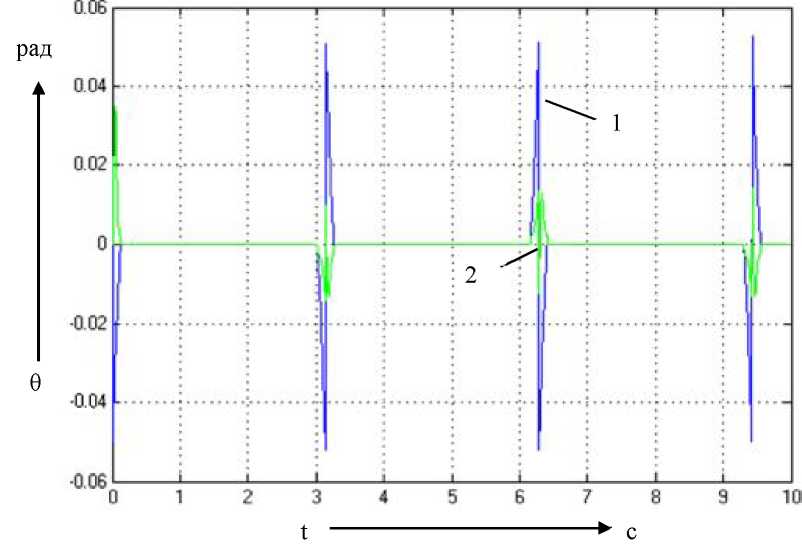

Рис. 4.28. Графики переходных процессов по управляющему воздействию при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором)

141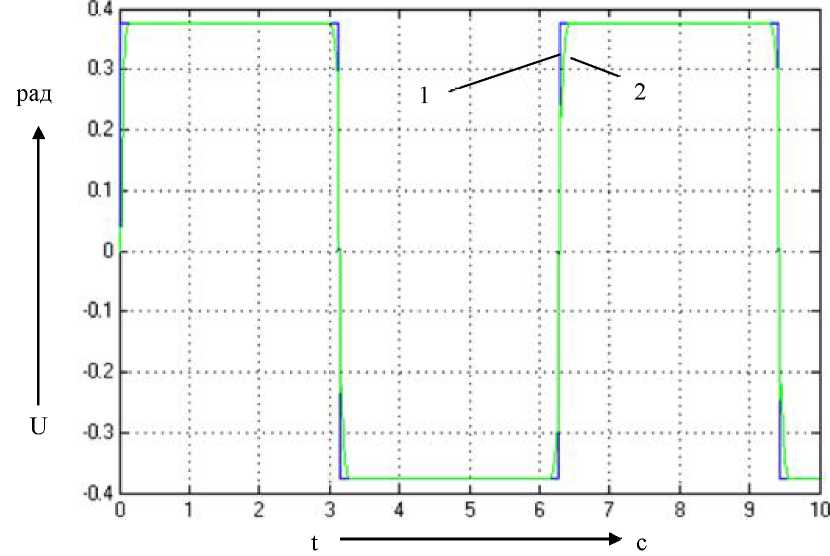

В табл. 4.2 и на рис. 4.29 представлены результаты моделирования системы с нечётким логическим регулятором и классическим нелинейным корректирующим устройством, а также для сравнения системы без ком­пенсирующего воздействия, при изменении половины ширины зоны не­чувствительности (АЬ%). Для каждого значения АЬ%, была получена ошибка (9) и на основании её рассчитано среднее квадратичное отклонение (КМБ(9)), для трех вариантов системы. Строчка в табл. 4.2 со значением АЬ%=0, соответствует статической характеристике нелинейности пред­ставленной на рис. 4.7.

Таблица 2.2

Зависимость среднего квадратичного отклонения (ЯМ8(9)) в системе от половины ширины зоны нечувствительности (ДЬ%)

дь%, %	Ь, рад	КМБ(9), для системы с	КМБ(9), для системы с	ЛМ8(0), для системы без
		нечётким логическим	классическим корректиру-	компенсирующего воздей-
		регулятором	ющим устройством	ствия
100	1	0.003535	0.4808	0.25
90	0.95	0.003435	0.2296	0.2527
80	0.9	0.003235	0.1696	0.2627
70	0.85	0.003035	0.1182	0.2784
60	0.8	0.002739	0.0756	0.2966
50	0.75	0.002555	0.04201	0.3142
40	0.7	0.002449	0.01802	0.329
30	0.65	0.002403	0.008122	0.3396
20	0.6	0.002392	0.01157	0.345
10	0.55	0.002391	0.0113	0.3447
0	0.5	0.002376	0.007792	0.3385
-10	0.45	0.002324	0.01749	0.3263
-20	0.4	0.0022	0.03912	0.3082
-30	0.35	0.001942	0.06788	0.2846
-40	0.3	0.001516	0.102	0.2556
-50	0.25	0.0009775	0.1406	0.2219
-60	0.2	0.0004675	0.183	0.1838
-70	0.15	0.0001405	0.2284	0.1419
-80	0.1	4.13510-5	0.276	0.09688
-90	0.05	1.911-10°	0.3251	0.04934
-100	0	0	0.375	0

Разработанный способ синтеза нечёткого логического регулятора позволяет использовать его в качестве устройства компенсирующего влия­ние нелинейности, обеспечивая при этом хорошую адаптивность к измене­нию параметров нелинейности и уровню внешних воздействий, по сравне­нию с компенсацией нелинейности по статической характеристике и клас­сическим нелинейным корректирующим устройством. Проведённые ис­следования подтверждают эффективность предлагаемого способа.

Достоинством способа являются его универсальность и простота ис­пользуемого математического аппарата, а недостатком, как и в первом ме­тоде - ограничение на безынерционность компенсируемых нелинейностей. Таким образом, предложенный способ применим для коррекции любых безынерционных либо малоинерционных систем автоматического управ­ления.

Т.е., нечёткие логические регуляторы, построенные по предлагаемому способу, можно рекомендовать для компенсации нелинейностей при откло­нении параметров до 100% и более, при этом обеспечивается допустимая ве­личина ошибки компенсации. Однако необходимо отметить, что первый ме­тод компенсации нелинейности по статической характеристике показал луч- тттие результаты при настройке на заданную нелинейность (ДЬ%=0) и в обла­сти малых изменений параметров нелинейности табл. 4.1, 4.2, рис. 4.21, 4.29. При этом расчётный шаг в обоих случаях был одинаков и составлял Д?=0,005 с. В табл. 4.3 и на рис. 4.30 представлены результаты моделирова­ния системы с нечётким логическим регулятором при использовании ошибки компенсации, при изменении расчётного шага (Д1%о). Для каждого значения Д1%, была получена ошибка (в) и на основании её рассчитано среднее квад­ратичное отклонение (КМБ(в)).

—
	п п— 5	>_а о ,	/
		3
	>и
г	\
	. V	-- 1
1
, с-100,0)
			2
			/
		и» *
	К*
	—
-/	—
Т
/
/
7
г
/
Д 100,0)

0.01

-100 '50 0 50 100

Л/>% ► %

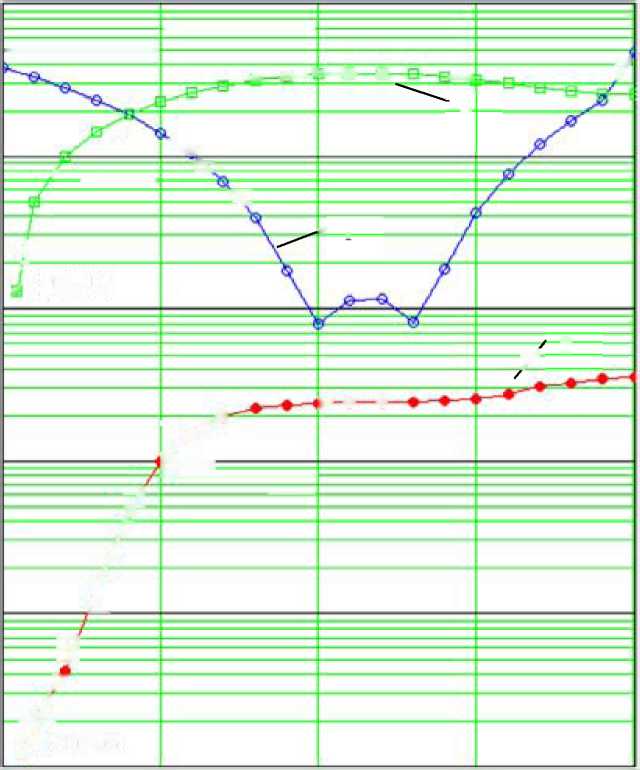Рис. 4.29. Графики зависимости среднего квадратичного отклонения (КМ8(0)) от половины ширины зоны нечувствительности (ДЬ%) при подаче на вход системы х=1 рад и частотой 1 рад/с (1 - классическое корректирующие устройство; 2 - с нечётким логическим регулятором; 3 - без компенсирующего воздействия)

Рис. 4.30. График зависимости среднего квадратичного отклонения (КМ8(0)) от расчётного шага (Д/%) при подаче на вход системы х=1 рад и частотой 1 рад/с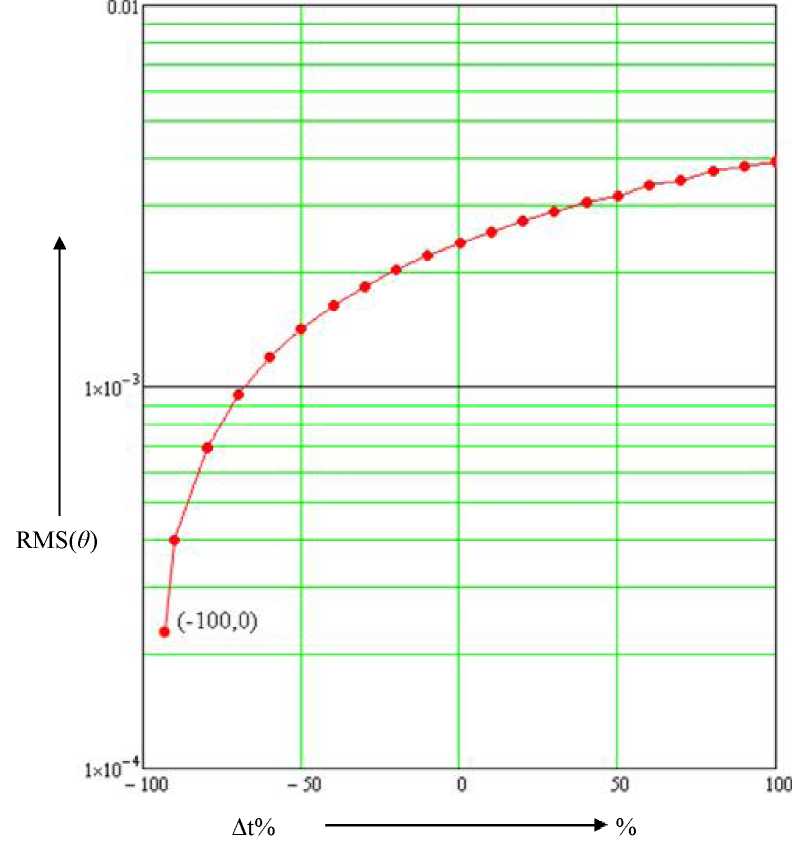

Строчка в табл. 4.3 со значением Д/%=0, соответствует статической характеристике нелинейности представленной на рис. 4.7. На рис. 4.30 не представлены графики зависимости для классического компенсирующего устройства и нечёткого логического регулятора построенного с примене­нием статической характеристики нелинейности, так как в области стан­дартного инженерного расчётного шага (соизмеримого с временем пере­ходного процесса) наблюдается инвариантность.

расчётного шага (А?%)

Таблица 4.3

Зависимость среднего квадратичного отклонения (КМ8(0)) в системе от

А%, %	А, с	КМБ(0), для системы с нечётким логическим регулятором
100	0.01	0.003901
90	0.0095	0.003798
80	0.009	0.003688
70	0.0085	0.003487
60	0.008	0.003364
50	0.0075	0.003173
40	0.007	0.003034
30	0.0065	0.002869
20	0.006	0.002725
10	0.0055	0.002553
0	0.005	0.002376
-10	0.0045	0.002213
-20	0.004	0.002025
-30	0.0035	0.001833
-40	0.003	0.001631
-50	0.0025	0.00142
-60	0.002	0.001196
-70	0.0015	0.0009567
-80	0.001	0.0006943
-90	0.0005	0.0003969
-100	^0	0

Таким образом, первый метод компенсации нелинейности по стати­ческой характеристике в идеальном случае можно рекомендовать для не­линейных объектов с незначительно изменяющимися параметрами и в си­стемах, где требуется достаточно высокий уровень быстродействия.

Способ компенсации нелинейности с использованием ошибки ком­пенсации следует использовать для нелинейных объектов параметры, ко­торых изменяться во времени и связаны с конструктивными особенностя­ми. Кроме того, плавность и быстрота настройки нечёткого логического регулятора на параметры нелинейности, позволяет использовать данный

способ не только для коррекции систем, обладающих нелинейностью

146

вследствие износа механизмов или особенности конструкции, но и реко­мендовать его внедрение на стадии проектирования изделий, содержащих узлы, подверженные риску возникновения нелинейности в процессе экс­плуатации, с целью увеличения срока службы и эффективности работы та­ких изделий.

Таким образом, изложенная выше методика компенсации естествен­ных сопутствующих однозначных и неоднозначных нелинейностей с ис­пользованием мягких вычислений, позволяет улучшить качество переход­ных процессов в системах автоматического управления. При этом показа­тели качества переходных процессов на уровне аналогичных при исполь­зовании классических методов компенсации. Кроме того, следует отметить что используемый авторами метод оптимизации распределения функций принадлежности и безэкспертного проектирования базы знаний нечёткого логического компенсатора, позволяет сократить затраты на статистические опросы экспертов и исключить человеческий фактор из процесса её настройки. Использование комбинации видов функций принадлежности позволяет существенно упростить модель нечёткого логического компен­сатора и его техническую реализацию.