Глава 3. Классические методы синтеза систем управления с нечёткой информацией

В соответствии с существующей классификацией интеллектуализи- рованных СУ технологическими процессами, проектирование и исследо­вание таких систем проводится с двух позиций - структурной и алгорит­мической.

На структурном уровне анализируется целесообразность использо­вания НЛР в том или ином тракте управления в зависимости от того, где и как проявляется неопределённость. При этом анализу подлежит способ ре­ализации нечёткого управления:

• нечёткое управление по дополнительному каналу управления;

• непосредственное нечёткое управление по основному каналу управления;

• комбинированное нечёткое управление.

На алгоритмическом уровне анализируется эффективность и целе­сообразность использования конкретного метода нечёткого вывода, а именно:

• алгоритма Мамдани;

• алгоритма Сугено;

• гибридного алгоритма.

1. Нечёткое управление по дополнительному каналу

Для повышения динамической точности систем управления энерге­тическими процессами часто используют принцип динамической коррек­ции, заключающийся в том, что в системе, наряду с традиционным регуля­тором, используют дополнительный корректирующий тракт [2, 38, 60]. При этом в задачу дополнительного корректирующего тракта входит вы­работка вспомогательного управляющего воздействия, совместное дей­ствие которого с корректирующим сигналом основного регулятора обес­печивает требуемое качество динамических характеристик объекта регу­лирования. Однако такой принцип коррекции эффективен при условии ли­нейности и неизменности параметров системы управления. В противном случае реализацию дополнительного тракта коррекции целесообразно пе­ревести в область нечёткого управления. Поскольку основной контур ре­гулирования представляет собой детализированную структуру, то при син­тезе алгоритма управления нечётким корректирующим трактом желатель­но использовать известные из теории управления методы. В качестве по­следних могут быть использованы: метод параллельной коррекции (на ос­нове желаемой передаточной функции параллельного корректирующего звена определяются основные параметры нечёткого корректора, а затем с помощью итерационного моделирования его алгоритм изменяется в сторо­ну достижения желаемого качества регулирования), методы оптимального управления (на основе выбранного интеграла качества для детализирован­ной структуры системы определяется требуемый вид управляющего воз­действия, из него выделяется составляющая не реализуемая традиционным регулятором, по которой и находятся основные параметры нечёткого кор­ректора) [33].

Отсюда задача синтеза нечёткого корректора переходит в область логических заключений и сводится:

• выбору входных лингвистических переменных на основе анализа поведения замкнутой детализированной системы в оптимальном режиме;

• назначению для каждой из лингвистических переменных набора термов;

• выбору для каждого из термов аппроксимирующего нечёткого множества;

• созданию базы правил корректора на основе анализа совокупности значений «входные переменные - управление», полученной для оптималь­ного режима;

• принятию адекватного механизма нечёткого вывода и выбору эф­фективного метода преобразования полученного нечёткого управления в «чёткий» выходной сигнал.

Более подробно приведённый алгоритм синтеза нечёткого канала коррекции рассмотрим на примере системы регулирования температуры перегретого пара [10, 30, 35].

Кратко охарактеризуем объект регулирования. Температура пара на выходе парогенератора относится к важнейшим параметрам, определяю­щим экономичность работы паровой турбины и энергоблока в целом.

Анализируемая СУ предназначена для стабилизации заданного температурного режима в паровом тракте котла за счёт регулирования впрыска собственного конденсата.

Паровой котёл современной электростанции имеет развитый паро­перегреватель, состоящий из нескольких ступеней, отличающихся друг от друга расположением, протяжённостью и способом обогрева. От способа обогрева зависит характер основного возмущающего воздействия, дей­ствующего на данную ступень. Каждая ступень имеет свою собственную локальную систему регулирования температуры перегретого пара, при­званную держать в заданном соотношении температуру пара на выходе из данной ступени. Возмущение, повлёкшее за собой отклонение температу­ры в одной ступени, последовательно отражается и на температуре в по­следующих ступенях пароперегревателя.

На температуру пара оказывает влияние большое количество фак­торов (нагрузка котла, шлакование топки, загрязнение поверхностей

61

нагрева, температура питательной воды, избытки воздуха, помол топлива и т.д.), часть из которых трудно или практически невозможно оценить коли­чественно.

1. Модель объекта управления

Для барабанных парогенераторов наиболее распространён способ регулирования температуры первичного пара при помощи пароохладите­лей [45]. Современные котлоагрегаты оснащаются впрыскивающими па­роохладителями. Принцип их действия основан на изменении энтальпии частично перегретого пара за счёт тепла, отбираемого на испарение охла­ждающей воды, впрыскиваемой в паропровод.

Конструктивно участок регулирования перегрева образует часть поверхности нагрева пароперегревателя, включая обогреваемые и необо­греваемые трубы, от места ввода охлаждающего агента до выходного кол­лектора, в котором необходимо поддержать заданную температуру.

Принципиальная схема существующей [46] автоматизированной СУ температуры перегрева первичного пара представлена на рис. 3.1.

Регулятор перегрева получает основной сигнал отклонения темпе­ратуры пара на выходе пароперегревателя П и дополнительный - пропор­циональный производной от температуры на выходе при изменениях эн­тальпии частично перегретого пара 1_пр и исчезающий при Ж_пр/Ж=0.

К возмущающим воздействиям относятся энтальпия на входе в уча­сток 1_вх, расход потребляемого пара Б_пп и количество тепла Q _т, восприни­маемое от топочных газов. Выходной величиной участка является энталь­пия на выходе из пароперегревателя 1₀. Регулирующим воздействием явля­ется расход охлаждения О_тр.

Динамические характеристики пароперегревателя неодинаковы по каналам возмущающего и регулирующего воздействий, но обладают об­щим свойством - значительной инерционностью.

Пароперегреватель является объектом регулирования с распреде­лёнными параметрами и описывается дифференциальными уравнениями нестационарного теплообмена. Для описания его динамики принимают ряд упрощающих предположений [28], а именно: плотность, давление, тепло­ёмкость пара и коэффициент теплоотдачи постоянны по всей длине паро­перегревателя; изменение расхода пара приводит к изменению коэффици­ента теплоотдачи; в радиальном направлении стенки трубопроводов абсо­лютно теплопроводны; продольные тепловые потоки, связанные с тепло­проводностью в паре и металле, не учитываются.

Рис. 3.1. Принципиальная схема существующей автоматизированной СУ температуры перегрева первичного пара (1 - барабан; 2, 3 - ступени пароперегревателя; 4 - пароохладитель; 5 - регулирующий клапан впрыска; 6 - охладитель пара; 7 - сборник конденсата; 8 - гидрозатвор; 9 - дифференциатор; 10 - регулятор)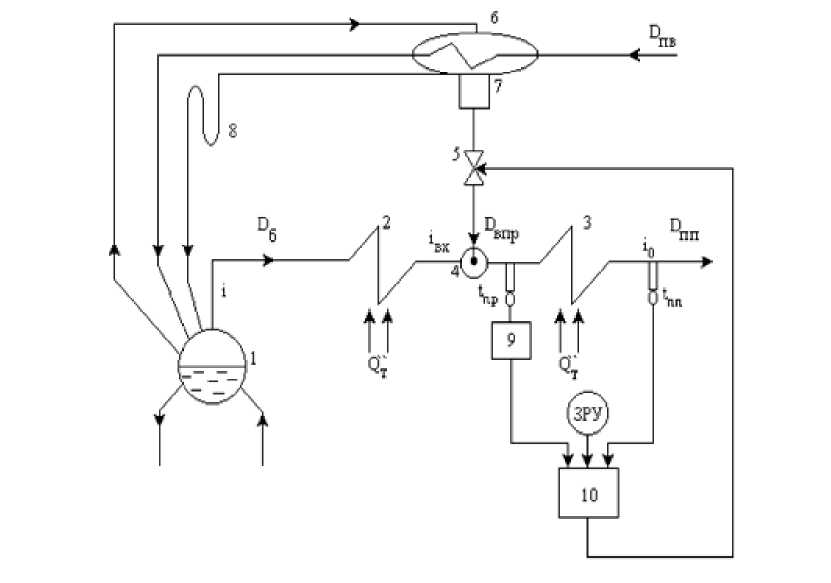

В [28] динамическая модель типовой автоматизированной СУ тем­пературы перегретого пара реализована в виде звеньев структурной схемы,

передаточные функции которых получены экспериментальным путём (рис.3.2).

Для данной модели:

Жоп (р)

к

оп

^Топ^р + ¹ ’

- №_оп(р) - передаточная функция участка трубопровода от места впрыска до места установки датчика температуры ґ_пр (передаточная функ­ция опережающего участка, включая датчик і_пр):

где К_оп - коэффициент усиления передаточной функции опережающего участка, °С/(т/ч); Т_оп - постоянная времени передаточной функции опере­жающего участка, с.

^(Тин р + ¹⁾

Ж„н (р) =

к

ин

е

-рт

- №_ин(р) - передаточная функция пароперегревателя между местами установки датчиков температуры ґ_пр и ї_пп, (передаточная функция инерци­онного участка, включая датчик і_пп):

Рис. 3.2. Структурная схема типовой АСР температуры

перегрева пара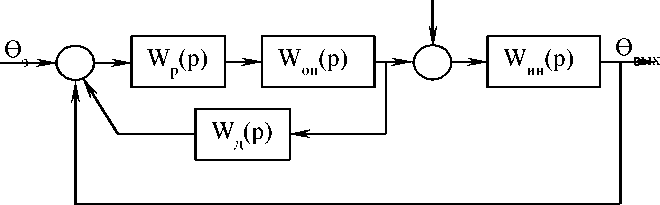

где К_ин - коэффициент передачи инерционного участка, °С/(т/ч); Т_ин - по­стоянная времени передаточной функции инерционного участка, с; т - время запаздывания.

- Ж_д(р) - передаточная функция дифференциатора представляющая собой реальное дифференцирующее звено и служащая для упреждающей коррекции изменения температуры пара на выходе:

К _д Р

Т_д Р +1’

где К_д - коэффициент усиления, зависящий от аппаратной реализации дифференциатора и измерительного блока; Т_д - постоянная времени диф­ференциатора, определяемая ручной подстройкой в режиме наладки.

- Ж_р(р) - передаточная функция регулятора, который управляет по­ложением регулирующего клапана и реализует ПИ-закон регулирования, обеспечивающий исключение статической ошибки регулирования:

кр (р) =

К р (Тр р+1)

Тр Р

где К_р - коэффициент усиления регулятора,°С/(т/ч); Т_р - постоянная вре­мени регулятора, с.

- д₃,, 0_вых, в_возм - задание температуры на выходе пароперегревателя, реальная температура на выходе перегревателя и возмущение соответ­ственно. Причём все виды возмущающих воздействий, отмеченных ранее, представлены в виде эквивалентного значения в_во3м, которое может быть как положительным, так и отрицательным. Положительное значение воз­мущающего воздействия в_во3м будет говорить о повышении тепловосприя­тия радиационными и конвективными поверхностями нагрева паропере­гревателя или уменьшении расхода пара, и наоборот.

Следует отметить, что в дальнейшем рассматривается только режим стабилизации температуры перегретого пара, который можно отнести к режиму работы в «малом». Пуск системы, с поднятием температуры до за­данной, осуществляется по принципу поэтапного повышения температуры

в_вых и не может быть исследован с помощью приведённой структурной схемы.

Основным недостатком приведённой системы стабилизации являет­ся сравнительно невысокая динамическая точность при действии недетер­минированных возмущений. Для повышения динамической точности в [10, 33] предлагается ввести в систему регулирования дополнительную коррекцию управляющего сигнала. Для этого сигнал ошибки регулирова­ния дополнительно дифференцируют, затем полученное значение пере­множают непосредственно с сигналом ошибки и вычисленное значение интегрируют. Проинтегрированное значение суммируют с сигналом ошиб­ки, используя его в качестве корректирующего. Однако такой подход не обеспечивает достижения желаемого результата, в силу того, что парамет­ры динамических звеньев структурной схемы в реальной системе не по­стоянны из-за учёта их физических особенностей (см. принимаемые допу­щения при математическом описании).

Поэтому более целесообразно использовать коррекцию стандартно­го регулятора в нечётком виде, как предложено в [39, 56].

Рассмотрим последовательно этапы синтеза нечёткого корректора, учитывая при этом, что коррекция динамической ошибки переносится из аппаратной области в информационно-программную.

2. Синтез нечёткого регулятора

Поскольку на нечёткое корректирующее звено возлагается задача выработки упреждающего корректирующего воздействия в диапазоне изменения динамической ошибки системы стабилизации, при синтезе нечёткого регулятора используем алгоритм вывода по Мамдани, как наиболее простой и интуитивный. Несмотря на то, что алгоритм Мамда­ни рекомендуют [3] применять в других областях, как-то экспертные си­стемы и системы принятия решений, он может эффективно работать и

66

при разработке нечётких СУ технологическим процессом, что будет по­казано ниже.

Как показали исследования [57], при включении НЛР с алгорит­мом Мамдани в анализируемую систему стабилизации целесообразно использовать его в качестве дополнительного канала управления, так как, для работы НЛР с данным алгоритмом в прямом канале управления потребовалось бы ввести в схему дополнительные динамические звенья.

Таким образом, НЛР с алгоритмом Мамдани выступает в каче­стве корректирующего элемента к основному закону регулирования.

Структурное решение показано на схеме (рис. 3.3). Здесь звено ДФ представляет собой динамический фильтр, выделяющий из сигнала ошибки е её производную по времени ё.е и подающий оба сигнала на НР. Ошибка регулирования и скорость её изменения являются наиболее ин­формативными для данного процесса управления, так как реализуется коррекция для ПИ-закона регулирования [10, 30, 35 - 38].

Рис. 3.3. Структурная схема нечёткой автоматизированной СУ температуры перегрева пара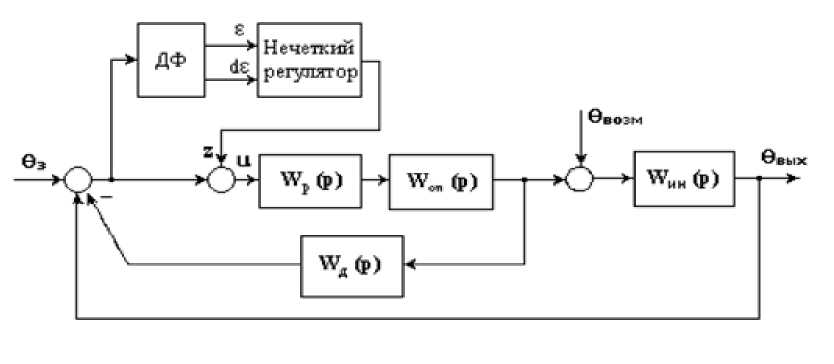

Нечёткий регулятор, включённый на параллельную коррекцию входного сигнала ПИ-регулятора, имеет два входа, один выход и выра­батывает сигнал коррекции г, в зависимости от состояния входных сиг-

67

налов e и de. С помощью сигнала коррекции нечёткий регулятор форси­рует работу основного регулятора.

Как отмечалось в предыдущей главе, нечёткий регулятор состоит из трёх основных блоков: блока фаззификации, блока нечёткого вывода и блока дефаззификации.

В первом блоке необходимо произвести фаззификацию входных сигналов, т.е. перевести чётко определённые сигналы в нечёткую форму. Для получения нечётких переменных необходимо инициализировать не­чёткие множества, соответствующие заданным входным сигналам.

Согласно [42], нечёткое множество A универсального множества E определяется как множество упорядоченных пар A{m_A(x)/x}, где m_A(x) - функция принадлежности, принимающая значения в упорядоченном мно­жестве M. Функция принадлежности указывает степень принадлежности элемента x подмножеству A.

Необходимо отметить, что если M = [0,1], а A есть нечёткое множе­ство, описываемое элементами из универсального множества E и множе­ством принадлежностей M, то нечёткое множество нормально, если его высота равна 1 (sup m_A(x)=1). При m_A(x) < 1 нечёткое множество называется субнормальным. Нечёткое множество является пустым, если VxeE m_A(x)= 0. Непустое субнормальное множество можно нормализовать по формуле

m _л (x) = ^ma(₎

sup m _A (x)

Нечёткое множество унимодально, если m_A(x) = 1 только на одном

x из E.

Носителем нечёткого множества A является обычное подмножество со свойством m_A(x) > 0, т.е. носитель A = {x/m_A(x)>0} VxeE.

Элементы хеЕ, для которых ти(х)=0,5, называются точками перехо­да множества А.

Средством, позволяющим связать любую физическую величину с каким-либо множеством, качественно характеризующим её значения, яв­ляется лингвистическая переменная.

Согласно [48, 49], для характеристики нечёткой переменной в отли­чие от лингвистической достаточно трёх параметров <а, X, А>, где а - наименование нечёткой переменной; X - область определения а; А - не­чёткое множество на X, описывающее ограничения на значения нечёткой переменной а.

Тогда, для двух входных сигналов итеративным методом зададимся нормальными непустыми подмножествами А/ (/=1...2; _/=1...5) с равно­значными точками перехода для А/ и А/+¹ на множестве Е Здесь индекс / соответствует количеству входов НЛР, а индекс ] - количеству используе­мых термов. Некоторый произвол при выборе количества термов обуслов­лен тем, что при возрастании количества термов возрастает объем базы правил, а существенного выигрыша в точности не наблюдается.

Формализуем лингвистические переменные р₁ и Ьг, где для <8₁, Т₁,

Х1, е, М> :

Ь - «ошибка»;

Т₁ - {«отрицательная большая», «отрицательная средняя», «нуле­вая», «положительная средняя», «положительная большая»};

^Х1 ^{- [х}1Ь ^х15^];

G₁ - процедура образования новых термов с помощью связок И/ИЛИ;

M₁ - процедура задания на Xi=[xn, x₁₅] нечётких подмножеств Л₁¹ =

2 3

«отрицательная большая», Л₁ = «отрицательная средняя», Л₁ = «нулевая», Л₁⁴ = «положительная средняя», Л₁⁵ = «положительная большая».

Тогда для <02, T2, X2, G₂, М2> :

ß₂ - «скорость изменения ошибки»;

Т₂ - {«отрицательная большая», «отрицательная средняя», «нуле­вая», «положительная средняя», «положительная большая»};

^X2 ^{- [x}2b ^x25^];

G₂ - процедура образования новых термов с помощью связок И/ИЛИ;

М₂ - процедура задания на X₂=[x₂₁, x₂₅] нечётких подмножеств Л₂¹ =

23

«отрицательная большая», Л2 = «отрицательная средняя», Л2 = «нулевая», Л2⁴ = «положительная средняя», Л2⁵ = «положительная большая».

Иллюстрация этапа формализации представлена на рис. 3.4, при этом вид функций принадлежности принят линейным, а их распределение равномерным, поскольку упреждающая коррекция НР должна быть равно­значной во всем диапазоне изменения динамической ошибки системы ста­билизации.

На рис. 3.4 используются следующие входные лингвистические пе­ременные:

e₁ - «ошибка»; е₂ - «скорость изменения ошибки».

Значение лингвистических переменных:

ОБ_{ - «отрицательная большая»;

OCi - «отрицательная средняя»;

Hi - «нулевая»;

ПС( - «положительная средняя»; ПБ_{ - «положительная большая».

Рис. 3.4. Функции принадлежности лингвистических переменных а) «ошибка» б) «скорость изменения ошибки»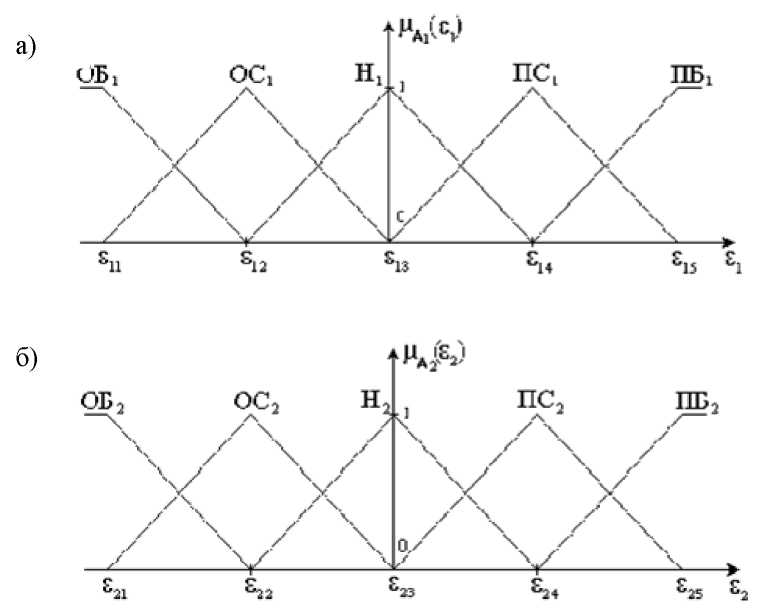

В терминах функций принадлежности результат этапа фаззифика- ции как значения лингвистических переменных запишется:

А⁼[тоБ(х_г)/ОБ, тос(х)юс_и тНх'1)1н_и дпсСх-упс, тшХупБ].

Содержательным компонентом блока нечёткого вывода является база знаний НЛР. Для заполнения первоначально пустой базы знаний, необходимо определить цели управления.

В данном случае целью управления является поддержание заданной температуры перегретого пара при возникновении контролируемых и не контролируемых возмущений. При этом чем быстрее увеличивается от­клонение температуры от заданного значения, тем интенсивнее должна осуществляться форсировка для максимально быстрой компенсации воз­никшего возмущения.

Таким образом, обеспечивается повышение быстродействия регу­лирующего воздействия и плавность изменения регулируемой величины вблизи заданного значения при изменении возмущающих воздействий быстрыми темпами.

В естественно-языковой форме управление будет следующим.

Если сигнал ошибки положительный и возрастает, то корректиру­ющий сигнал - положительный, а величина его пропорциональна величине скорости изменения ошибки. Если положительный сигнал ошибки умень­шается, то корректирующий сигнал - нулевой. Если сигнал ошибки отри­цательный и возрастает по абсолютной величине, то корректирующий сиг­нал - отрицательный, а величина его пропорциональна величине скорости изменения ошибки. Если отрицательный сигнал ошибки уменьшается по абсолютной величине, то корректирующий сигнал - нулевой.

Базу знаний нечёткого регулятора целесообразно формировать в виде продукций [14, 48, 50]. Получим множество управляющих правил, связывающих лингвистические значения входных и выходных переменных вида:

ЕСЛИ «ошибка» есть А/ И «скорость изменения ошибки» есть А2

ТО «коррекция» есть В,

где «коррекция» - наименование выходной лингвистической переменной

<г, Т₃,Х₃, G₃, М₃>, инициализированной, как показано на рис. 3.5.

Рис. 3.5. Функция принадлежности лингвистической переменной «коррекция»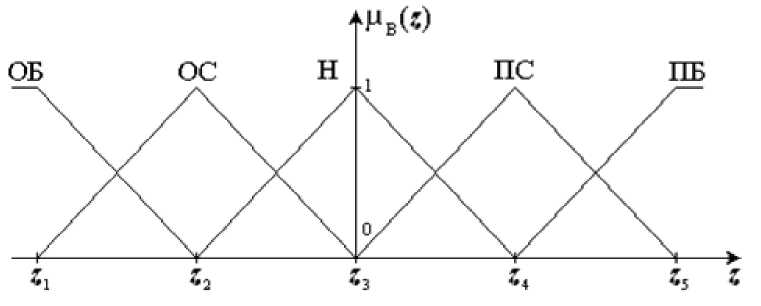

Для обеспечения однозначности между входной и выходной нечёт­кими переменными распределение функций принадлежности лингвистиче­ской переменной «коррекция» примем равномерным по диапазону её из­менения.

Зададим полный набор правил в таблице 3.1.

Таблица 3.1

База правил нечёткого логического регулятора

№	«ошибка»в1	«скорость изменения ошибки»е2	«коррекция»«
1	ОБ	ОБ	ОБ
2	ОС	ОС	ОС
3	Н	Н	Н
4	ПС	ПС	ПС
5	ПБ	ПБ	ПБ

Преобразуем области определений лингвистических переменных так, чтобы минимальное значение хц отобразилось в 0, т.е. [хц, х_г-₅]®[0, х₅- Хц]. Произведём нормирование на единицу, т.е. [0, х_г-5-Хц]®[0, 1]. Тогда значения лингвистических переменных будут задаваться нечёткими под­множествами на шкалах Ец Е₂, 2 табл. 3.2.

Таким образом, области значений лингвистических переменных

представляются девятью точками.

Таблица 3.2

Функции принадлежности лингвистической переменной

	0	0,125	0,25	0,375	0,5	0,625	0,75	0,875	1
ОБ	1	0,5	0
ОС	0	0,5	1	0,5	0
Н			0	0,5	1	0,5	0
ПС					0	0,5	1	0,5	0
ПБ							0	0,5	1

Основной задачей блока нечёткого логического вывода (по алго­ритму Мамдани) является получение множества значений функций при­надлежности для термов выходного сигнала, исходя из имеющегося мно­жества значений функций принадлежности для термов входного сигнала.

С помощью правил преобразования дизъюнктивной и конъюнктив­ной форм описание системы можно привести к импликативному виду X® У, где X и У - универсальные множества входных и выходных перемен­ных. Совокупность импликаций отражает функциональную взаимосвязь входных и выходных переменных и является основой для построения не­чёткого отношения Я:(Х®У), заданного на произведении (X х У).

Если на множестве X задано нечёткое множество А, то композици­онное правило вывода В = А • Я определяет на У нечёткое множество В с функцией принадлежности [14, 51]:

В в ⁽У⁾ = и (в А ^{(Х) Л} В Я ⁽- У⁾) .

X

Таким образом, композиционное правило вывода в этом случае за­дает закон функционирования нечёткой системы.

Для рассматриваемой системы приведём управляющие правила к виду ЕСЛИ (А/ х Л₂) ТО В, где (Л/ х А₂) - декартово произведение нечёт­ких множеств А] и Л₂, заданных на шкалах Е_/ и Е₂ с функцией принадлеж­ности:

т (А/х аі)^(є 1>^є 2 )= т А, (є 1 ^)л т _м(е 2),

определённой на Е_]хЕ₂.

Для каждого из правил вида ЕСЛИ (А/ х Л₂) ТО В, где (А/ х Л₂) - входное нечёткое множество, а В - соответствующее выходное нечёткое множество, определим нечёткое отношение В=(А/ х Л₂ )х В, і = 1.. .5 с функцией принадлежности:

т_к, ⁽⁽є,^є 2), _г⁾ = (т і ^(єі⁾ л т, ^(є 2 ^))л т_в, (?).

Совокупности всех правил соответствует нечёткое отношение:

5

В = и в¹,

і=1

с функцией принадлежности:

5

т в ^(є і,^є 2, ?)=и т в,(^(е і’^є 2⁾?⁾.

і=і

При заданных значениях входных переменных А/, Л₂ корректиру­ющее значение выходной переменной В определяется на основе компози­ционного правила вывода:

В = (А/ х А2) • В,

со степенью принадлежности:

тВ,^(г)= и и ⁽т_Лі⁽£і)лтлі^(є2⁾⁾лтв(е_и^є2,*)

ЄіЄ^Еі ^є₂ є^Е2 ^{1 2}

После процедуры нечёткого вывода, для получения реального вы­ходного сигнала нечёткого регулятора, необходимо осуществить процесс дефаззификации - перевод нечёткого значения z в чёткое значение z.

Исходя из гипотезы о том, что G определяется на конечном множе­стве высказываний U={ui,...u_n], числовое значение z по методу центра тя­жести можно получить согласно выражению:

N

Е ^zn т в ^(zn⁾

ry П = 1

= N

Е тв ^(zn⁾

n=1

где N= 9 - количество точек в Z (табл. 3.2).

Оценим базу знаний нечёткого регулятора на оптимальность через такие показатели, как полнота и непротиворечивость правил управления [43, 44, 48]. Наиболее часто требование полноты для системы продукций сводится к виду:

X = U SUPP Л;

i=1

где Supp Л_; - носитель нечёткого множества Л_;.

Это означает, что для каждого текущего состояния x процесса су­ществует хотя бы одно управляющее правило, посылка которого имеет ненулевую степень принадлежности для x.

Для рассматриваемой системы отсутствуют правила содержащие анцендент с нулевой степенью принадлежности (в табл. 3.2 нет столбцов, содержащих во всех ячейках только нули), следовательно, можно сделать вывод о полноте правил управления.

Непротиворечивость системы управляющих правил обычно тракту­ется как отсутствие правил, имеющих сходные посылки и различные или взаимоисключающие следствия.

Степень непротиворечивости _/-го и к-го правил можно задать вели­чиной:

с_]к = | иомз)^Л т* (^£1>)- и(;М^£2) ^лт* (^£2))1

Е ^{л л} е₂ ^{2 2}

Суммируя по к, получаем оценку непротиворечивости _/-го правила в системе:

С = 1С_м , 1<)<5 .

к=1

Если эта оценка превосходит некоторое пороговое значение, то правило из системы удаляется.

С₁₂ = 0.5 - 0.5 = 0.

С₂₄ = 0 - 0 = 0

С₁₃ = 0 - 0 = 0

С₂₅ = 0 - 0 = 0

Так для рассматриваемой системы (см. табл. 3.1, 3.2):

С₁₄ = 0 - 0 = 0

С₁₅ = 0 - 0 = 0

С₃₅ = 0 - 0 = 0

С₂₃ = 0.5 - 0.5 = 0,

С₄₅ = 0.5 - 0.5 = 0

С₃₄ = 0.5 - 0.5 = 0

Тогда:

С₁ = С₂ = С₃ = С₄ = С₅ = 0

То есть можно судить об абсолютной непротиворечивости системы управляющих правил.

Для оценки эффективности предложенного способа нечёткой кор­рекции системы стабилизации на рис. 3.6 приведены результаты модели­рования в среде «MATLAB» фирмы «The MathWorks Inc.» исходной си­стемы и системы с синтезированным корректором. При этом моделирова­ние производилось на основании экспериментальных данных автоматизи­рованной СУ температуры перегретого пара Комсомольской ТЭЦ-3. На рис 3.6 приведены 1 - график переходного процесса некорректированной системы (см. рис 3.2); 2 - с учётом нечёткой коррекции (см. рис 3.3).

Из графика видно, что применение нечёткого корректирующего ре­гулятора уменьшает как время реакции СУ температурой на внешнее воз­мущение, так и величину динамической ошибки (падение температуры уменьшается примерно на 30 %), а это в конечном итоге, повышает эконо­мичность работы, как турбины, так и энергоблока в целом.

Рис. 3.6. Результаты моделирования АСР температуры перегретого пара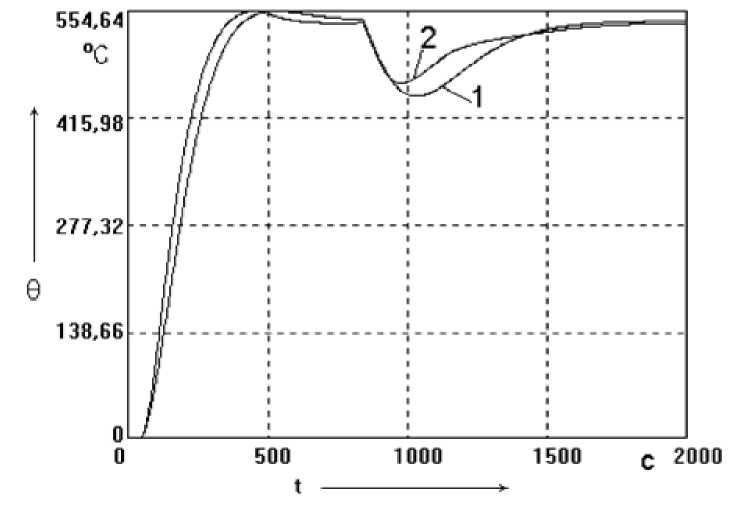

Использование в цепи обратной связи системы стабилизации звена реального дифференцирования с элементами ручной подстройки для реа­лизации режима упреждающей коррекции в ходе эксплуатации системы приводит к изменению соотношения постоянных времени дифференциру­ющей и инерционной частей звена, что, в конечном итоге, скажется на увеличении времени отработки возмущающих воздействий.

На рис. 3.7 приведены интегральные кривые изменения времени от­работки возмущающих воздействий при различных соотношениях выше­упомянутых постоянных времени для исходной и системы с нечёткой кор­рекцией, которые получены по результатам моделирования.

Рис. 3.7. Интегральные кривые изменения времени отработки возмущающих воздействий.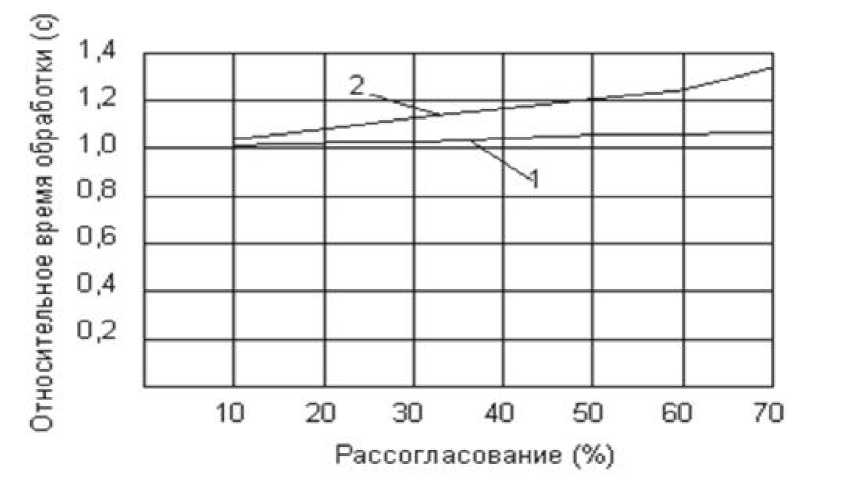

Как следует из приведённых кривых, введение нечёткой коррекции (нижняя кривая) обеспечивает время отработки возмущающих воздействий системой стабилизации примерно на одном и том уровне, независимо от соотношения постоянных времени. Таким образом, результаты моделиро­вания подтверждают правомерность выбранного подхода к синтезу систе­мы регулирования температуры и эффективность данного принципа кор­рекции.

2. Безэкспертные методы синтеза систем управления с нечёткой информацией

1. Оптимизация распределения функций

принадлежности НЛР

Анализ систем управления с нечёткими регуляторами говорит о том, что качественные показатели выходных координат системы управле­ния тепловыми процессами с НЛР зависят не только от количества функ­ций принадлежности нечёткого регулятора, их вида, но и от распределения их по диапазону регулирования. Задача выбора вида функций принадлеж­ности, распределения их по диапазону изменения входной координаты обычно возлагается на эксперта проектирующего НЛР и носит субъектив­ный характер. Ниже рассматривается метод оптимизации распределения функций принадлежности НЛР по диапазону изменения входной коорди­наты регулятора, позволяющий исключить субъективные факторы проек­тирования НЛР.

Объекты регулирования тепловых технологических процессов ха­рактеризуются существенной нелинейностью, наличием транспортного за­паздывания и значительной инерционностью звеньев регулирования [7, 13, 23, 24, 63]. При этом формализация их математического описания связана со значительными погрешностями, в то же время часть параметров систе­мы может быть описана не в количественных величинах, а в качественных. Это указывает на целесообразность реализации таких систем управления по нечёткому принципу.

Полагая, что динамика нечёткой системы управления тепловыми процессами описывается системой нелинейных дифференциальных урав­нений вида [59]:

.;(£) = Д?)х(£ - т) + В(?)м(?) + G(^)w(^ - в) + Н(;(£)),

где А(?) - матрица системы, Б(?) - матрица управления, G(^) - матрица возмущений, х(?) - координаты состояния системы, и(?) - сигнал управле­ния, w (?) - возмущающее воздействие, т - величина запаздывания обуслов­ленная внутренними параметрами объекта управления, в - величина за­паздывания обусловленная внешними возмущающими воздействиями, Н(х(?)) - составляющая, обусловленная нелинейными свойствами объекта регулирования, а НЛР, построенный по принципу Мамдани реализуется на основе трёх основных этапов фаззификация, база знаний (БЗ), дефаззифи- кация, то продукционные правила для случая с и-мерным входом и одно­мерным выходом НЛР могут быть записаны в виде:

Посылка: Если х₁ есть А^т ₁ и ... и х_п есть А^т_п Правило: Если Х1 есть А¹! и ... и х_п есть А¹_п то и есть Б¹ Вывод: и есть Б ,

Т

где [Х1,х2,...,х_п ] = х - вектор входного сигнала, и - скалярная величина

сигнала управления. X является универсумом для каждой лингвистической переменной х_г, а и - соответственно универсумом и. Обозначая значения

г-ых лингвистических переменных х_г и и через А^у и Б^] , ] = 1, т соответ­ственно получим значения функции принадлежности ц _{А у} (х): Хг ® [0,1] и

^Аг

^тБ]^(и)^{: и} ® [0,1].

Нечёткое отношение для каждого продукционного правила опреде­ляется следующим образом:

(А ₁ и А ₂ и ... и А _п)^Б^] ,

т_К] ⁽*1^, х2 ^хп^,и) = т_А]^(хі⁾т_А]^(х2 ⁾-т_А] ^(хп ⁾т_Б]^(и),

нечёткое отношение Б для т правил определяется согласно выражению:

т

т Б (*1, х 2,..., *п , и) = тах т _Б] (х_ь X 2,..., *п , и).

]=1 ^Б

В случае, когда лингвистические переменные входного сигнала принимают нечёткие множества Д,7 = 1, п нечёткое множество В лингви­стической переменной сигнала управления определяется при помощи не­чёткой импликации. Функция принадлежности для В имеет вид:

т _В О)

		п	п	“Г
П т Д (х7 )		тах _ 1=1	П т Д1 (Х7 ) _7=1 7 _	•т в1 —' ^

тах

^х1, ^х2 5*"' ,^хп

Пусть нечёткие подмножества В¹ имеют вид:

т _В ⁽и⁾

1, и = 1 0, и Ф1

где 1 - дискретные численные значения выходного сигнала* Тогда с учё­том этого:

^т В ^(и)

На этапе дефаззификации применяя метод центральной площади, получим выражение, определяющее значение выходного сигнала:

т

и =

1=1 и=1

т п

^ П ^т Д^{1 (Х}7 ⁾

1=17=1 ⁷

Обозначим:

п

П ^т Д1 ^(Х7 ⁾

7=1 ⁷

т п

2 П ^т Д^{1 (Х}7 ⁾

1=17=1 ⁷

тогда формула определения выходного сигнала НЛР (сигнала управления) будет иметь вид:

_ т .

и(X, 1) = ^ 1С у (X) = 1 С (X).

у=1

Таким образом, в случае полноты и непротиворечивости БЗ, со­гласно полученному выражению НЛР может быть описан в виде произве­дения двух функций определяемых видом и распределением по диапазону регулирования функций принадлежности и выбранным алгоритмом нечёт­кого вывода.

Если положить, что объект управления описывается упрощёнными математическими выражениями и известны критерии оптимизации, то можно найти выражение для желаемого управляющего воздействия обес­печивающего требуемые показатели качества. В общем виде, функционал качества, на основании которого может быть получено требуемое управ­ляющее воздействие, имеет вид:

¥г = /^[

т²у²(Ф) + с²Ф²(і) іі.

где т, с - постоянные коэффициенты, Ф(£) - произвольная дифференци­руемая или кусочно-непрерывная функция и Ф(0) = 0, у(Ф) - однознач­ная, непрерывная, дифференцируемая "Ф функция, при чем у(0) = 0 и у(Ф) • ¥ < 0 при "Ф Ф 0.

1	1 г? го 1	-1 г
ь	1 а і

и = -

1

Т

г(ф)+ Т

к=1

дФ ( X )

дхк

1к^(х) •

Минимизация данного функционала требует от НЛР реализации выходного сигнала вида:

Если считать, что база знаний полна и непротиворечива, то НЛР позволяет реализовать требуемый закон управления максимально прибли­женный к желаемому и зависящий от Я и £(X)• Положив, что вектор

50. = const, синтез НЛР можно свести к оптимальному распределению функций принадлежности при их фиксированном числе.

Поскольку вид ФП и их распределение по диапазону регулирования описываются логическими элементами, то для синтеза НЛР целесообразно использовать математико-логический подход с применением универсаль­ной шкалы, предложенной в [49].

Задача синтеза должна сводиться к отысканию такого вида и формы ФП, которые при выше приведённых допущениях обеспечивали бы, на ос­новании принятого алгоритма нечёткого вывода, требуемый вид управля - ющего воздействия.

При известном управляющем воздействии, заданном входном сиг­нале регулирования, задача будет заключаться в нахождении желаемой функции отображения [48, 52]. Для поиска функции отображения введём ряд ограничений.

1. Будем считать, что реализация желаемого закона управления осуществляется по одному входному сигналу НЛР. Второй входной сигнал НЛР может быть учтён впоследствии, как корректирующий.

2. Поскольку для практического большинства используемых устой­чивых систем управления тепловыми процессами вид динамических пере­ходных характеристик может быть сведён к двум типам: апериодическому и колебательному, то дальнейшие рассуждения будем проводить для этих случаев.

у

X

Рис. 3.8. Обобщённая координатная

Для доказательства этого рассмотрим систему координат (рис.3.8), правая часть которой представляет собой единичный квадрат x ® [0;1] и ^y ®^[0;1].

система

Диагональ этого квадрата является базовой функцией отображения %₀ или осью отображения, при которой равномерно распределённые по оси абсцисс ФП, отражаясь на ось ординат, не претерпевают никаких измене­ний. Пусть спрогнозированный или полученный из каких-либо других со­ображений выходной сигнал НЛР, являющийся сигналом управления име­ет вид рис. 3.9 а, б.

Рис .3.9. Законы управления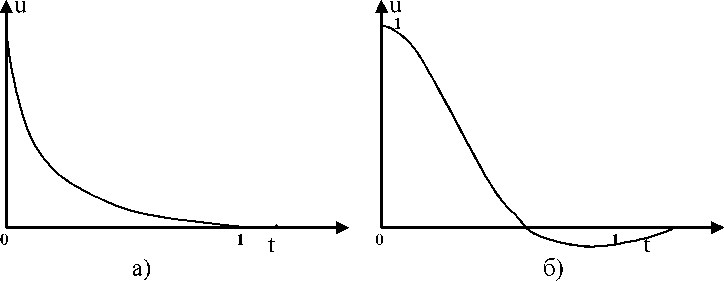

Преобразуем сигнал управления, например, приведённый на рис. 3.9, б, в функцию вида % = и(—ї) что соответствует прохождению сиг­нала управления сквозь структуру НЛР в обратном направлении рис. 3.10.

Рис.3.10. Преобразованный сигнал управления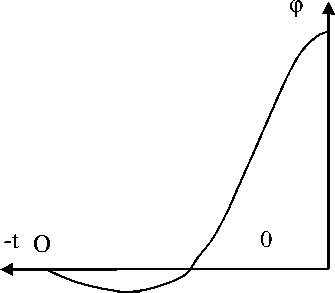

Учитывая, что выходной сигнал НЛР в конце переходного процесса стремится к нулю, то функция отображения должна стремиться к своему максималь­ному значению. Сориентируем данную функцию в правой части таким образом, чтобы касатель­ная к точке О определила угол поворота координатной системы

Ф - функции отображения. Такой касательной является ось абсцисс на рис. 3.11.

Рис. 3.11. Координатная система отображения функций принадлежности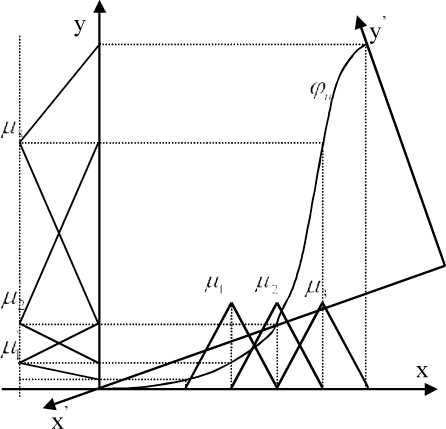

Приведённый вид функции отображения изменит равномерно распределённые ФП на заданном диапазоне - концентрируя их в окрестности нуля и соответствен­но растягивая их в крайних пре­делах диапазона.

Поскольку в окрестности начала координат, синтезируемые ФП стягиваются в линию, то про­цесс их построения (при количе­стве ФП больше 9), целесообраз­но завершить при попадании зна­чения х в зону соответствующую классической зоне завершения пере­ходного процесса. С другой стороны применение большого числа ФП (> 9 ) является неоправданным, т.к. приводит к значительному росту алгорит­мической сложности НЛР, и обрабатываемой информации.

Данный алгоритм оптимизации распределения функций принад­лежности НЛР реализован в виде программного обеспечения [58]. Средой разработки является язык технических вычислений Ма1;ЬаЬ. Этот выбор обусловлен наличием соответствующего встроенного инструментария.

Разработанная программа позволяет не только автоматизировать процесс настройки НЛР, но и проводить исследование систем управления с нечётким управлением. Пользователь имеет возможность по задаваемой аналитически или полученной при моделировании желаемой переходной характеристике управляющего сигнала для произвольно числа функций

принадлежности получить оптимальную настройку блоков фаззификации и дефаззификации нечёткого логического регулятора и далее исследовать анализируемую систему на модели в среде Ма1;ЬаЬ.

Пример экранной формы интерфейса пользователя приведён на рис. 3.12.

Таким образом, приведённая методика синтеза алгоритма решает одну из проблем автоматизации основных этапов настройки НЛР (фаззи- фикация, дефаззификации). Предлагаемый подход позволяет получить же­лаемые показатели качества регулирования за счёт применения средств вычислительного интеллекта без потерь точности.

Рис. 3.12. Интерфейс пользователя программы МаШаЪ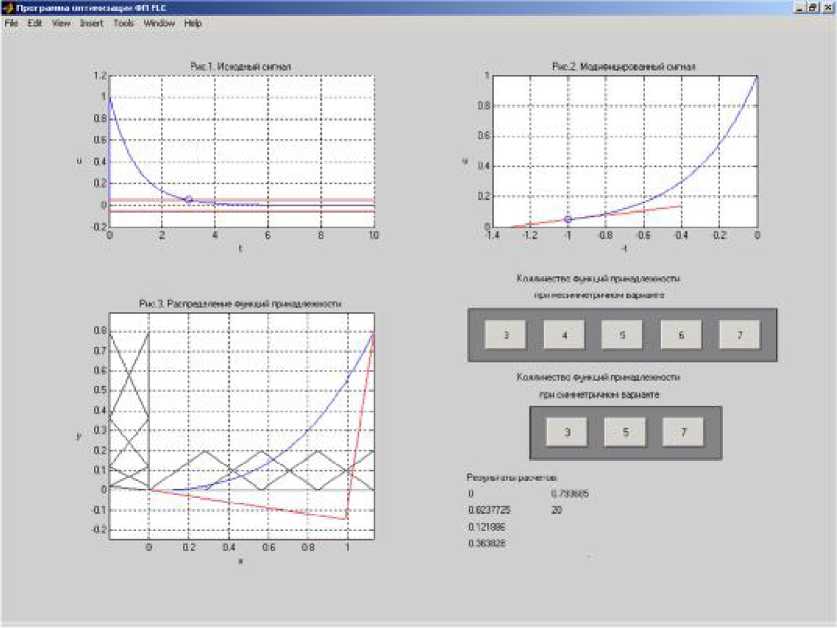

2. Синтез НЛР по прямым показателям качества

Как было отмечено ранее, синтез НЛР состоит из настройки трёх

взаимосвязанных блоков (фаззификация, БЗ, дефаззификация), при этом

формирование второго блока базируется на методах представления и по-

87

иска знаний. Основная роль в этом процессе отдаётся оператору-эксперту, в качестве которого выступает квалифицированный специалист или знаю­щий данную предметную область инженер. Т.е. и в данном случае процесс составления БЗ носит субъективный характер.

Важным условием эффективного функционирования НЛР является построение непротиворечивой и оптимально полной БЗ. При этом зача­стую, адекватность БЗ зависит от величины среза объёма выборки экс­пертных оценок, что является в большинстве случаев взаимоисключаю­щим фактором.

Как известно из теории экспертных систем [31, 40, 41, 61], функци­онирование БЗ осуществляется с надстроенной машиной логического вы­вода (МЛВ), которая представляет собой механизм рассуждений, опери­рующий знаниями и с целью получения новых знаний. Для этого обычно используется программно реализованный механизм дедуктивного логиче­ского вывода (какая-либо его разновидность) или механизм поиска реше­ния в сети фреймов или семантической сети. МЛВ может реализовывать рассуждения в виде:

• дедуктивного вывода (прямого, обратного, смешанного);

• нечёткого вывода;

• вероятностного вывода;

• поиска решения с разбиением на последовательность подзадач;

• поиска решения с использованием стратегии разбиения простран­ства поиска с учётом уровней абстрагирования решения или понятий, с ними связанных;

• монотонного или немонотонного рассуждения,

• рассуждений с использованием механизма аргументации;

• ассоциативного поиска с использованием нейронных сетей;

• вывода с использованием механизма лингвистической переменной.

Задачи принятия решений в условиях определённости характери­зуются наличием полной и достоверной информации о проблемной ситуа­ции, целях, ограничениях и последствиях принимаемых решений. В таких задачах заранее, в процессе анализа, известно, к какому исходу приведёт каждая из стратегий. В частности, это означает, что все факторы известны, учтены и не могут каким-либо непредвиденным образом повлиять на ис­ход операции. В этом случае МЛВ настраивается на работу с классически­ми методами, такими как фреймы и механизмы дедуктивного логического вывода.

В отличие от отмеченного, характерной особенностью задач приня­тия решений в условиях неопределённости является то, что исход опера­ции зависит не только от экспертов (лиц принимающих решения) и фикси­рованных факторов, но и от слабо определённых показателей, неконтроли­руемых экспертами и (или) недостоверно известных им в момент принятия решения. В результате каждая экспертная стратегия оказывается связанной с множеством возможных исходов итоговой операции, что существенно усложняет процедуру выработки решения. Для приведённого класса задач наилучшим образом подходит настройка МЛВ на нечёткий вывод.

Должное функционирование МЛВ, настроенной на нечёткий вывод, требует при формировании и обновлении БЗ соответствующих экспертных стратегий. Поэтому является необходимым проанализировать основные экспертные стратегии с соответствующими критериями оценок, позволя­ющие обеспечить адекватное решение поставленной задачи в условиях не­определённости:

1. Согласно минимаксному критерию Вальда, оптимальным счита­ется вариант решения, в случае, когда составление продукционных правил БЗ определяет вариант наихудшей настройки реакции системы (установка системы на границу устойчивости). При этом аналитически он может быть представлен как:

v_w = max min a_ij-, i j

где ^aij - величина весового коэффициента продукционного правила. Дан­ный критерий отражает позицию крайнего пессимизма, т.е. всегда ориен­тируется на худшие условия, обеспечивая тем самым избыточность БЗ.

2. Максиминный критерий представляет собой критерий абсолют­ного оптимизма и связан с потерей части информации о системе:

v_M = max min a_ij- i j

3. Для Критерия двойственности Гурвица характерно то, что при выборе правила из БЗ, вместо двух граничных решений при оценке ситуа­ции, необходимо придерживаться некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего, благопри­ятного поведения системы. Согласно данному подходу, для каждого пра­вила необходимо определить линейную комбинацию минимальных и мак­симальных значений консеквента и выбрать ту комбинацию, для которой эта величина окажется наибольшей:

v_H = max

i

a • max a_ij + (1 - a) min a_ij

i

j J

где a - «степень оптимизма» , 0< a <1 (при a=0 критерий Гурвица тожде­ственен критерию Вальда, а при a=1 совпадает с максиминным решением). При этом, на выбор значения степени оптимизма оказывает влияние мера ответственности: чем серьёзнее последствия ошибочных решений, тем больше желание принимающего решение застраховаться, т.е. степень оп­тимизма a, как правило, ближе к нулю.

4. Критерий Сэвиджа в общем виде является критерием риска min- max. Зачастую на практике [18], выбирая одно из возможных правил, оста­навливаются на том, осуществление которого приведёт к наименее тяжё-

лым последствиям, если выбор окажется ошибочным. По принципу Сэви­джа выбор каждого правила характеризуется величиной дополнительных потерь, которые возникают при реализации этого правила, по сравнению с бездействием системы в данном состоянии. При этом правильное решение не влечёт за собой никаких дополнительных потерь, и величина этих по­терь равна нулю. Таким образом, при выборе правила, следует принимать во внимание только дополнительные потери, которые являются следстви­ем ошибок выбора. Для формализации задачи принятия решения строится так называемая «матрица рисков», элементы которой показывают, какой недостаток получится в результате выбора неоптимального правила. Сте­пень риска субъекта Гу при выборе величины весового коэффициента про­дукционного правила называется разность между максимальным результа­том от действия правила у, который можно получить в этих условиях и ре­зультатом, который получит субъект в тех же условиях, в случае действия правила і. Если бы субъект знал заранее будущую реакцию системы на правило у, он выбрал бы стратегию, которой соответствует максимальный элемент в данном столбце: таха.., тогда степень риска равняется

і ^J

= maxa_tj - aj. Таким образом, критерий Сэвиджа рекомендует в усло-

i виях неопределённости выбирать решение, обеспечивающее минимальное значение максимального риска:

^aij ⁾,

v_s = min max r_ij = min max(max a_ij

ⁱ j ⁱ j

5. В ряде случаев представляется правдоподобным следующее рас­суждение: так как неизвестны будущие состояния системы, то можно счи­тать их равновероятными. Этот подход к решению используется в крите­рии «недостаточного основания» Лапласа. При решении задачи для каждо­го случая подсчитывается математическое ожидание благоприятного исхо-

да (вероятности состояний полагаются равными у ,■ = у , j = 1,n), и вы-

J / YI

бирается то правило, при котором величина этого исхода максимальна.

V 1 1 V

v_L = max V~ ^aj =~ ^max V ^aj i n ^J n i ^J .

6. Критерий Байеса-Лапласа отступает от условий полной неопре­делённости - он предполагает, что возможным состояниям можно припи­сать определённую вероятность их наступления и, определив математиче­ское ожидание благоприятного исхода для каждого решения, выбрать то, которое обеспечивает наибольшее значение благоприятного исхода:

^vBL = ^max V ^aijyj

Этот метод использует возможность анализа предварительной ин­формации о состояниях системы, при этом предполагается как повторяе­мость состояний, так и повторяемость решений, и, прежде всего, наличие достаточно достоверных данных о прошлых состояниях. То есть, основы­ваясь на предыдущих наблюдениях, предоставляется возможным прогно­зирование будущего состояние.

Следует отметить, что рассмотренные критерии экспертных страте­гий не исчерпывают всего многообразия критериев выбора решения [21], но в рамках представляемой работы, это следует считать достаточным для проведения следующего вывода:

В силу своей природы, отмеченные стратегии только частично направлены на решения задач в условиях неопределённости [32]. Тем са­мым, проблема выбора решения при слабоструктурированном информаци­онном потоке является достаточно неоднозначной, так как отсутствует возможность предварительного анализа вектора событий достаточного объёма. Выбор критерия (как и выбор принципа оптимальности) является наиболее трудной и ответственной задачей в теории принятия решений. Следует отметить, что конкретная ситуация никогда не бывает настолько

92

неопределённой [49], чтобы нельзя было бы получить частичной информа­ции относительно вероятностного распределения состояний. В этом слу­чае, оценив распределение вероятностей состояний, применяют альтерна­тивный - байесовский подход, либо проводят эксперимент, позволяющий уточнить поведение исследуемой системы.

Учитывая тот фактор, что тепловые процессы характеризуются не­прерывными и монотонными временными зависимостями и желаемый вид данных зависимостей для конкретного объекта регулирования по извест­ному его упрощённому математическому описанию практически всегда известен, то можно предложить несколько иной метод формирования БЗ НЛР.

Полагая известными динамические показатели выходной координа­ты синтезируемой замкнутой СУ, при этом переходная характеристика этой координаты является монотонной непрерывной и сколь угодно раз дифференцируемой. Задачу синтеза НЛР для данного класса систем управ­ления можно сформулировать следующим образом [15]:

Пусть желаемая, нечёткая замкнутая автоматизированная СУ опи­сывается в виде

У = (X, У),

где X, У - лингвистические значения нечётких входных и выходных пере­менных; Г_ж - нечёткий оператор, заданный в виде набора управляющих правил

если Х есть А и У есть В, то У есть С

Объект регулирования для таких систем, принимая во внимание принцип последовательной коррекции, может быть представлен или в виде

У = р_о (У ,и),

или в виде звена второго порядка

У = Го (У ,У ,и),

при этом Г_а - нечёткий оператор, записанный в виде управляющих правил, и - лингвистическое значение нечёткой переменной управления на входе объекта регулирования.

Цель синтеза по известным нечётким операторам Г_ж и ¥_а найти не­чёткий оператор регулятора ¥_р, который обеспечит требуемое качество ди­намических характеристик автоматизированной СУ.

Лингвистический подход формирования оптимального оператора желаемой СУ можно сформулировать из утверждений: чем больше рассо­гласование между задающим воздействием Х и выходным значением У, тем больше должна быть величина изменения этого рассогласования или, что равнозначно, должна быть выше скорость изменения выходной пере­менной У, но с противоположным знаком. При этом не выдвигается ника­ких ограничений ни на количество терм-множеств лингвистических пере­менных ни на их вид и их распределение по всему диапазону изменения переменной.

Из вышеприведённого утверждения следует, что для реализации ал­горитма синтеза НЛР необходимо иметь информацию как об ошибке жела­емой СУ, так и о её производной. При известной динамической характери­стике выходной координаты желаемой СУ и известном входном воздей­ствии такую информацию получить несложно. Но данной информации для реализации алгоритма недостаточно. Поскольку переходную характери­стику выходной координаты СУ, а, следовательно, и её ошибку (е = х - у) можно представить из участков разгона и торможения, плавно переходя­щих один в другой, для которых производная имеет различный знак, в ко­нечном итоге выделение терм-множеств входной и выходной лингвистиче­ских переменных приводит к возникновению противоречия. Для исклю­чения данного противоречия введём информацию о второй производной ошибки желаемой СУ, поскольку нулевое значение этой производной бу­дет соответствовать смене знака производной ошибки, т.е. точке перехода

94

с участка разгона на участок торможения или наоборот, а максимумы этой производной - точкам перехода с участка разгона на участок торможения для производной ошибки.

Алгоритм синтеза НЛР будет сводиться к следующему [5, 54]:

Координатная плоскость, на которой изображены кривые е(і), е(і), е\і) и Х(і) в относительных единицах, разбивается на зоны в следующем порядке. Из точек пересечения кривой е"(і) с осью абсцисс восстанавлива­ем перпендикуляр до пересечения с кривой е(і) и из полученных точек проводим прямые, параллельные оси абсцисс к₁, к₂. Из точек, соответству­ющих максимумам кривой е"(і), восстанавливаем перпендикуляры до пе­ресечения с кривой е(і) и из полученных точек проводим линии к₃, к₄, па­раллельные оси абсцисс (см. рис. 3.13).

Затем из точек пересечения прямых к₁ - к₄ с кривыми ошибки си­стемы е(і) и её производной е(і) проводим прямые /₁, /₂, 1₃, ... параллель­ные оси ординат. Таким образом, на координатной плоскости прямыми к - /■ формируется сетка, на основании которой определяется нечёткий опе­ратор А_ж. Так например, для зоны, отмеченной на рис.2.33 (*,**) строка нечёткого оператора Е_ж будет выглядеть следующим образом (табл. 3.3).

Таблица 3.3

База знаний строки нечёткого оператора

е'	е
	/р	/п
/п	8р
		8р
8р	X

где /п - отрицательное большое; sn - отрицательное малое; sp - положи­тельное малое; тр - положительное среднее; /р - положительное большое, или в виде строки правил:

Если е есть /п и е есть тр то X есть 8р (*);

95

Если е есть 8р и е есть 8П то Xесть 8р (**);

Такой подход позволяет автоматически производить выбор количе­ства терм-множеств лингвистических переменных, а также определить диапазоны их изменения.

Рис. 3.13. Диаграмма формирования правил нечёткого регулятора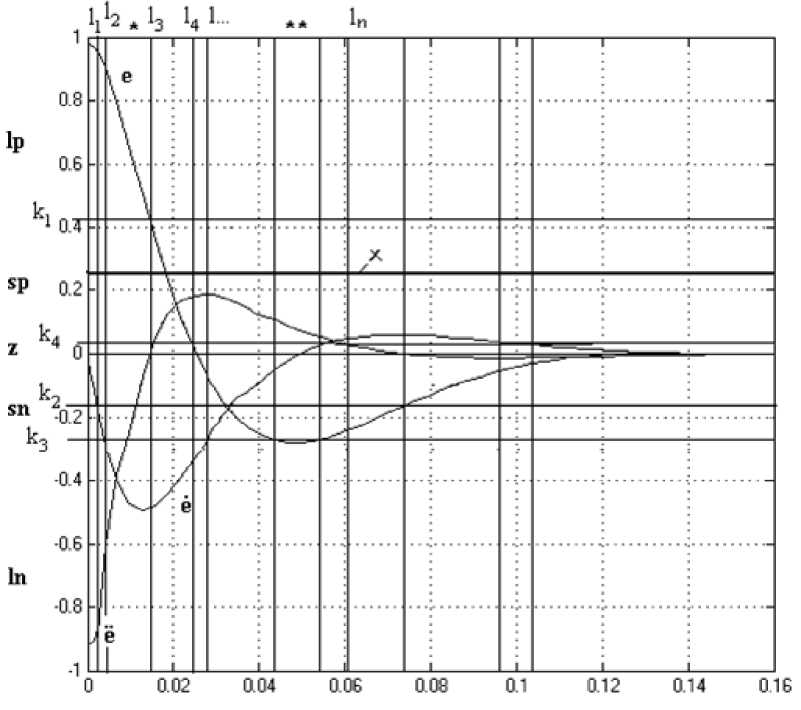

Аналогично может быть построен и нечёткий оператор объекта ре­гулирования А₀. Тогда формирование нечёткого оператора регулятора ¥_р сведётся к следующему. Для произвольно выбранных значений X и У в

наборе ¥_ж находим У , затем, используя полученное значение У и ранее принятое значение У, а также набор соотношений А₀, находим значение и. Таким образом, получаем один параметр соотношения и = ¥_р (X, У) = ^ (е). Повторяя вышеописанные действия с остальными значениями лингвисти-

ческих переменных X и У, определяем весь набор параметров нечёткого оператора ¥_р.

Использование такого подхода к проектированию НЛР не исключа­ет возможности получения БЗ, не удовлетворяющей условию о непротиво­речивости наполняющих её правил. Как известно [84, 94], непротиворечи­вость системы управляющих правил обычно трактуется как отсутствие правил, имеющих сходные посылки и различные или взаимоисключающие следствия. При этом степень непротиворечивости 7-го и к-го правил можно оценит выражением:

С, = І ЦЮ“* (^£і)^л(£]))-Ц“ (е2) лт₄(£2))!.

Е ^{1 1} Е2 ^{2 2}

Для проверки правильности предлагаемой методики синтеза НЛР на рис. 3.14 приведены результаты моделирования системы регулирова­ния, настроенной на «модульный» оптимум, т.е. системы регулирования, переходная характеристика которой имеет слабо колебательный харак­тер. При этом с целью понижения алгоритмической сложности НЛР ко­личество терм - множеств лингвистической переменной ошибки было ограничено четырьмя, для наиболее значимых участков. С этой же це­лью количество правил базы знаний было снижено до 10. Кривые моде­лирования наглядно иллюстрируют совпадение переходной характери­стики системы с НЛР с переходной характеристикой исходной системы даже при ограничениях на алгоритмическую сложность БЗ НЛР.

Рис. 3.14. Результаты моделирования СУ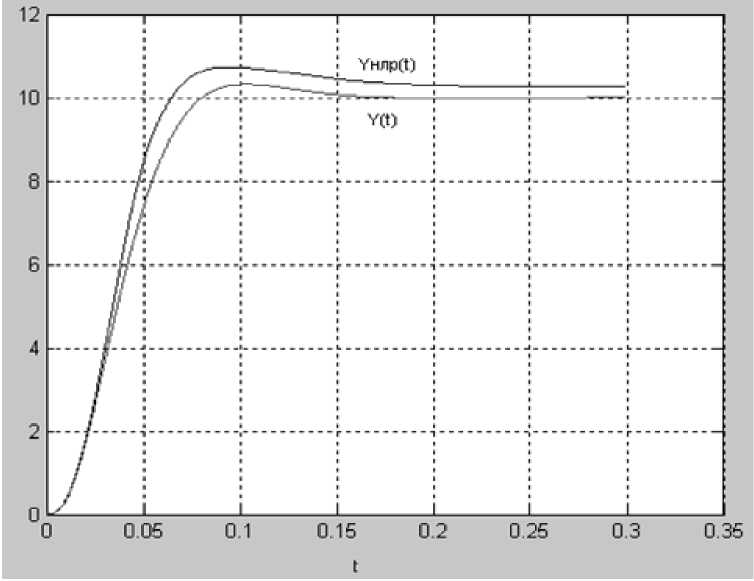

Таким образом, приведённый подход к построению БЗ НЛР, позво­ляет проводить её настойку, исключив фактор субъективности. Кроме то­го, необходимо отметить, что применение вышеизложенного метода сни­жает погрешности связанные с ранее описанными статистическими мето­дами и легко поддаётся алгоритмизации. Полученная с применением мето­да БЗ НЛР всегда удовлетворяет требованию полноты, поскольку её фор­мирование реализуется по прямым показателям качества.

С целью автоматизации процесса синтеза НЛР по прямым показа­телям качества, исключения графоаналитических приёмов построения и придания исследовательских функций при использовании данного метода разработан программный комплекс, работающий в среде Ма1;ЬаЬ [55].

Код программы представлен в виде двух т-файлов, реализующие соответственно две функции.

Первая функция реализует непосредственно алгоритм поиска крити­ческих зон. Аргументами (входными данными) для этой функции являются соответственно желаемые сигналы на входе и выходе регулятора изменяе­мые во времени. Выходные данные сформированы в виде структуры, кото­рая содержит в себе найденные точки смены функций принадлежности по сигналу на входе регулятора, по его производной и по сигналу на выходе регулятора. Результаты отображаются в диалоговом графическом окне (см. рис. 3.15), в котором можно менять точность поиска точек перегиба.

Вторая функция реализует непосредственно построение базы НЛР: производит формирование функций принадлежности, причём сначала, по умолчанию, они берутся симметричные и треугольной формы; производит­ся формирование базы правил; строятся на одном графическом поле желае­мая переходная функция и её аналог, полученный с помощью НЛР; вычис­ляется среднеквадратичная ошибка; так же, если необходимо, можно отоб­разить трёхмерную поверхность отклика базы правил (на два входа и один выход). Графическое окно второй функции изображено на рис. 3.16. Таким образом, из рис. 3.16 видно, что реализована возможность коррекции как функций принадлежности (положение вершины отдельной функции, её ви­да), так и базы правил (смена условия в антенценденте, смена метода деф- фазификации).

Выходные данные второй функции формируются в виде структуры, которая представляет собой базу знаний НЛР. Эта структура сохраняется в рабочей области MatLab под именем “fis” и может быть тут же использо­вана без дополнительных преобразований при моделировании в Simulink.

Смите э-НЛР

Р*е Бок Мет Jn.fr!> ТооЬ Мгяо« Нар

-0.5

Нгес15юп от зеагсп:

зп! тп огаме МР теп

С1|к

А РЕ ЗУЛЫ АГЫ РАСЧЁТОВ А

Прямые П.ЗрЙЛЛеЛ1^*)1е 0Н'1абЦНС

11-0.194025 11 0.673344 110.0623352

2 0.098574 21 -0333136 21 (14 30563

Э 0Б00306 310.095332 3 1696448

□|к-(о-С1о5в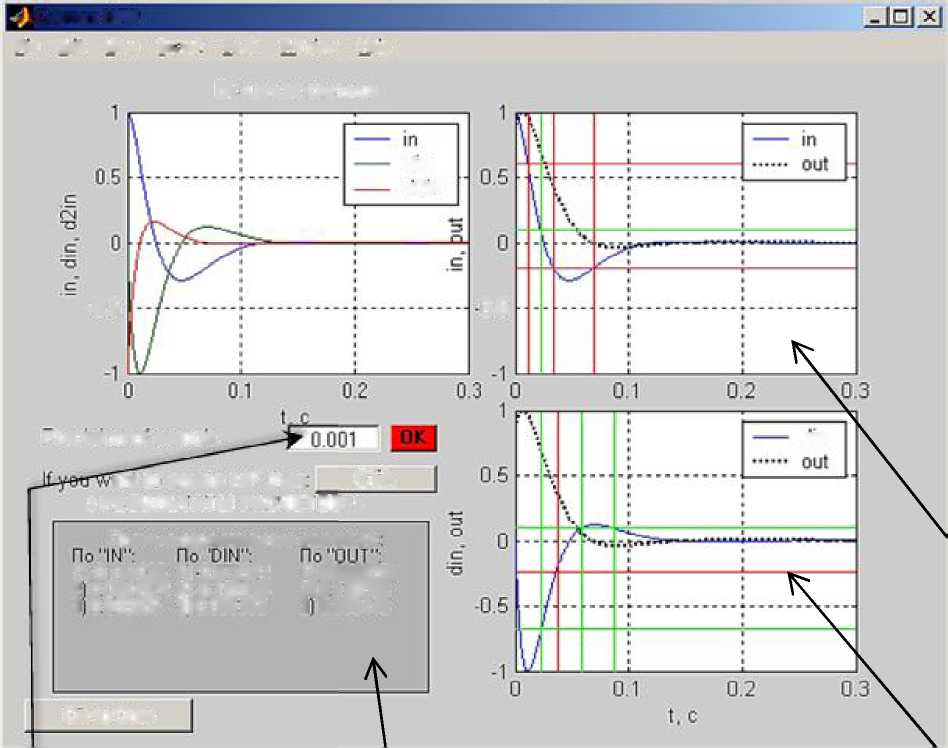

Точность поиска

Окно результатов

dln

а 2т

□.5

от

Формирование сетки для определё- ния ф-й принадлежности для сигна­лов вход-выход, производная от входного сигнала - выход соответ­ственно.

Рис. 3.15. Графическое окно первой функции

Входной сигнал