В.А. Соловьев, С.П. Черный

ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ В ЗАДАЧАХ УПРАВЛЕНИЯ. ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

Комсомольск-на-Амуре

2010

Министерство образования и науки Российской Федерации Г осударственное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет»

В.А. Соловьев С.П. Черный

ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ В ЗАДАЧАХ УПРАВЛЕНИЯ. ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНОЛО- ГИЧЕСКИМИ ПРОЦЕССАМИ

Учебное пособие

Рекомендовано УМО РАЕ по классическому университетскому и техническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальностям: 220201 — «Управление и информатика в технических системах»; 140604 — «Электропривод и автоматика промышленных

установок и технологических комплексов»

Комсомольск-на-Амуре

УДК 681.51.011:004.89:002.53 ББК 31.2+32 А954

Рецензент:

М.П. Дунаев, доктор технических наук, профессор кафедры «Электропривод и электротранспорт» ГОУВПО «Иркутский государственный технический университет»;

А954 Соловьев В. А. Искусственный интеллект в задачах управле­

ния. Интеллектуальные системы управления технологически­ми процессами : учеб. пособие / В. А. Соловьев, С.П. Черный. - Владивосток: Дальнаука, 2010. - 267 с.

ISBN 978-5-8044-1120-7

Представлены основные положения теории мягких вычислений. Рас­смотрены методики безэкспертного синтеза основных блоков нечётких ло­гических регуляторов с использованием различных алгоритмов нечёткого вывода для управления различными технологическими процессами, а так­же методики проектирования нечётких регуляторов для компенсации не­линейностей искусственного и естественного характера. Приведены ими­тационные модели различных нечётких систем с применением языка ин­женерных вычислений MatLab.

Для студентов, специалистов, магистров, аспирантов и научных ра­ботников, работающих в области исследования интеллектуальных систем управления технологическими процессами.

УДК 930.25:94(571)(07)

ББК 63.2я7

ISBN 978-5-8044-1120-7 © Г осударственное образовательное

учреждение высшего профессиональ­ного образования «Комсомольский-на- Амуре государственный технический университет», 2010

UDC 681.5.01:658.5; 681.5.01:658.512

Soloviev V.A.,Cherniy S.P. Artificial intelligence in the tasks of control. Intel­ligent control systems of technological processes. - Vladivostok: Dalnauka, 2010 - 267 p.

ISBN 978-5-8044-1120-7

Basic propositions of the theory of soft computing are presented. The methodologies of without-expert synthesis of main blocks of fuzzy logical con­trollers with using different algorithms of fuzzy inference for control various technological processes, as well as the methodologies of design of fuzzy control­lers for compensation of the nonlinearities of artificial and natural character are considered. Simulation models of different fuzzy systems are given, using the language of technical computing MatLab.

For the students, specialists, masters, post-graduates, scientist working in the sphere of research intelligent control systems of technological processes.

Keywords: fuzzy logic, fuzzy controller, intelligent control system, com­pensation of nonlinearities, simulation model, technological process.

Scientific editor:

Doctor of engineering sciences, professor N.A.Taranukha. SEIHPE KnASTU

Art editor:

A.I. Nosachenko

Reviewer:

Doctor of engineering sciences, professor M.P.Dunaev. SEIHPE IrSTU

Translation into English: A.S.Meshkov, SEIHPE KnASTU

ISBN 978-5-8044-1120-7

© S.P. Cherniy, V.A. Soloviev

Глава 4. Принципы компенсации нелинейностей систем

Учебное пособие предназначено для студентов специальностей 220201 - «Управление и информатика в технических системах»; 140604 - «Электропривод и автоматика промышленных установок и технологиче­ских комплексов», а также рекомендуется преподавателям в качестве под­готовительного материала к лекциям и студентам других специальностей самостоятельно изучающих принципы интеллектуального управления раз­личными объектами.

Несмотря на большое количество технической литературы в области интеллектуальных систем управления имеется ряд аспектов, которые по­будили авторов к написанию данного пособия:

• отсутствует систематизированный подход к проектированию си­стем управления технологическими процессами базирующийся на теории мягких вычислений;

• не изложены принципы синтеза нечётких логических регуляторов с использованием безэкспертной оценки основных параметров существенно снижающих влияние субъективного фактора;

• не описаны принципы использования подхода с применением тео­рии нечётких множеств для компенсации однозначных и неоднозначных нелинейностей, существенно влияющих на качественные показатели си­стем управления. Применение классических приёмов для компенсации не­линейностей не эффективно в тех случаях, когда при эксплуатации систе­мы параметры нелинейности подвержены изменению;

• не рассмотрены особенности нечётких логических регуляторов за­ключающиеся в расширении функциональных возможностей связанных с повышением их интеллектуальности, что существенно расширяет область применения систем управления на основе нечёткой логики.

В данном пособии изложена необходимая информация для анализа и синтез проектируемых нечётких систем управления с использованием язы­ка инженерных вычислений Ма1;ЬаЬ. Приведена функциональная схема проектируемого нечёткого регулятора, описаны основные операторы, ис­пользуемые для моделирования их параметров, рассмотрены правила настройки, как лингвистических переменных, так и выбора вида и количе­ства нечётких термов.

Каждая глава пособия содержит большое количество примеров с ил­люстрацией результатов моделирования, а также комментариями по выбо­ру структуры и настройке параметров нечёткой системы управления.

При написании данного пособия авторы использовали как свои нара­ботки, так и опубликованные материалы других авторов, указанных в биб­лиографическим списке.

Глава 1. Основы теории нечётких множеств.

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

1. Основные соотношения булевой алгебры и теории нечётких множеств

В автоматике и в компьютерах всегда использовалась как математи­ческая основа алгебра логики, называемая также булевой алгеброй по имени её создателя английского математика Джорджа Буля (1815-1864). Математическая логика в её современном виде во многом базируется на том разделе математики, который называется теорией множеств.

Рассмотрим кратко основные определения математической логики, относящиеся к алгебре логики и теории множеств. В алгебре логики логиче­ские переменные а, Ь, с ... и логические функции А, В, С ... могут прини­мать только два значения, обозначаемые цифрами 0 и 1. Двум указанным значениям ставятся в соответствие различные взаимоисключающие собы­тия, условия, состояния логических устройств в реле, компьютерах. Например, да - нет, замыкание контакта - размыкание контакта, наличие сигнала - отсутствие сигнала. Цифры 0 и 1 и буквенные обозначения пе­ременных а, Ь, с ... в логике не числа, а символы, и алгебра логики - это алгебра состояний.

Л

Л

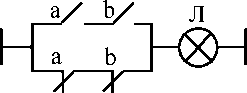
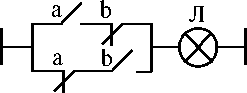1—7—<8Н

Рис. 1.1. Изображение логических схем: релейно-контактная

реализация:

а, б, в, г, д, е - операции И, ИЛИ, НЕ, импликации, эквивалентности,

неоднозначности соответственно а и б — контакты реле, Л - лампа

них являются следующие: Обозначение

а; 0а

а л Ь ; а ■ Ь ; а & Ь а V Ь ; а + Ь а ® Ь а « Ь а ® Ь

Операция

Отрицание, инверсия, НЕ Конъюнкция, И Дизъюнкция, ИЛИ Импликация, если а, то Ь Эквивалентность Неравнозначность

В логике имеется ряд операций. Наиболее употребительными из

Любую логическую операцию можно задать с помощью таблиц ис­тинности (табл. 1.1 задаёт операцию отрицания, табл. 1.2 - все другие пе­речисленные операции).

В простейшем случае, когда 0 - отсутствие сигнала, 1 - наличие сиг­нала, реализация логических операций может быть наглядно представлена в виде элементарных электрических контактных схем (рис. 1.1). Когда на

катушку реле (на рис. 1.1 не показана) подаётся напряжение, т.е. 1 (табл. 1.1, 1.2), то контакты срабатывают.

Таблица 1.1

a	0	1
a	1	0

Таблица 1.2

a	b	a л b	a v b	a ® b	a -—® b	a ® b
0	0	0	0	1	1	0
0	1	0	1	1	0	1
1	0	0	1	0	0	1
1	1	1	1	1	1	0

Алгебра логики, как и все алгебры, опирается на ряд аксиом (на ос­нове которых и построены таблицы истинности): а + b = b + а; а (b + с) = ab + ас; а + bc = (а + Ь)(а + с); а + а/a = а; а +( a) = b + b ; a ( a) = bb.

Так как любая переменная алгебры логики может принимать значе­ния только 0 или 1, то действительны также следующие выражения: 0 = Ï;

Ï =0; 0^0 = 0; Ы = 1; 0+0 = 0; 1+1 = 1; Ь0 = 0^1 = 0; 0+1 = 1+0 = 1.

В алгебре логики получен ряд законов. Приведём наиболее важные из них:

• нулевого множества - 0 • a • b •... • w = 0 ;

• универсального множества - 1 + a + b +... + w = 1;

• идемпотентности (тавтологии) - a • a •... • a = aⁿ = a и

a + a +... + a = n • a = a ;

• двойной инверсии - a = a ;

• дополнительности - a • a = 0 и a + a = 1;

• коммутативности - a • b = b • a и a + b = b + a ;

• ассоциативности- a •(b • c) = (a • b) • c = abc и a + (b + c) = (a + b) + c = a + b + c ;

• дистрибутивности - a •(b + c ) = ab + ac и a + bc = (a + b)a + c )

• закон де Моргана a • b •... • w = a + b + ... + w и a + b +... + w = a • b •... • w .

Обратимся теперь к элементарным основам теории множеств. В теории множеств используются следующие обозначения: множество А = {а, Ь,с}; е - элемент принадлежит множеству (например, у е А означает, что элемент у принадлежит множеству А; & - элемент не принадлежит множеству.

Задание множества выполняется в виде перечисления элементов или описанием. Перечисление задаётся списком: А = {а₁,а₂,...,а_п} или А = {а_г}, I =& I = {1,2,3,..., п}. Описание имеет вид: если Р - некоторое свойство про­извольного множества М, тогда А = {х е М / р(х)} - множество тех и только тех элементов х е М, которые обладают свойством Р. Например, если Р - свойство быть простым числом, то А = {х е N / р(х)} - множество всех про­стых чисел в множестве N.

В одноэлементном множестве А = {а, Ь, у} единственным элементом является множество {а, Ь, у}, состоящее из трёх элементов.

Множество А называется подмножеством множества В А с В ( - знак включения), если любой элемент; х е А принадлежит В. Если хотя бы один элемент А не принадлежит В, то А ё в. Если А с В и А ё В, то говорят, что А строго включается в В и записывают А е В, в противном случае А ё в, Множество А можно назвать подмножеством В, если А с В или А е В.

Пусть, например, В = {1, 2, 3} и А = {1, 3}, тогда А е В. Пусть В = {я,2,л/э,а}, А = {а,2} тогда А е В, а С = {а,2, {/э,а}} не содержится в В, так как элемент {/э ,а}, а следовательно, и С не являются элементами В.

Можно записать А = В, когда одинаковы все элементы множеств А и В (аксиома экстенсиональности). В противном случае А ё В. Число эле­ментов в множестве называется мощностью множества и обозначается |А| для множества А.

Если множество не имеет элементов, то оно называется пустым и обозначается 0. Мощность пустого множества | 0|.

Между множествами и их элементами могут существовать различ­ные отношения. Объединением (или суммой) двух, трёх и более множеств называется множество всех элементов, каждый из которых есть элемент хотя бы одного из данных множеств (слагаемых). Объединение мно-

п

жеств обозначается и. Например, и /' = 1, п

i=\

Пересечением двух, трёх и более множеств называется множество всех элементов, общих всем данным множествам. Пересечение двух не­пустых множеств может быть пустым. Пересечение множеств обозна-

п

чается п. Например, п /' = 1, п.

^а)

б)

А В

А В

м

Рис. 1.2. Венн-диаграмма для множеств А и В: а - АиВ; б - АпВ

Объединение и пересечение множеств пояснены так называемыми Венн-диаграммами (рис. 1.2). Пусть А является подмножеством основного множества X(А с X) и, например, А = {а₁₀,а_п,...,а₁₅} или А = {а_г}, где / е {10,11,...,15} Тогда можно записать так называемую функцию принадлеж­ности

/ ч Г1, если(х е А)

т а ^(х Н_{0 (£ А)};

[0, если(х £ А)

то есть m_A (x) = 1 в том случае, если

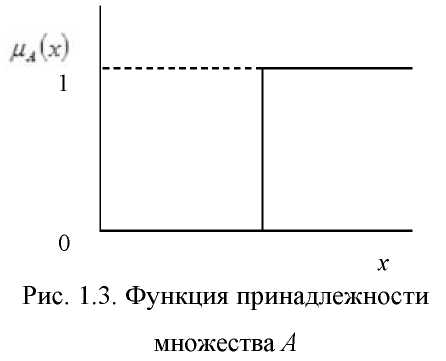элемент х принадлежит множеству А, и т_А (х) = 0 в том случае, если х не принадлежит множеству А.

Функция принадлежности в классической («чёткой») теории множеств может принимать, таким образом, два значения (рис. 1.3). На рис. 1.3 показано также пунк­тиром множество А - инверсия множества А или его дополнение.

2. Основные понятия нечётких множеств

Для нечётких множеств появляется возможность более подробного рассмотрения функции принадлежности. При использовании аппарата нечётких множеств (Fuzzy Set) в нечёткой логике (Fuzzy Logic) элемент множества может только частично принадлежать к данному множеству и частично принадлежать к любому другому множеству.

Теория нечётких множеств представляет собой расширение класси­ческой теории множеств. Она нечёткая, но ни в коем случае не неточная. Она организована и математически строго обоснована, как и классическая теория множеств, которая в ней содержится и является её частью. Для об­легчения понимания нечёткой теории множеств напомним, что человек, когда он размышляет, часто не считает правильным или просто не может принять решение: да или нет. Он принимает некоторое промежуточное решение: немного да или (и) немного нет. Вполне понятно, что между экс­периментальными величинами или состояниями: да и нет, истина и ложь, включено и выключено, один и ноль, - могут быть промежуточные со­стояния (величины), которые как раз и являются очень важными и очень нужными.

Любой элемент нечёткого множества может полностью принадле­жать некоторому нечёткому множеству (фаззи-множеству) или принадле­жать ему только в определённой степени. Поэтому может быть введена очень важная для нечётких множеств количественная мера - степень при­надлежности. При этом используются, как правило, только нормализо­ванные множества.

В нормализованном множестве (или нормальном множестве) степе­ни принадлежности всех элементов множества находятся (лежат) в диа­пазоне между 0 и 1:

т_А (х) е [0,1], т.е. тах т_А (^х) = 1, х е X , где Х- основное множество.

Рис. 1.4. Изображение чёткого множества А (а) и нечёткого множества В (б)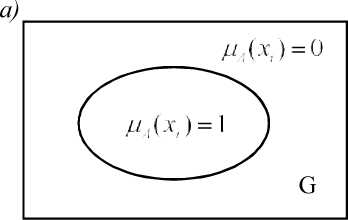

Для того чтобы получить нормализованное (нормальное) множе­ство, достаточно разделить все значения функции принадлежности на её максимальное значение. В дальнейшем будем рассматривать только нор­мализованные множества, максимальное значение функции принадлеж­ности т_А (х) = 1. Наглядное представление нормированных чёткого и не­чёткого множеств А и В, которые являются подмножеством основного множества О, дают Венн-диаграммы (рис. 1.4).

При введении математического понятия нечёткое множество в каче­стве наглядных примеров часто приводят обычное применение какого- нибудь обыденного понятия, категории. Например, типичное словесное

понятие юноша может моделироваться в виде, показанном на рис. 1.5.

ю

Любой элемент в определённом рассматриваемом множестве всегда

Рис. 1.5. Моделирование понятия юноша функцией принадлежности возраст р_возр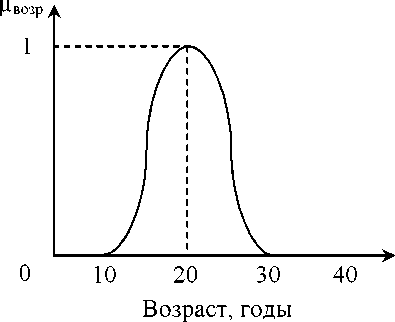

характеризуется его степенью при­надлежности. Запись вида т_А (^х) = 0,6 означает, что степень принадлежности х к множеству А составляет 0,6. При использовании лингвистических (сло­весных) обозначений можно записать для множества «Дорого» (предмет до­рого стоит в магазине):

т дорого {т^{елевизо}Р' 8опу") = °,85,

Рис. 1.6. Моделирование нечёткой функции принадлежности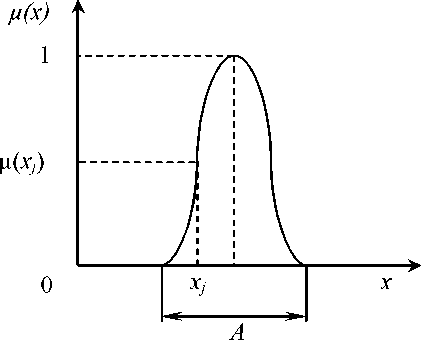

т_дорого(телевизорРекорд") = 0,2, т.е. сте­пень принадлежности для множе­ства «Дорого» для телевизора «Sony» составляет 0,85 (85 %), а для телевизора «Рекорд» 0,2 (20 %).

Форма изображения нечётко­го множества может быть различ­ной. Пусть А - нечёткое множество и - его элемент со степенью при­надлежности р*. Запись для множе­ства А может быть представлена в виде упорядоченных пар:

(1.1)

а = {(*!,т),(*2,т2)>•••} "х є о " х єG.

Здесь О - основное множество для элементов х (рис. 1.6), для упро­щения записи элемент х_г-, для которого степень принадлежности р = 0, опущен. Знак " - так называемый квантор общности. Запись "а читается

так: для всех а. Запись для множества А может быть представлена в более кратком виде:

^А = ^{(х; т а ^(х)) І^{х є} °) •

Рис. 1.7. Функция принадлежности множества «Приблизительно число 8»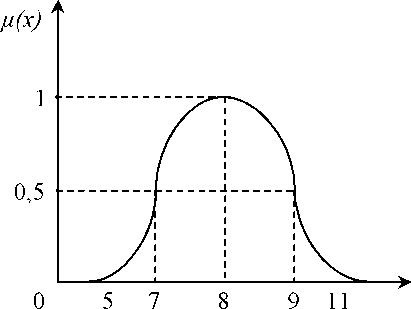

Г рафическое изображение

множества А, представлено на рис. 1.6.

Нечёткое множество строго определяется с помощью функции принадлежности. Можно предста­вить нечёткое множество, исполь­зуя аналитическую запись функции принадлежности. Рассмотрим такую запись на примере. На рис. 1.7 пока­зано множество А вещественных чисел и нечёткая функция принадлежно­сти «Приблизительно равно числу 8». Нечёткое множество записывается в виде

^А = ^; Аа ^{(х ) 1} Аа ^{(х )}=¹ + ^{(х -8)4 ]1} [

Это довольно характерный для нечёткой логики случай. Как видим, числа 7 и 9 принадлежат нечёткой функции принадлежности «Приблизи­тельно восемь» только со степенью принадлежности 0,5: т_А (х = 7)= т_А (х = 9)= 0,5, а число 13 - со степенью принадлежности ноль: т _А (х = 13)= 0. Заметим, что в обыденной жизни часто нельзя, например, определить, каков точно возраст ребёнка: 8, 9 или 11 лет. Вот эту инфор­мацию и отражает функция принадлежности на рис. 1.7.

Элемент х)■ может принад­лежать к нескольким множе­ствам. Случай, когда элемент принадлежит одновременно к двум множествам А и В, показан на рис. 1.8.

Рис. 1.8. Элемент хі, принадлежащий двум нечётким множествам А и В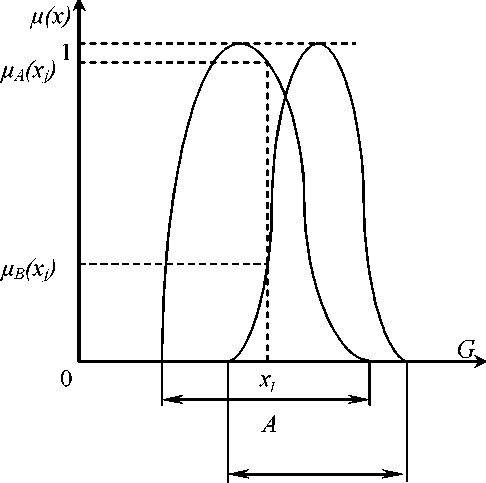

Возможен и другой вид за­писи нечёткого множества А. Его можно представить в виде сово­купности пар: А = [ц_А (х)/х | х е о}.

Эта запись в общем виде аналогична предыдущей. Но её легче пред­ставить для одного, единичного значения множества. Такое множество, со­стоящее только из одного значения, получило название синглетон (или син- глет). Синглетон может быть записан, например, в виде т_А (х_к)/х_к (рис. 1.9). Носителем такого множества является отдельная точка - элемент множе­ства О. Поэтому любое множество А можно представить как интеграл

А = |Аа (х)/х, "е о,

а при конечном числе элементов (п) и как сумму:

а = т ⁽*) ^/ *1 + т (*2) ^{/ х}2 + •••+а п ^(хп^{) / х}п = Е т ^(х,^{) /} х, ^, = ^1,2,..., ^п.

Здесь, разумеется, нет действия деления - это только вид записи множества А через его функции принадлежности, каждая из которых представляет собой синглетон.

Цл(х) ^м 1 -

0

Пусть основное множество соответ­ствует множеству возможных значений высоты уровня сыпучего материала в бун­кере от 0,2 м (пустой) до 4 м (полный). Вы-

Хк

Рис. 1.9. Единичное значение

сота уровня материала измеряется с дискретным шагом 0,1 м, поэтому функция принадлежности также задаётся в дискретном виде. Нечёткое множество А, соответствующее нечёткому словесному (лингвистическому) понятию «Пустой бункер», может быть представлено по выражению (1) в виде

А = {(0,1; 1), (0,2; 1), (0,3; 0,7), (0,4; 0,45), (0,5; 0,18), (0,6; 0,1), (0,7; 0,2), (0,8; 0), (0,9; 0)}.

Из этого примера видно, что понятие пустой бункер полностью от­вечает обыденному восприятию. Если заглянуть в бункер, то заметим: при отметке 0,2 м и ниже - устройство разгрузки бункера полностью покрыто материалом, через 30 см на отметке 0,5 м уже только 18 % площади этого сечения бункера заполнено материалом, а на отметке 0,6 м - 10 % (у сте­нок), а выше материала нет.

Функции принадлежности

Таблица 1.3

Наименование функции	Аналитическая формула
1	2
Функция принадлежности в виде разности между двумя сигмоидными функциями	их)~ 1 - 1 ^ ' \+Є^а1(х-с1) 1+е-а2Іх-с2)

Продолжение табл. 1.3

1	2
Двухсторонняя гауссовская функция принадлежности	если С]< т(х)=- если С]> т (х)=	'С2, то ехр(х - с1)2/(- 2ц )2 ) х < с 1, с < х < с2 ехр(х - с2 )2/(- 2а2 )2 ) х > с2 С2, то ехр((х - с1 )2/ (- 2а1 )2), х < с2 ехр((х - с1 )2 /(- 2а1 )2 )• ехр((х - с2 )2 /(- 2а2 )2) с2 < х < с1 ехр((х - с2 )2 /(- 2а2 )2) х > с1
Симметричная гауссовская функция принадлежности	(X - Ь )2 т (х)=е 2 с2
Обобщенная колокообразная функция принадлежности	т(х ) =	1
		1 +	х - С а	2Ь
Пи-подобная функция при­надлежности	произведение ^-подобной и г-подобной функций

Произведение двух сигмоид­ных функций принадлежно­сти	т (х) 1 + е ~а1 (х-С1) 1 + е а2 (х-С2)
Сигмоидная функция при­надлежности	т (х )= ( ч 1 1 + е -а (х-С)
^-подобная функция принад­лежности	' V ' II	х < а аппроксимация, а < х < Ь х > Ь
Трапециевидная функция принадлежности	р.{х) =	г 0, х < а х — а - , а < х < Ъ Ь — а 1, Ь<х<с с — х г, с < х < й с — а < 0, й < х
Треугольная функция при­надлежности	р.{х) =	г 0, х < а х — а - , а < х < Ъ Ь — а Ъ — х , Ъ < х < с Ь — с < 0, с < х
7-подобная функция принад­лежности	' V ' II	1, х < а аппроксимация, а < х < Ь 0, х > Ь

3. Соотношения и операции в нечёткой логике

Покажем, как выполняются операции объединения, пересечения и др. с чёткими и нечёткими множествами.

Пусть А, В - нечёткие нормализованные множества; ^_А(х), ^_в(х) - сте­пени принадлежности элемента х к нечётким множествам А, В; х - рас­сматриваемый элемент; G - множество всех элементов х, основное мно­жество; - минимум-оператор (из фигурных скобок выбирается

элемент с минимальным значением); тах{...} - максимум-оператор (из фи­гурных скобок выбирается элемент с максимальным значением).

Отметим, что операции с множествами: объединение множеств, пе­ресечение множеств, а также операции дополнения множества, - можно поставить в соответствие с операциями алгебры логики. Если А и В - мно­жества, то объединению А и В соответствует операция дизъюнкции (см. табл. 1.2) avb, пересечению множеств АпВ — операция конъюнкции алЬ, а так называемому дополнению множества A в алгебре логики соот­ветствует инверсия а (см. табл. 1.1). Рассмотрим эти операции с множе­ствами. Объединение множеств

A и B = {(х); mauв (х)} - ^Vx е G,

где множество G - основное (универсальное) множество, т.е. множество всех элементов х.

Подробнее объединение множеств А и В можно записать в виде

^{A и в} =^{(х); m Аив^(х) I m aub ^(х) > ^{о} Vx е G, (1}.¹

^гд^е maub ^{(х) :}= ^max{mа ^(х) mв^(х)}, "х е g .

Знак := означает по определению равно; в более подробной записи АиВ свойство m_Аив (х)> 0 указывает на то, что носителем 8(А) этого мно­жества является тот элемент х, степень принадлежности которого больше нуля:

х е з (а) о т _А (х) > о, где о — знак эквивалентности.

Рассмотрим объединение множеств для чёткой и нечёткой логики.

1. Пусть х е с и х е В, где С и В - чёткие множества; т_с(х) = 1; т_В (х) = 0 . Степень принадлежности т_сиВ (х) = тах{т_с (х); т_В (х)}=шах(1;0)=1, что означает х е с и В .

Этот же результат для а V Ь получаем на основе таблицы истинности (см. табл. 1.2).

2. Пусть 0={а, Ь, с, й, е, /, к} - основное множество; А={(а; 0,7), (с; 0,3), (й; 0,2), ([; 0,5), (к; 0,1)} и В={(Ь; 1), (с; 0,6), (В; 0,7), (е; 0,2)}

- нечёткие множества. Тогда

АиВ={(а;0,7), (Ь; 1), (с;0,6), (й;0,7), (е;0,2), ([;0,5), (к;0,1)}. Пересечение множеств записывается в виде

^{А п В} = (^(х); тАпБ ^(х)}, "^{х е} °

или подробней

^{А П В} = ^{х; ВапБ ^(х) I ВапБ ^(х)>^о}. "^{х е С , (3)}

^гд^е тапв ^{(х) :}= ^шш{та ^(х); тв ^(х)} "^{х е} °.

Рассмотрим пересечение множеств для чёткой логики. Здесь воз­можны два случая:

1. хе С и х е в; С, В - чёткие множества. Пусть т_с (х) = 1, т _В (х) = 0. Пересечение Цсг_В(х) = тт{и_с(х);т_в(х)} = тт{1;0} = 0, что означает х £ С п В ²

Обратимся к пересечению нечётких множеств. Пусть G = {a, b, c, d, e} - основное множество; A={(a;0,7),(c;0,3),(d;0,2)} и

B={(b;1),(с;0,6),(d;0,7),(е;0,2)} - нечёткие множества.

В пересечении A о B = {(c;0,3), (d;0,2)} элементы а, b, с отсутствуют, так как они содержатся не в обоих множествах, а только в одном: например, для элемента b m_A (b)= 0 , m_B (b)= 1. Тогда m_AoB (b) := min{m_A (b) m_B (b)} = min{0,1} = 0.

Для дополнения множества можем записать

^A = fe m_A ^(b))} Vx e G . (4)

При нормированном множестве (см. рис. 1.3) т_A (х) := 1 - т_А (х) Ух е G. Рассмотрим два случая:

1. С и D - чёткие множества; х е C, т_с (х) = 1. Следовательно, т_с (х) := 1 - т_с (х) = 1 -1 = 0, что означает х £ C .

2. х е D, т_D (х) = 0. Следовательно, т_О (х) := 1 - то (х) = 1 - 0 = 0, что означает х е О.

Пусть 0={а, Ь, с, а} - основное нечёткое множество;

С=((а;0,5),(с;0,1),(ё;1)}. Известно, что С = {(х;т_с (х)) | т_с (х) = 1 - тс (х)}.

Тогда С = {(а;0,5), (с;0,1), (<2;0)}, причём т_с (а)= 0 означает d £ С и может быть опущено. Итак, С = {(а;0,5) (с;0,9)}.

Произведение двух множеств

А X В = ^{(х; т_Л,Б^(х))^}, Ух е G , ^гд^е т ахв ^{(х) :}= т а ^{(х )}т в ^{(х), Ух е G}.

Алгебраическое произведение двух множеств А и В можно предста­вить и в виде конъюнкции. Например, если О = {а, Ь, с, а, е, /},

А={(а;0,7),(с;0,5),(А;0,2),(/;0,5)}, а В={(Ь;1),(с;0,6),(А;0,7),(е;0,2)}, то А х В = {(с;0,18), (а;0,14)}. Здесь элементы а, Ь, е, /выпали, так как они в обоих множествах не содержатся. Например, для элемента Ь т _А (Ь) = 0, т _в (Ь) = 1, следовательно, т _Ахв (х) = т _А (х)т _в (х) = 0 1 = 0.

Логическая сумма двух множеств

^А + ^в =^{(х; та+в ^(х))} ^, "х е о,

^{где т}А+в ^(х) = ^тА ^(х) + ^тв ^(х) ^{— т}А ^(х)^тв ^(х) , "^{Х е 0} •

Логическую сумму А+В можно записать в виде дизъюнкции. Пусть 0={а,Ь,с,А,е}, А=((а;0,7),(с;0,3),(А;0,2)},

В={(Ь; 1), (с; 0,6), (А; 0,7), (е; 0,2)}. Тогда А + в = {(а; 0,7); (Ь;1) (с;0,72) (А ;0,7б); (е;0,2)}

Покажем вычисления для элемента с подробней:

На (с)+тв (^с)—та (^с)тв (с)=0,3+0,6—0,3 • 0,б = 0,72.

Отметим, что законы нечёткой логики отличаются от законов чёт­кой (классической) логики. Для нечётких множеств 0={а,Ь},

А={(а;0,7)} и в = А ={т_А (а)}={(1 — т_А )}={(а;0,3)}, произведение

А х в = А х А = т_АтА = 0.7 • 0.3 = 0.21 ф 0, тогда как в булевой алгебре в соответ­ствии с законом дополнительности А х А = 0 .

Очень часто и другие законы нечёткой логики отличаются от законов чёткой логики. Между логическими операциями И, ИЛИ, НЕ, когда они применяются к множествам и когда они применяются в алгебре логики, име­ется различие. В первом случае, когда операторы используются для мно­жеств, результат получается также в виде множества. Во втором случае опе­ратор связывает или действует на наблюдаемые элементы с определёнными свойствами и в результате получаем также элемент. Так, например, множе­ство импортных телевизоров связано операторами с множеством крупно­экранных телевизоров. В конце преобразований получаем опять множество, а именно множество телевизоров импортных, крупноэкранных.

Для элементов множеств, например, свойство «дорогой» одного те­левизора (предположим, «Sony») связано с качеством «крупноэкранный». В результате получаем вновь один телевизор, например, с качествами «до­рогой» и «крупноэкранный» (предположим, «Sony», 82 см по диагонали).

4. Переменные, функции и операции в нечёткой

логике

В нечёткой логике даже в одних и тех же ситуациях, при идентич­ных начальных условиях (в том числе производственных, технических) при вычислениях для одной и той же логической операции могут выби­раться различные операторы.

Исследования в области нечёткой математики продолжаются, и в ближайшее время можно ожидать новых успехов, а пока тот или другой оператор выбирается на основе сравнения результатов его применения, т.е. в зависимости от того, даёт ли использование того или другого опера­тора удовлетворительное решение задачи. Кроме того, выбор оператора зависит от имеющихся в распоряжении вычислительных мощностей, спе­цифики проблем и интуиции, опыта разработчика. Выбор того или друго­го оператора должен оправдываться достижением цели.

Рассмотрим применение операторов в логических операциях.

Конъюнкция — И. Для этой операции существует несколько операторов, из которых важнейшими являются следующие:

1. минимум-оператор m_{A Л B} (х ) = min {m_A (х ); fi_B (х )};

2. оператор «произведение» m_{A Л B} (х ) = ji_A (х )m_B (х)

Каждый из этих операторов имеет свою специфику, своё «поле деятельности». Чаще других используется минимум-оператор.

Пусть степени принадлежности нечётких множеств А и В соответ­ственно m_A (х) = 075; (х) = 0.85. Запишем решение для операторов 1 и

2: соответственно m_Av в (х) = min{0.75;0.85}= 0.75.

Для оператора 2: ji_A,,_B (х) = m_A (х = 0 75)m_B (х = 0.85)= 0.75 • 0.85 = 0.6375

Как видно из примера, результаты применения операторов 1 и 2 от­личаются на 11 %. Поэтому при выборе того или другого оператора следу­ет учитывать специфику задачи.

Легко также проверить, что для чёткой логики (например, при m _А (х) = m _в (х) = 1 результаты будут соответствовать таблице истинности, т.е. будут одинаковы для всех операторов.

Для операции И, как и для пересечения множеств, во многих случаях применяются минимум-операторы, поэтому эти два отношения множеств чаще всего совпадают.

Дизъюнкция - ИЛИ. Для этой операции также установлено несколько операторов. Перечислим важнейшие:

1. максимум-оператор m_{Av в} (х) = max{m_A (х); т_в (х)};

2. mAv в^(х)=тА^(х)+тв^(х) - тА ^(хК^(х);

3. mAv в^(х)=^min{l; ⁽mA^(х)+тв^(х))}.

В этом случае - для операции ИЛИ - также каждый из операторов следует использовать в определённых ситуациях, и выбор данного опера­тора для подобных задач должен быть подтверждён опытом. Для опера­ции ИЛИ, как и для объединения множеств, во многих случаях использу­ется максимум-оператор, поэтому эти два отношения множеств чаще всего совпадают.

В повседневных размышлениях человек чаще всего использует не строгие операции И, ИЛИ, но некоторые другие, которые имеют проме­жуточные свойства и находятся между этими двумя операциями. Суще­ствуют такие компенсирующие, «смягчающие» суждения «да» (1) и «нет» (0), а следовательно, смягчающие и результаты операции операторы у и X. Операция компенсации с оператором X:

тллв ^(х)=Амл ^(хК ММ¹ - ¹1мл ^(х)+тв ^(х)-т_л ^(хК ^(х)], при я є[о,і].

Для Я = о получаем операцию ИЛИ:

тляв^(х) 1я=о=тл^(х)+тв^{(х) -} т_А ^(х К^(х)=т_А, в^(х); для Я = 1 операцию И:

тляв^(х) 1я=1 = тл ^(хК^(х)=тллв^(х);

Операция компенсации с оператором у:

т_Л1в^(х)=\мл^(х К^{(х )}І^{-7 [1 -[1 -} тл^{(х )}]^{[1 -} тв^{(х )]}Г^{, п}р^и у ^^[о,1],

При у = 0 получаем операцию И

тл₁в^(х) у=о = тл^(х К^(х)=т_{А л} в^(х); при у = 1 - операцию ИЛИ

тлв^(х) у=о=^{1 -[1 -} тл^{(х )][1 -} тв^(х)]=т_А ^(х)+тв^{(х) -} т_А ^(х К^(х)=т_А,в^(х)

Гамма-оператор может быть использован и с различными весо­выми коэффициентами (степенями): для множеств А и В

т_Л1в (*)=\та ⁽*Г тв ⁽* Г ^{] 71} -I¹ - т_А ^(х ГI¹ - тв ^(х Г I

при о < т_А (х); т_в (х)< 1, о < у < 1; за > о, зв > о; за + зв = 1.

Операция отрицания —

Рис. 1.10. Функция принадлежности множества А и его дополнения Л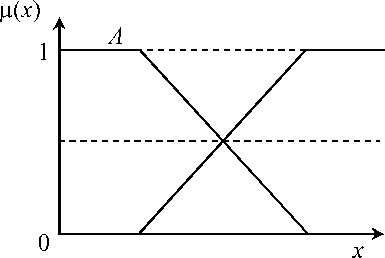

НЕ. Эта операция соответ­ствует операции дополнения для чёткого (см. рис. 1.3) и не­чёткого множеств. Для нечётко­го множества значения функ­ции принадлежности

т_А (х) = (х) = 0,5 являются цен­

тральным значением (рис. 1.10) и чаще всего т_А (х) и т_А (х) принимают симметричные значения относительно 0,5. Операция отри­цания может применяться и для нелинейных функций принадлежности.

Расширенное определение этой операции производится с примене­нием оператора (коэффициента) р: т_А (х) = [1 - т_А (х)]^р, р > 0.

ПРИМЕР 1. В магазине продаются телевизоры типа «Рекорд»: один в деревянном корпусе под красное дерево (экран 57 см), другой в чёрном пластмассовом корпусе (69 см), третий в сером пластмассовом корпусе (49 см). Для покупки проводится поиск одного телевизора в красивом корпусе и с большим экраном. При этом качества «красивый» и «большой экран» равнозначны.

Решение. Для телевизора в деревянном корпусе качество «краси­вый» выполнено полностью, но качество «большой экран» только частич­но. Запишем функции принадлежности для предлагаемых телевизоров и определим конъюнкцию множеств «красивый» и «большой» с помощью шт-оператора в табл. 1.4.

Таким образом, больше других подходит к множеству «красивых» и с «большим экраном» телевизор в деревянном корпусе. Отметим, что вы -

ражение больше других подходит - это обыденное выражение людей - не­чёткие множества и нечёткая логика ближе к обыденному, а не к матема­тическому мышлению.

Таблица 1.4

Телевизор в корпусе	m КРАС	^БОЛЬШ	m КРАСиБОЛЬШ
деревянном	1	0,6	0,6
пластмассовом :
чёрном	0,4	0,6	0,4
сером	0	0,2	0,2

В классической логике для нашего примера множество «красивых крупноэкранных» телевизоров было бы пустым множеством, так как оба качества «красивый» и «большой экран» одновременно не выполняются. Математическая строгость не соответствует таким, например, рассуждени­ям: «Да, конечно, экран 57 см - это не слишком большой экран, но краси­вый корпус так украсит комнату и можно согласиться на этот телеви­зор». Нечёткая логика позволяет учесть эти человеческие оценки и, что очень важно, придать им формализованную математическую форму, что необходимо в сложных многокомпонентных задачах.

Нулевой результат для телевизора в сером корпусе еще раз под­тверждает, что классическая логика содержится в нечёткой логике как её раздел (этот телевизор абсолютно не принадлежит искомому множеству).

ПРИМЕР 2. С целью лучшего выполнения заданных в примере 1 требований согласимся, чтобы искомый телевизор был бы «не на 100 % красивым и не на 100 % крупноэкранным», т.е. будем считать возможным допустимость нестрогого подхода, что полностью соответствует поста­новке нашей повседневной задачи и введём компенсирующий оператор. Пусть 1 = 0.8 .

Решение. Обозначим для краткости записи множество красивый - А, множество большой экран - В, переменную телевизор - х.

Тогда для телевизоров в деревянном, чёрном и сером корпусе соот­ветственно по формуле (5)

т_АВ (*) = 0.8(1 ■ 0.б)+(1 - 0.8)[1 + 0.6 -1 ■ 0.6] = 0.68;

т_АВ (*) = 0.8(1 ■ 0.4)+(1 - 0.8)[1 + 0.4 -1 ■ 0.4] = 0.52; т_А1В (х) = 0.8(0 ■ 0.2)+(1 — 0.8)[0 + 0.2 - 0 ■ 0.2] = 0.04.

Сравним результаты вычислений без компенсирующего, «сглажи­вающего» требования покупателя оператора X и с этим оператором: в пер­вом случае отношение для телевизоров с деревянным и черным корпусом 0,6/0,4=1,5, во втором 0,68/0,5=1,36; аналогично для телевизоров с де­ревянным и серым корпусом 0,6/0=¥ и 0,6/0,04=15.

Значения отношений сблизились. Если с телевизором с серым кор­пусом, который в 15 раз меньше «подходит» покупателю, все ясно, то между двумя другими телевизорами различие невелико, хотя закономер­ность та же.