1.2. Режим холостого хода

Режимом холостого хода (ХХ) электрической цепи, называется такой ее режим функционирования, при котором величина сопротивления нагрузки стремиться к бесконечности, а величина тока, протекающего через нагрузку, стремиться к нулю.

В приведенном определении по существу содержатся необходимое и достаточное условия, характеризующие собой режим холостого хода.

Используя определение режима холостого хода , и применяя закон Ома для полной цепи (1), напишем аналитическое выражение для тока в анализируемом режиме :

Проводя аналогию с раннее рассмотренным режимом короткого замыкания, можем записать аналитическое выражение для мощности источника ЭДС в режиме холостого хода:

Применение такой методики позволяет составить аналитическое выражение для мощности, выделяющейся на нагрузке в рассматриваемом режиме :

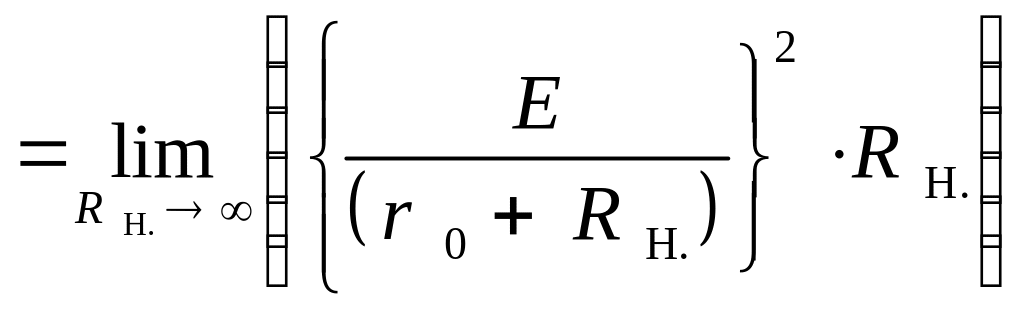
Аналитическое выражение для мощности потерь - мощности, выделяющейся на внутреннем сопротивлении источника ЭДС, имеет вид:

.

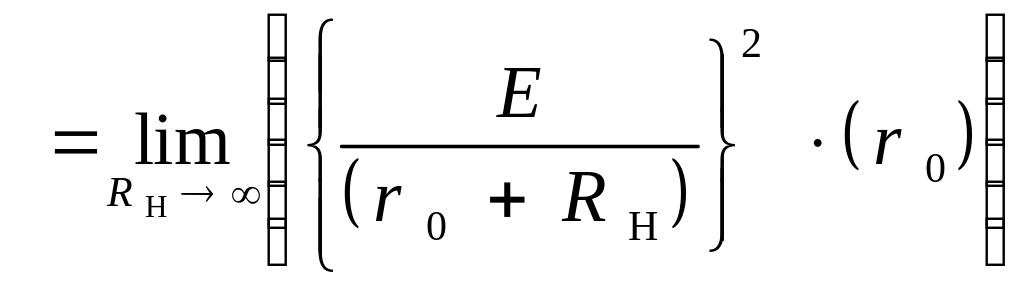
Применяя соотношения (1.2.2) и (1.2.3), находим значение мощности источника ЭДС в режиме холостого хода:

.

Физическое содержание полученного значения соотношения (1.2.5) состоит в следующем: если в режиме ХХ величина сопротивления нагрузки бесконечно большая, что соответствует разомкнутой (обрыву) ветви, содержащей нагрузку, то ток в рассматриваемой цепи, равен нулю, а поэтому равна нулю и мощность, вырабатываемая источником электродвижущей силы.

Определим значение мощности потерь на внутреннем сопротивлении самого источника ЭДС:

.

Применение закона Джоуля – Ленца, позволяет записать аналитическое выражение для мощности, выделяющейся на нагрузке в режиме холостого хода :

.

Для анализа соотношения (1.2.7) целесообразно воспользовавшись следующими теоремами, известными читателю из курса дифференциального исчисления, вот эти теоремы: о нахождении предела произведения, вычислении предела дроби, о нахождении предела степени:

.

Итак, в соотношении (1.2.8) получается неопределенность следующего вида: 0·∞.

Раскроем эту неопределенность двумя способами. Первый способ раскрытия неопределенности вида 0·∞ математический. Из курса математического анализа известно, что неопределенность указанного вида, раскрывается с помощью метода сведения этой неопределенности к неопределенностям следующих видов: .

Другими словами, необходимо, свести к одному из указанных видов неопределенностей, неопределенность, полученную нами в соотношении (1.2.8):

.

Полученное соотношение (1.2.9) представляет собой неопределенность требуемого нам вида, а именно вида: .

Полученную неопределенность можно так же раскрыть следующими двумя методами.

Оба этих метода относятся к математическим методам. Первый метод это метод раскрытия неопределенности видов: с использованием правила Иоганна Бернулли – Лопиталя .

Напомним кратко математическую сущность правила Иоганна Бернулли - Лопиталя. При определении предела непрерывной функции часто, в результате подстановки предельного значения аргумента этой функции, приходят к неопределенностям следующих видов:

.

Нахождение предела функции в таких случаях называют раскрытием неопределенности. Теорема, которая приводится ниже, исторически известная под правилом Лопиталя, представляет собой математический базис, позволяющий раскрывать указанные выше две первые неопределенности, т. е, неопределенности вида: . Справедливости ради, необходимо отметить, что маркиз де Лопиталь был единственным учеником у выдающегося швейцарского математика Иоганна Бернулли. Именно благодаря Иоганну Бернулли, маркиз де Лопиталь получил систематические сведения о тогда еще новом направлении в математике – анализе бесконечно малых.

В последствие, из этого ученья возникло стройное, логичное, гармоничное направление математики, получившие название – математический анализ. Математический анализ объединяет в себе два направления: дифференциальное и интегральное исчисление.

Следует отметить, что маркиз де Лопиталь тщательно законспектировал лекции и в последствие издал их отдельной книгой, в виде первого учебника по дифференциальному исчислению в Европе: это историческое событие произошло в 1696 году, когда маркиз Лопиталь выпускает в Париже под своим именем первый в истории учебник под названием: «Анализ бесконечно малых для исследования кривых линий» (на французском языке), в основу этой книги была положена первая часть конспекта Иоганна Бернулли.

Именно в силу того обстоятельства, что Лопиталь был учеником Иоганна Бернулли, историки математики, стали правило Лопиталя называть правилом И. Бернулли – Лопиталя. Ниже приводится формулировка теоремы, которая иллюстрирует собой правило И. Бернулли – Лопиталя.

Теорема.

Если существуют две функции , такие, что для них выполняются следующие условия:

т.е., когда обе рассматриваемые функции непрерывны и дифференцируемые,

то предельные значения этих функции соответственно равны:

,

а отношения этих функций имеют следующий вид:

то тогда указанные неопределенности можно раскрывать по правилу И.Бернулли - Лопиталя:

Приведенная нами выше теорема остается в силе и в том случае, если ее условие , будет заменено на условие :

т.е., теорему можно применять к раскрытию неопределенностей вида .

Во всех условиях этой теоремы предел можно понимать как односторонний. Эта теорема справедлива так - же для односторонних пределов и в случае, когда предельное значение варианты , т.е., обозначает собой также и бесконечность.

Применим к выражению , взятому из ранее полученного соотношения (1.2.7), правило И.Бернулли - Лопиталя, в результате этого, найдем:

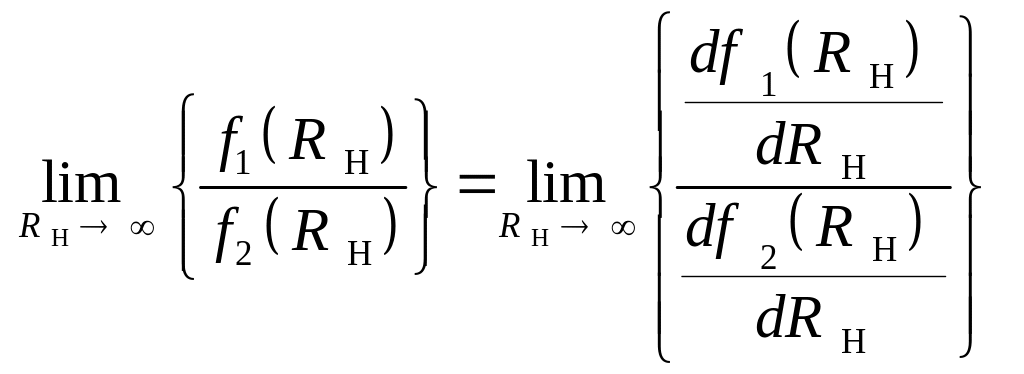
В записанном соотношении , соответствующие функции ,

равны:

Выполнив процедуру дифференцирования каждой из указанных функций,

получим:

Тогда, применение правила И.Бернулли - Лопиталя к соотношению , позволит раскрыть указанную выше неопределенность :

Приведем еще один математический метод , позволяющий раскрывать неопределенности вида .

В соотношении до выполнения предельного перехода осуществим тождественные преобразования над выражением, находящимся под знаком предела. Используя формулу сокращенного умножения для квадрата суммы

двух чисел , мы получим:

Тогда, выражение, стоящее под знаком предела, будет иметь следующий

вид:

До осуществления предельного перехода, выполним процедуру деления выражения, стоящего под символом предела в соотношение , на наивысшую степень варианты R²_н, после этого получим:

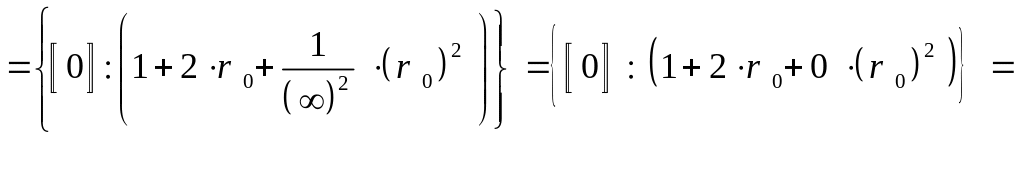
Сопоставляя результат выражения с результатом выражения, приходим к выводу, что они равны между собой.

Укажем, кроме того, еще один метод раскрытия полученной неопределенности.

Этот физический метод основан на применение второго закона Кирхгофа, который непосредственно вытекает из закона сохранения энергии.

В силу применения второго закона Кирхгофа имеем:

Умножая левую и правую часть соотношения (1.28) на значение тока холостого хода, получим:

Принимая во внимание полученные нами ранее соотношения (1.2.3) и (1.2.4), в силу которых:

можем переписать соотношение (1.29) в равносильном виде:

Используя записанное соотношение, найдем, следуя физическому подходу, величину мощности нагрузки в режиме ХХ.

Из соотношения (1.2.10), находим мощность в нагрузке для режима ХХ:

.

Все три метода, примененные к раскрытию неопределенности вида , дали один и тот же результат.

Определим КПД для режима холостого хода (ХХ).

По аналогии с соотношением (1.1.20) запишем выражение, определяющее :

.

Полученное соотношение , с математической точки зрения, представляет собой удвоенную неопределенность, возникшую в результате осуществления предельного перехода, т.е., при нахождении предела от аналитического выражения, которое определяет собой КПД для режима холостого хода, который математически компактно можно записать следующим образом .

В числителе последнего соотношения удвоенная неопределенность возникла вследствие того, что, когда величина резистивного элемента, представляющего собой линейную нагрузку, безгранично возрастает, т.е., когда , то тогда вместе с этим безгранично уменьшается величина тока в цепи, т. е, имеет место выражение .

Раскрывать удвоенную неопределенность, можно с помощью тождественных преобразований, выполняющимися над выражением, стоящим под символом предела .

.

Осуществив предельный переход в полученном выражении, найдем значение КПД для рассматриваемого режима:

Определим, геометрический характер зависимости с целью дальнейшего построения соответствующего графика. Для этого выполним процедуру деления “уголком“ следующего выражения:

Выполнив процедуру предельного перехода в последнем соотношении (1.2.14), найдем числовое значение КПД цепи, функционирующей в режиме ХХ:

Выводы по режиму холостого хода (ХХ):

1) в режиме ХХ рассматриваемая нами линейная электрическая цепь

имеет максимальное значение КПД, численно равное единице;

2) аналитически геометрический характер зависимости подчиняется гиперболическому закону (рис. 3);

Общий вывод для двух ранее рассмотренных режимов КЗ и ХХ.

Рассматриваемая линейная электрическая цепь, как в режиме КЗ, так и в режиме ХХ, имеет одинаковые значения для мощности в нагрузке .

Режим холостого хода рассмотрен в данной лекции с учетом того, что этот режим широко использовался в курсе «Электротехника и электроника».

Данный режим использовался, как при рассмотрении опыта по испытанию трансформатора, так и при исследовании частотных характеристик реактивных элементов, входящих в состав последовательного колебательного контура, с одной стороны, так и при исследовании амплитудно – частотной и фазо – частотной характеристик контура, с другой стороны.

В лекциях по дисциплине “Электроника“ режим ХХ так же получил свое применение, там в частности, он используется в методе эквивалентного генератора, служащего для расчета электронных схем, функционирующих в линейном режиме. Метод эквивалентного генератора будет более подробно изложен ниже в данном пособии, чем это представлялось в уже прочитанном лекционном курсе: в частности, будет приведено его

теоретическое обоснование, осуществлен численный анализ одной из линейных цепей постоянного тока, который реализуется по этому методу.

Следует так же отметить, что частотные методы широко используются при анализе систем связи, которые рассматриваются в курсе “Автоматизированные системы управления и связь“, читаемом в академии МЧС ГПС РФ.